





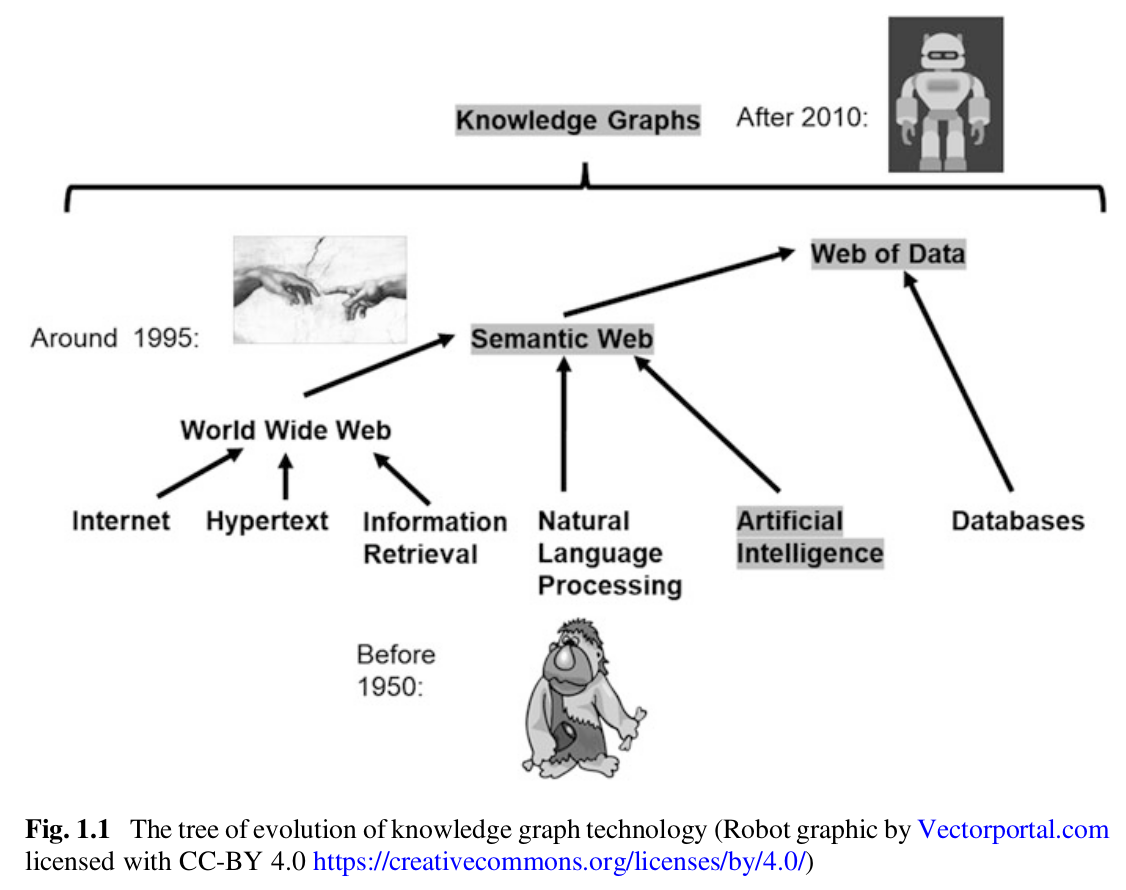




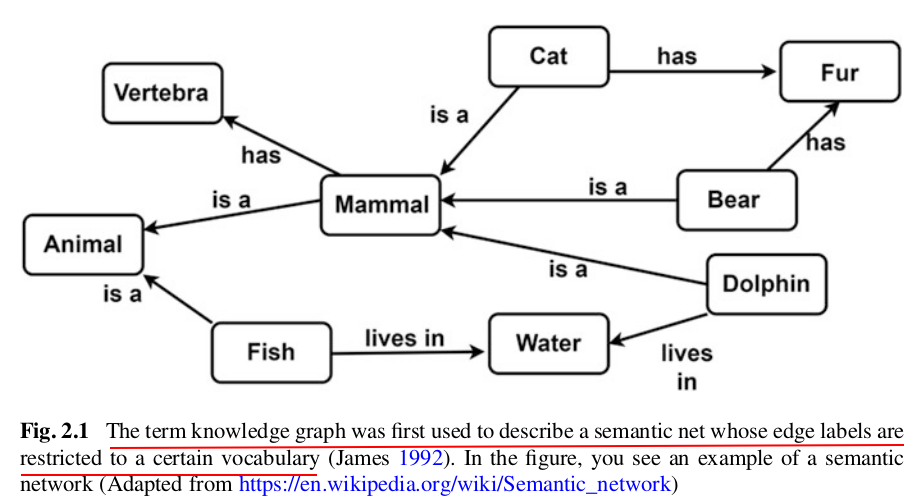

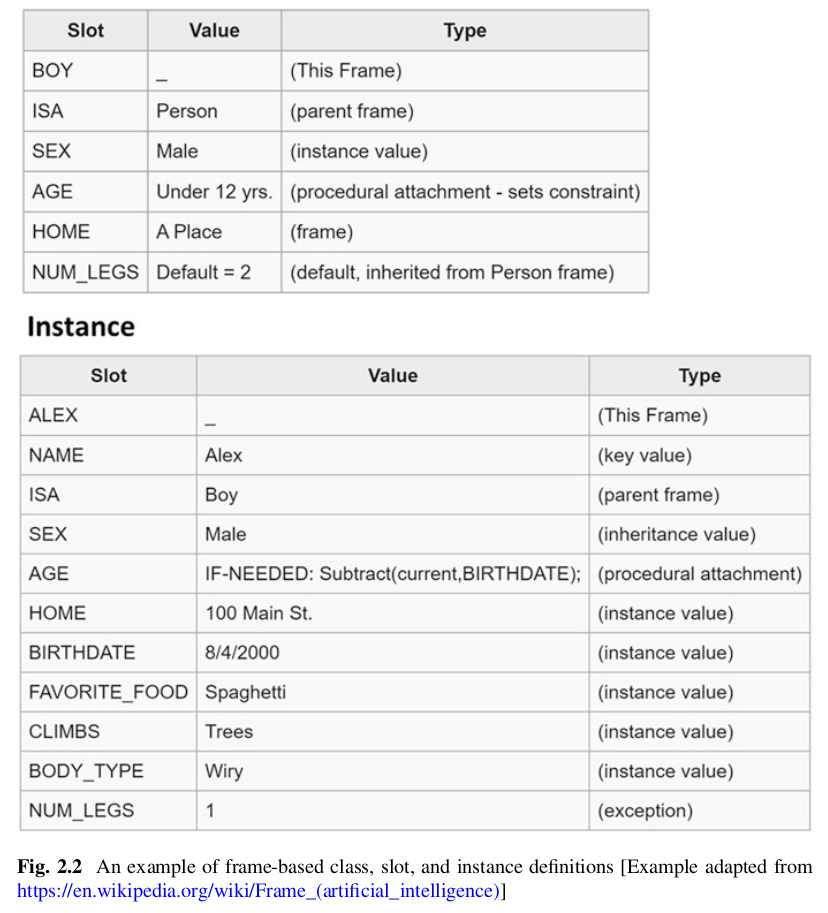




First-order logic (FOL), also known as predicate logic, is a formal system used in mathematics, philosophy, computer science, and linguistics to represent and reason about propositions and their relationships.
Key Features of First-Order Logic:
-
Variables and Quantifiers:
-
Variables (e.g., x, y) stand for objects in a domain.
-
Quantifiers allow statements about "all" or "some" objects:
-
Universal quantifier (∀x): "for all x"
-
Existential quantifier (∃x): "there exists an x"
-
-
-
Predicates:
-
Predicates represent properties or relationships between objects.
-
For example,
Loves(x, y)might mean "x loves y".
-
-
Logical Connectives:
-
¬ (not), ∧ (and), ∨ (or), → (implies), ↔ (if and only if)
-
-
Constants and Functions:
-
Constants represent specific objects (e.g.,
a,b, orJohn). -
Functions map objects to objects (e.g.,
fatherOf(x)returns the father of x).
-
-
Domain of Discourse:
-
The set of objects that variables refer to. All quantifiers range over this domain.
-
Example in FOL:
"Everyone loves someone":
∀x ∃y Loves(x,y)
This means: for every person x, there exists a person y such that x loves y.
Why It's Important:
-
First-order logic is powerful enough to express most of classical mathematics.
-
It underpins many areas in artificial intelligence, especially knowledge representation and automated reasoning.
Horn logic is a special subset of first-order logic (and propositional logic) that's widely used in logic programming, databases (like Datalog), and artificial intelligence.
Key Concept:
A Horn clause is a clause (a disjunction of literals) with at most one positive literal.
Types of Horn Clauses:
-
Definite clause (exactly one positive literal):
-
Example:
A←B1∧B2∧⋯∧BnThis means: If B₁ and B₂ and ... and Bₙ are true, then A is true.
-
This is commonly used as a rule in logic programming.
-
-
-
Fact (a definite clause with no conditions):
-
Example:
AAASimply states that A is true.
-
-
Goal clause or query (no positive literal):
-
Example:
←B1∧B2∧⋯∧BnUsed in proving or querying (i.e., "is this condition derivable?").
-
Example in Prolog-like Syntax:
loves(mary, john). % Fact happy(X) :- loves(X, john). % Rule (Horn clause) ?- happy(mary). % Query (goal)
Why Horn Logic Is Important:
-
It enables efficient reasoning and deduction (e.g., via forward chaining or backward chaining).
-
It forms the foundation of logic programming languages, such as Prolog.
-
Unlike general first-order logic, reasoning with Horn clauses is decidable and efficient in many cases.




The expression:
is written in Description Logic (DL), a formalism used in knowledge representation (like in OWL ontologies). Let's break it down:
Symbols and Meaning
-
Bachelor: A class (concept) we're defining.
-
≡: Equivalence — the left-hand side (Bachelor) is equivalent to the right-hand side.
-
¬: Negation (NOT).
-
∃married.⊤: There exists a relation married to anything (⊤ means "top", i.e., any individual).
-
⊓: Conjunction (AND).
-
Man: A class (concept) representing men.
Step-by-step Interpretation
-
∃married.⊤: The individual is married to someone (exists a "married" relation with any individual).
-
¬∃married.⊤: The individual is not married to anyone.
-
¬∃married.⊤ ⊓ Man: The individual is a man AND not married to anyone.
Full Interpretation
Bachelor ≡ ¬∃married.⊤ ⊓ Man
A Bachelor is exactly a man who is not married to anyone.
This is a formal way of defining the concept of a bachelor in terms of logic: a person who is a man and has no marriage relationship.





























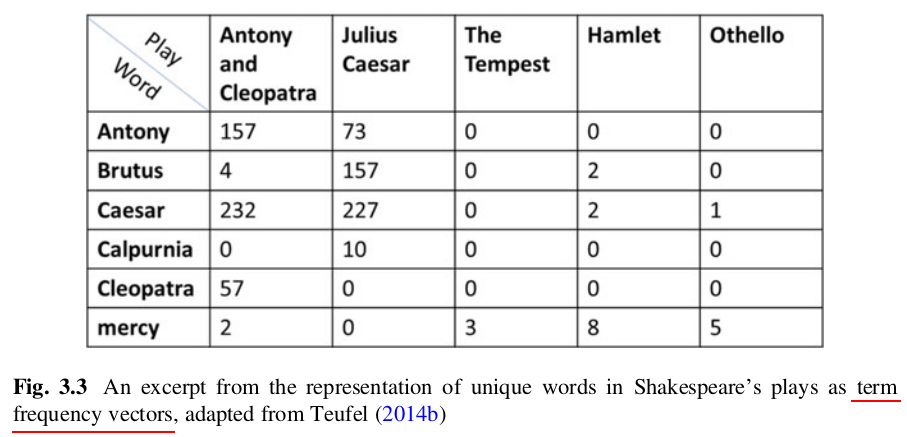


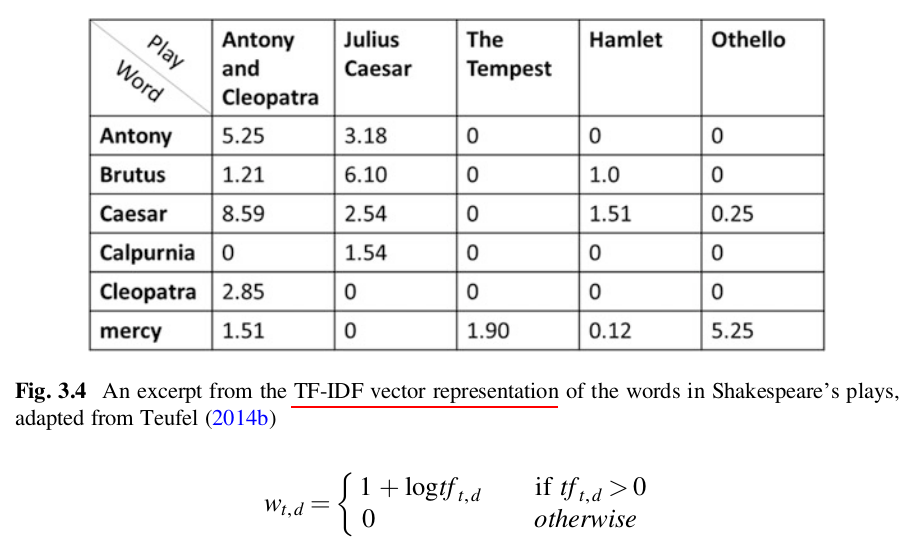 TF-IDF
TF-IDF



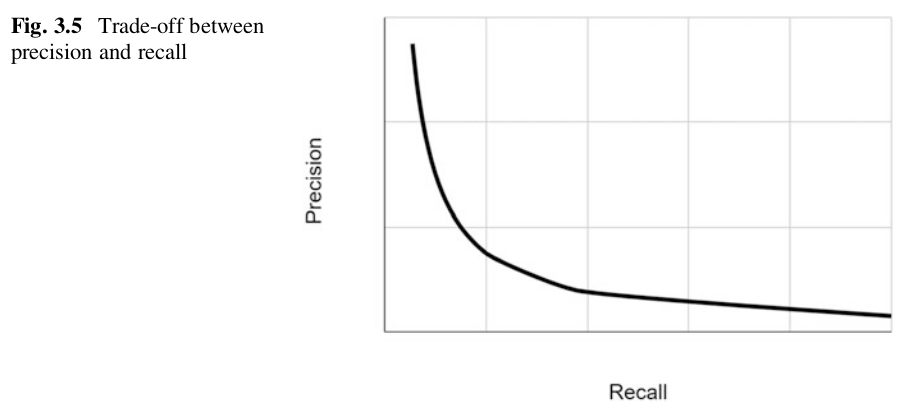



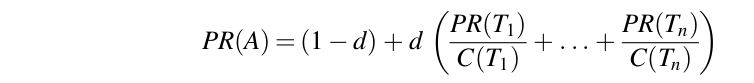
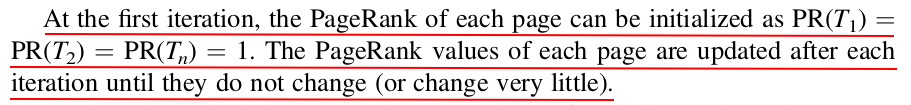

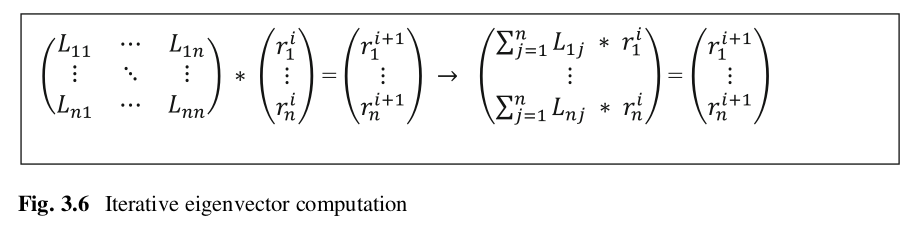 Why this iterative computation can get the eigenvector?
Why this iterative computation can get the eigenvector?

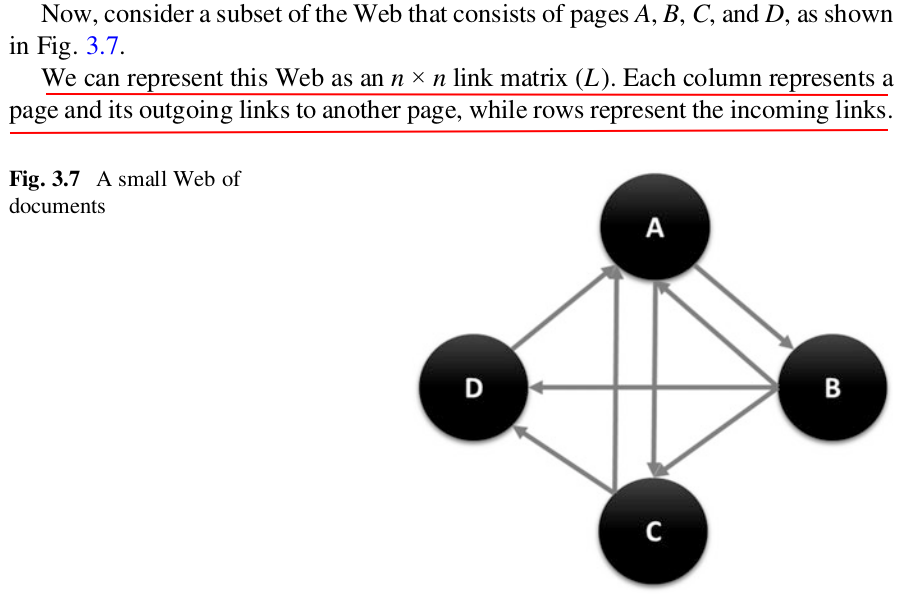


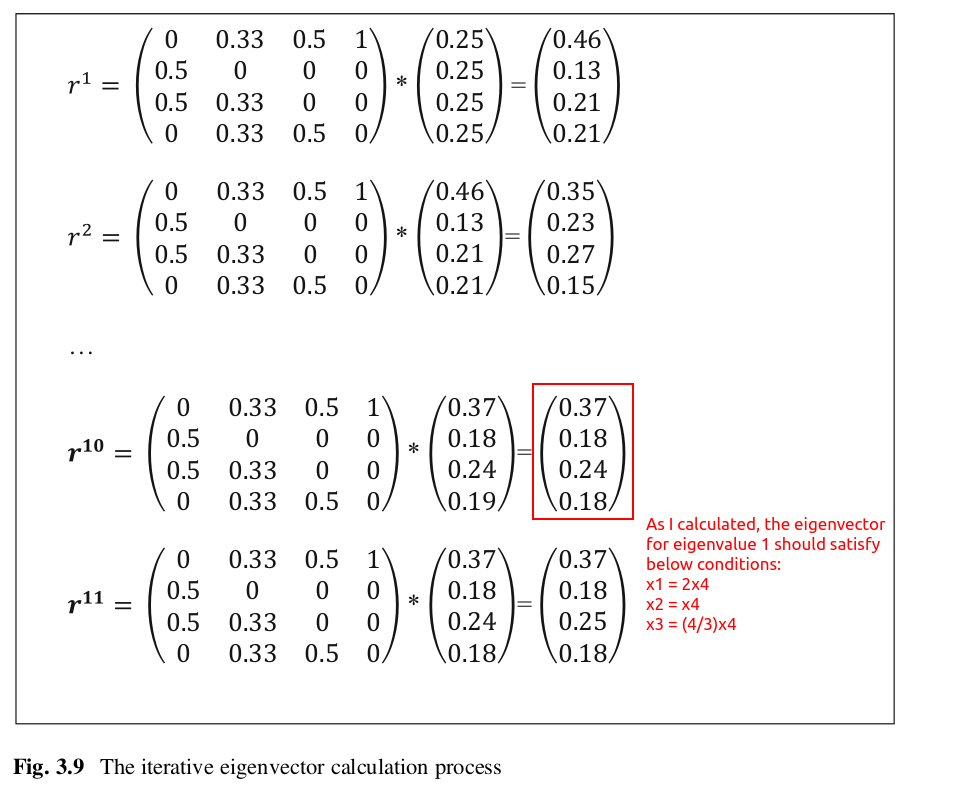











 浙公网安备 33010602011771号
浙公网安备 33010602011771号