LeetCode - Max Points on a Line

Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.

 

Example 1:

Input: points = [[1,1],[2,2],[3,3]]
Output: 3

Example 2:

Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4

 

Constraints:

• 1 <= points.length <= 300
• points[i].length == 2
• -104 <= xi, yi <= 104
• All the points are unique.

 

My Solution:

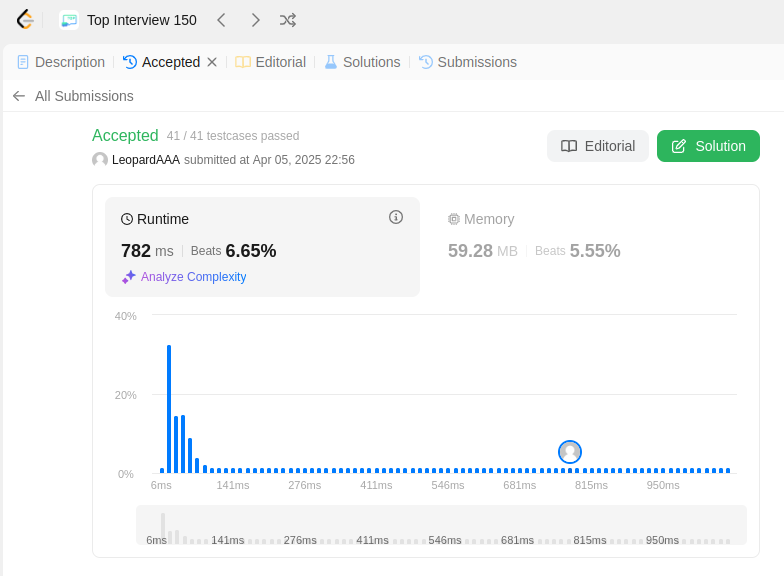
import numpy as np
from collections import defaultdict


class Solution:
    def maxPoints(self, points: List[List[int]]) -> int:
        n = len(points)
        if n <= 2:
            return n
        
        def solve_equation(point1, point2):
            #  y1 = k * x1 + b  -->  x1 * k + b = y1
            #  y2 = k * x2 + b  -->  x2 * k + b = y2

            # Coefficient Matrix (A)
            A = np.array([[point1[0], 1],
                          [point2[0], 1]])
            
            # Right-hand side (B)
            B = np.array([point1[1], point2[1]])

            # Solve Ax = B
            solution = np.linalg.solve(A, B)

            return tuple(solution)
        
        kb_dict = defaultdict(set)

        for i in range(n - 1):
            for j in range(i + 1, n):
                if points[i][0] == points[j][0]:
                    k, b = float('inf'), points[i][0]
                elif points[i][1] == points[j][1]:
                    k, b = 0, points[i][1]
                else:
                    k, b = solve_equation(points[i], points[j])
                    k, b = round(float(k), 8), round(float(b), 8)
                kb_dict[(k, b)].add(tuple(points[i]))
                kb_dict[(k, b)].add(tuple(points[j]))
        
        max_points = 0
        print(kb_dict)
        for v in kb_dict.values():
            max_points = max(max_points, len(v))
        
        return max_points

 

 

ChatGPT's Solution:

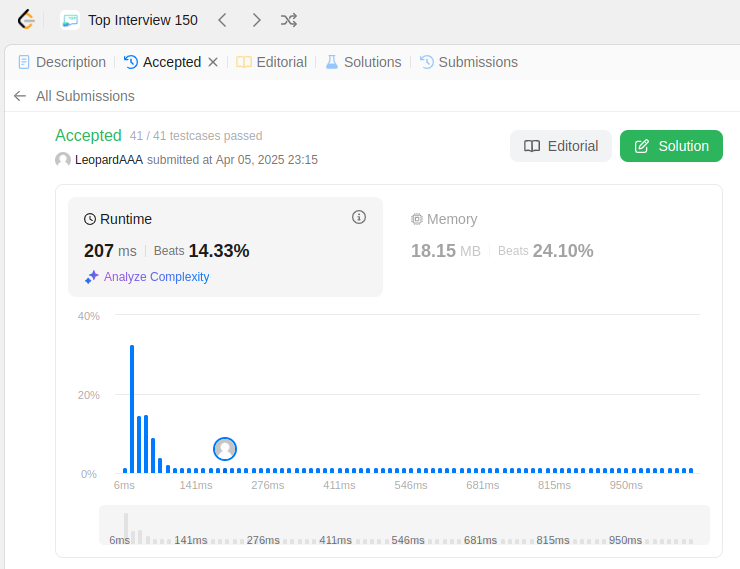
from collections import defaultdict
from fractions import Fraction


class Solution:
    def maxPoints(self, points: List[List[int]]) -> int:
        n = len(points)
        if n <= 2:
            return n
        
        max_points = 0

        for i in range(n):
            slopes = defaultdict(int)
            cur_max = 0

            for j in range(i + 1, len(points)):
                x1, y1 = points[i]
                x2, y2 = points[j]

                if x1 == x2:
                    slope = 'inf'  # Vertical line
                else:
                    slope = Fraction(y2 - y1, x2 - x1)
                
                slopes[slope] += 1
                cur_max = max(cur_max, slopes[slope])
            
            # Add 1 for the anchor point itself
            max_points = max(max_points, cur_max + 1)
        
        return max_points

 

 

Do we need to consider the intercept?

No, not in this specific problem.
Here’s why:

We're trying to find how many points lie on the same straight line, and for that, we're:

• Choosing each point i as an anchor.

• Calculating the slope between i and every other point j.

If two points share the same slope with the same anchor point, then they must lie on the same line passing through that anchor — no need to check intercepts.

⚠️ Intercepts do matter when:

• You are comparing global lines (not from a fixed anchor).

• But in this problem, you're always measuring from the current point i, so slope is enough.