LeetCode - Word Search

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

 

Example 1:

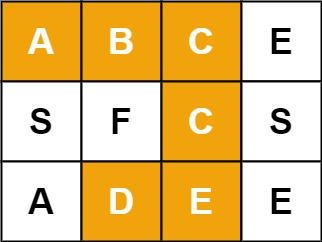
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

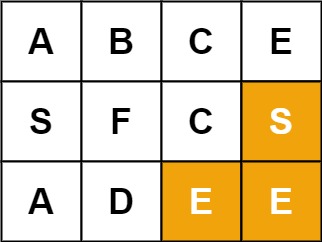
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

 

Constraints:

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board and word consists of only lowercase and uppercase English letters.

 

ChatGPT's Solution:

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        if not board:
            return False
        
        rows, cols = len(board), len(board[0])

        def backtrack(r, c, index) -> bool:
            if index == len(word):
                return True
            if r < 0 or r >= rows or c < 0 or c >= cols or board[r][c] != word[index]:
                return False
            
            # Mark the cell as visited by modifying the board temporarily
            temp, board[r][c] = board[r][c], '#'

            # Explore all possible directions
            for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                if backtrack(r + dr, c + dc, index + 1):
                    return True
            
            # Restore the cell back to its original state
            board[r][c] = temp

            return False
        
        for r in range(rows):
            for c in range(cols):
                if board[r][c] == word[0] and backtrack(r, c, 0):
                    return True
        
        return False