LeetCode - N-Queens II

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

 

Example 1:

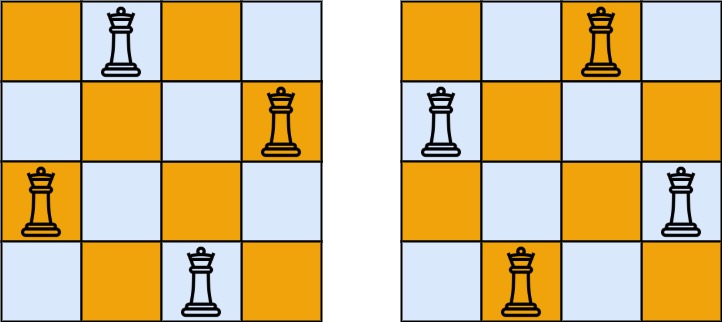
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1
Output: 1

 

Constraints:

• 1 <= n <= 9

 

ChatGPT's Solution:

class Solution:
    def totalNQueens(self, n: int) -> int:
        def backtrack(row: int, cols: set, diag1: set, diag2: set) -> int:
            if row == n:
                return 1
            
            count = 0
            for col in range(n):
                if col in cols or (row - col) in diag1 or (row + col) in diag2:
                    continue
                
                cols.add(col)
                diag1.add(row - col)
                diag2.add(row + col)

                count += backtrack(row + 1, cols, diag1, diag2)

                cols.remove(col)
                diag1.remove(row - col)
                diag2.remove(row + col)
        
            return count
        
        return backtrack(0, set(), set(), set())

 

 

This implementation:

• Uses backtracking to explore valid queen placements.

• Utilizes sets to track column and diagonal attacks.

• Recursively places queens row by row.

• Counts valid board configurations.

 

                if col in cols or (row - col) in diag1 or (row + col) in diag2:
                    continue

 

Understanding the Constraints

In chess, a queen attacks:

1. Vertically (same column)

2. Diagonally (both main and anti-diagonals)

Breaking Down the Condition

This condition checks whether placing a queen at (row, col) is valid.

1. col in cols

   • Checks if another queen is already placed in the same column (col).

   • If col is in the cols set, it means another queen is already in that column, so we skip this placement.

2. (row - col) in diag1 (Main diagonal: \)

   • This checks if another queen exists on the same main diagonal.

   • The main diagonal is identified by row - col, because all cells on the same diagonal share this value.

   • Example:

     • (0,0), (1,1), (2,2) all have row - col = 0

     • (1,0), (2,1), (3,2) all have row - col = 1

3. (row + col) in diag2 (Anti-diagonal: /)

   • This checks if another queen exists on the same anti-diagonal.

   • The anti-diagonal is identified by row + col, because all cells on the same diagonal share this sum.

   • Example:

     • (0,3), (1,2), (2,1) all have row + col = 3

     • (1,3), (2,2), (3,1) all have row + col = 4

Effect of continue

If any of these conditions are met, the current column is unsafe, so we continue to the next column.