LeetCode - Word Search II

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

 

Example 1:

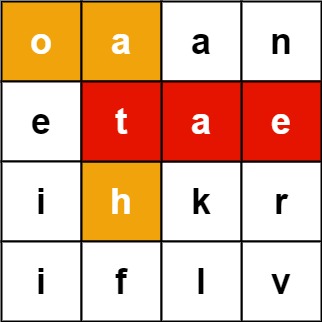
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

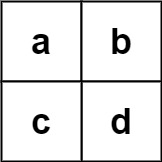
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

 

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 104
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

 

ChatGPT's Solution:

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_word = False


class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        # Build Trie from words
        def build_trie(words):
            root = TrieNode()
            for word in words:
                node = root
                for char in word:
                    if char not in node.children:
                        node.children[char] = TrieNode()
                    node = node.children[char]
                node.is_word = True
            return root
        
        # Backtracking DFS function to search for words
        def dfs(board, node, i, j, path):
            # Check boundaries and if current position is already visited or doesn't match
            if i < 0 or j < 0 or i >= len(board) or j >= len(board[0]) or board[i][j] == '#':
                return
            
            char = board[i][j]
            if char not in node.children:
                return
            
            # Mark the cell as visited
            board[i][j] = '#'

            node = node.children[char]
            path += char

            # If we found a valid word, add it to the result
            if node.is_word:
                result.add(path)
            
            # Explore the 4 adjacent cells
            dfs(board, node, i + 1, j, path)
            dfs(board, node, i - 1, j, path)
            dfs(board, node, i, j + 1, path)
            dfs(board, node, i, j - 1, path)

            # Un mark the cell for the next exploration
            board[i][j] = char
        
        # Main part of the algorithm
        trie_root = build_trie(words)
        result = set()

        for i in range(len(board)):
            for j in range(len(board[0])):
                dfs(board, trie_root, i, j, '')
        
        return list(result)

 

 

Explanation:

1. TrieNode Class: A basic Trie node that stores the children nodes and a boolean flag is_word to mark if the node represents the end of a word.

2. build_trie(): Builds a Trie from the list of words.

3. dfs(): Performs Depth-First Search (DFS) to explore adjacent cells on the board. If the current cell matches the next character of a word, the search continues. If a complete word is found, it's added to the result set.

4. Main Loop: The main function iterates over the board, and for each cell, calls dfs to search for words starting from that cell.