LeetCode - Populating Next Right Pointers in Each Node II

Given a binary tree

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

 

Example 1:

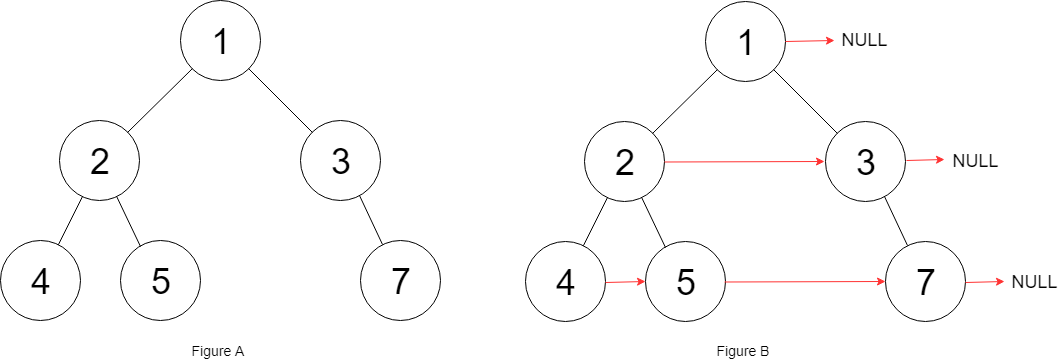
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

 

Constraints:

• The number of nodes in the tree is in the range [0, 6000].
• -100 <= Node.val <= 100

 

My Solution:

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root or not root.left and not root.right:
            return root
        
        if root.right:
            next_node = root.next
            while next_node:
                if next_node.left:
                    root.right.next = next_node.left
                    break
                elif next_node.right:
                    root.right.next = next_node.right
                    break
                
                next_node = next_node.next
            
            if root.right.left or root.right.right:
                root.right = self.connect(root.right)
        
        if root.left:
            if root.right:
                root.left.next = root.right
            else:
                next_node = root.next
                while next_node:
                    if next_node.left:
                        root.left.next = next_node.left
                        break
                    elif next_node.right:
                        root.left.next = next_node.right
                        break
                    
                    next_node = next_node.next

            if root.left.left or root.left.right:
                root.left = self.connect(root.left)


        return root

 

 

ChatGPT's Solution:

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""


from collections import deque


class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return None
        
        queue = deque([root])

        while queue:
            level_size = len(queue)
            prev = None

            for _ in range(level_size):
                node = queue.popleft()

                if prev:
                    prev.next = node
                prev = node

                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            
            # Last node in level should point to None
            prev.next = None
        
        return root

 

 

Explanation:

1. Use BFS (level-order traversal) with a queue:

   • Start with the root node.

   • Process nodes level by level.

   • Connect each node’s next pointer to the node on its right.

2. Maintain a prev pointer:

   • It tracks the previous node at the same level.

   • The last node in a level should point to None.

 

What is a deque?

A deque (short for double-ended queue) is a data structure that allows fast appends and pops from both ends (front and back). It’s part of Python's collections module and is ideal for situations where you need to efficiently perform operations at both ends of the sequence.

Key Operations of deque:

1. append(x)

   • Adds an item x to the right end (back) of the deque.

   • Time complexity: O(1)

2. appendleft(x)

   • Adds an item x to the left end (front) of the deque.

   • Time complexity: O(1)

3. pop()

   • Removes and returns the item from the right end (back) of the deque.

   • Time complexity: O(1)

4. popleft()

   • Removes and returns the item from the left end (front) of the deque.

   • Time complexity: O(1)

5. extend(iterable)

   • Adds all elements from the iterable to the right end of the deque.

   • Time complexity: O(k), where k is the number of items being added.

6. extendleft(iterable)

   • Adds all elements from the iterable to the left end of the deque. The elements are added in reverse order.

   • Time complexity: O(k)

7. rotate(n)

   • Rotates the deque n steps to the right (if n is positive) or left (if n is negative).

   • Time complexity: O(k), where k is the number of elements in the deque.