GAN笔记

  • 如果一个变量相对于另一个变量的条件熵为0，即H(Y|X)=0，则等价于两个变量有函数关系
  • 如果一个随机变量的熵为0，即H(X)=0，则它只有一种可能的情况

Introduction

生成式对抗网络(Generative Adversarial Networks, GAN)是一种在2014年被提出的一种网络结构：《Generative Adversarial Networks》

那什么是GAN呢，可以用一个经典的故事来讲解GAN的原理：有一团伙G(Generator)专门生产假钞，生产后的假钞花出去后在市场上流通，还有一个政府部门D(Discriminator)专门来辨别市场上流通钞票的真伪。团伙G想让自己生产的假钞能够以假乱真，而政府部门D为了保持市场稳定就必须尽可能的将市场上的假钞给挑出来，这样团伙G和政府部门D就在对抗博弈中不断提高自己的能力。

GAN的结构：GAN的里面有两个神经网络，一个是生成器(Generator)，一个是判别器(Discriminator)。生成器将自己生成的数据和真实数据混合在一起后送给判别器，生成器生成后的数据通过传给判别器后获得判别器的反馈来优化自己的生成能力，提高自己生成数据被判别器判断成真实数据的概率。判别器通过对生成器生成的数据和真实数据进行分类来优化自己的判断能力，提高自己识别数据是来自生成器还是真实数据的能力。

那团伙G和政府部门D是如何提高自己的能力的呢，假设政府部门D一天专门研究市场上最新的假钞以此提高自己的防伪技术，一天专门去市场上应用自己的最新防伪技术识别假钞；而团伙G一天专门生产假钞在市场上购买物资，一天通过研究政府部门D的最新防伪技术提升自己。

图1 Step1：Update Discriminator

这样第一天团伙G生产了一堆假钞拿到市场上去购买物资，而此时政府部门通过研究市场上流通的假钞来提高自己的防伪技术。第二天团伙G发现自己生产的假钞总能被识别出来，就开始研究政府部门最新的防伪技术来防止自己生产的假钞被识别出来。以此循环往复，团伙G和政府部门D在这个博弈中都不断提高自己的能力。

图2 Step2：Update Generator

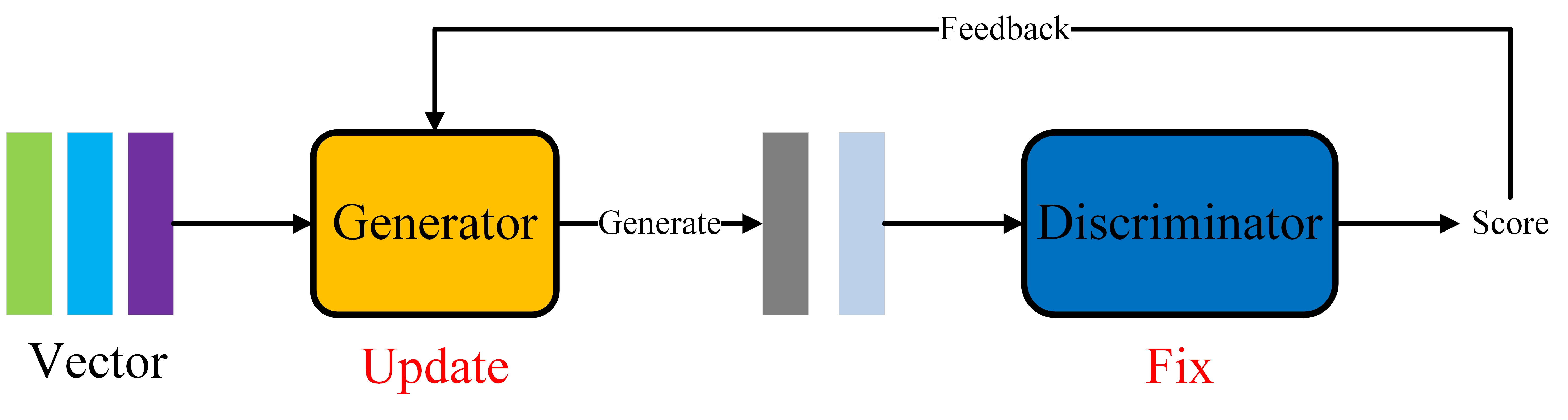
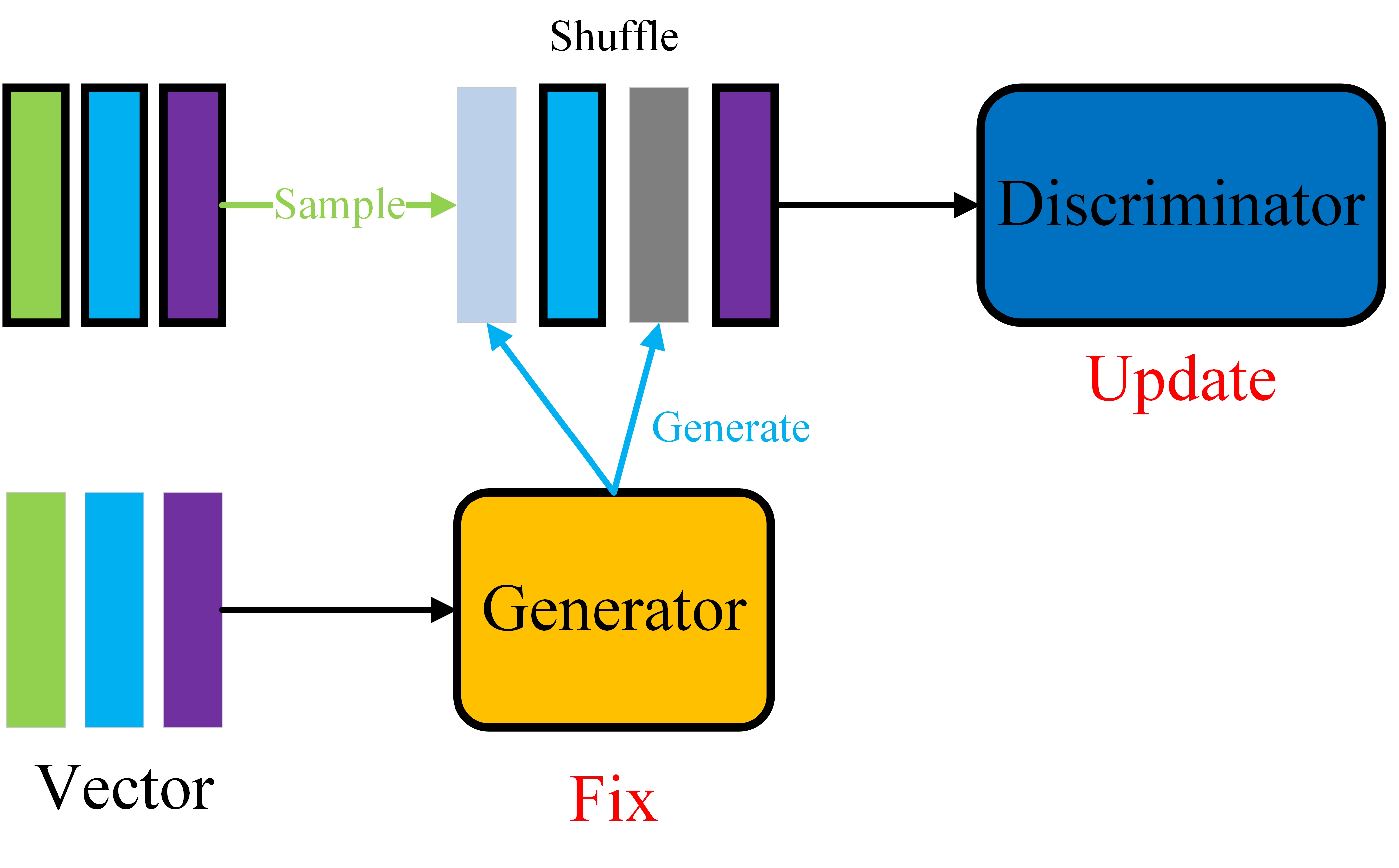
GAN的训练方法：

  1. 第一步：如图1，固定住生成器的参数，将生成器生成的数据同真实数据混合起来送给判别器并更新判别器的参数
  2. 第二步：如图2，固定住判别器的参数，将生成器生成的数据来送给判别器，并通过判别器的反馈来更新生成器的参数

GAN里面的判别器最后训练出来了并没有什么实际的应用价值，它只能用于判断生成器的数据和真实数据的区别，所以GAN最终的训练目的是训练一个很好的生成器来生成数据，而且对于现在的生成模型来说，GAN应该算是生成效果最好的模型了。

Generative Adversarial Networks

原始的GAN

用数学化的语言描述一下GAN：假设真实数据服从一个\(P_{data}\)的概率分布，而GAN的生成器生成的数据服从一个\(P_G\)的概率分布，GAN的目的就是通过生成器和判别器的博弈使\(P_G\)无限趋近于\(P_{data}\)，那么GAN的优化目标就是减小概率分布\(P_G\)和\(P_{data}\)之间的差异，而divergence通常就用于衡量两个概率分布之间的差异性，那么我们的真实目标其实是去减小\(P_G\)和\(P_{data}\)之间的divergence，即Generator的公式就是：

\[G = \arg{\min_G{Div(P_G, P_{data})}} \]

然而在现实情况中，对于一个连续概率分布的divergence通常是很难算出来的，在GAN中使用了一个方法来近似\(P_G\)和\(P_{data}\)之间的divergence。

生成器的问题先放一下，先来说说判别器的优化目标，判别器的目标是尽可能正确地将数据中来自\(P_G\)和\(P_{data}\)的数据区分出来，我们设送入判别器的数据为\(y\)，则判别器的判断结果为\(D(y)\)，则对于一个二分类的神经网络的Loss Function是其分类结果的交叉熵函数，即对于判别器的优化目标是最小化Loss Function，也就是最小化交叉熵函数：

\[D = \arg{\min_D{\frac{1}{N}\sum_{i=1}^{N}{-[P_{data}log{D(y)} + P_Glog(1-D(y))]}}} \]

上面的公式就是交叉熵函数公式，那么判别器其实是要尽可能地区分来自\(P_G\)和\(P_{data}\)的数据，那我们对交叉熵求其最小值就等价于求负交叉熵的最大值，并将其改写为期望的形式，所以上面的公式等价于（注意在D中其目标函数为\(V(D,G)\)）：

\[D = \arg{\max_D{V(D, G)}} = \arg{\max_D{E_{y \sim P_{data}}[logD(y)] + E_{y \sim P_G}[log(1-D(y))]}} \]

现在回到上面的\(P_G\)和\(P_{data}\)之间的divergence无法求解的问题，在原论文中经过推导之后发现\(\max_{D}{V(D,G)}\)与JS divergence相关，所以我们可以用\(\max_{D}{V(D,G)}\)来近似\(P_G\)和\(P_{data}\)之间的divergence，由此来解决这个问题，所以G的目标函数就是（注意在G的目标函数中\(\max_DV(D,G)\)为一个Loss Function，G的目标就是最小化这个Loss Function，这里\(\arg{\min_G}\)意思是最小化Loss Function，这里的\(min\)和后面的\(max\)表示的意思不同，第一次看这个公式容易误解）：

\[G = \arg{\min_G \max_D V(D,G)} \]

结合Introduction小节的GAN训练步骤来说：

  1. 第一步：固定G的参数，用其生成的数据与真实数据混洗送入D，D通过这些数据最大化其目标函数\(V(D,G)\)
  2. 第二步：固定住D的参数，G通过不断生成数据并送入D，通过D的feedback进行最小化自己的目标函数\(\max_D V(D,G)\)

WGAN

最初GAN使用的是JS散度来衡量\(P_G\)和\(P_{data}\)之间的差异的，然而JS散度有一个致命的缺点就是，当两个概率分布之间完全没有重叠的时候JS散度是一个常数，则此时神经网络就会出现梯度消失而导致无法训练，WGAN就是通过将近似JS散度公式改写成Wasserstein距离来克服JS散度的缺点，达到了较好的效果，这里就不细讲了，论文：《Wasserstein GAN》

然而还有很多种divergence可以用在GAN中，这篇论文《f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization》就推导出在使用不同divergence时的目标函数并测试了他们。

普通GAN和Conditional GAN

图3 GAN和Conditional GAN

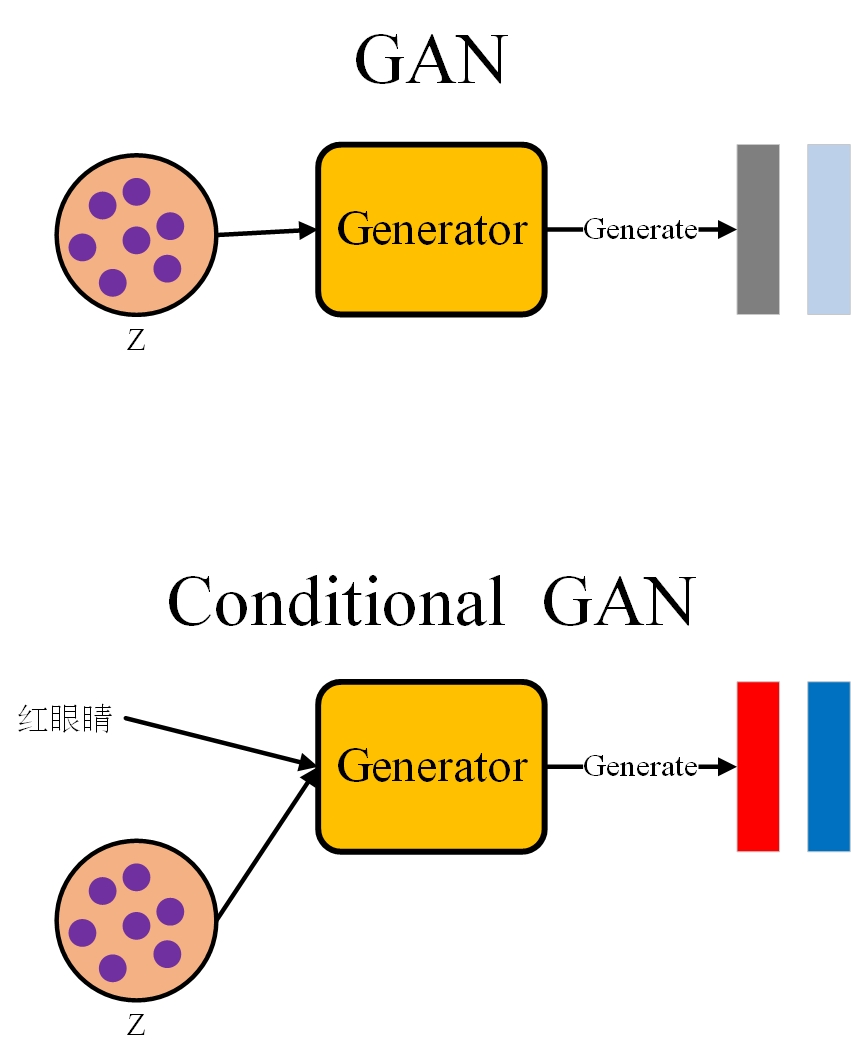
而对于输入GAN的vector，李宏毅老师讲了两种vector的获取方法（如图3）：

  1. 第一种是普通的GAN，其输入向量通常从一个简单的概率分布（例如高斯分布）中随机抽样出来并送入Generator中
  2. 第二种是Conditional GAN，其输入通常是将普通GAN的输入和一个条件vector结合后输入到Generator中

GAN的评估方法

对于生成模型，我们通常想让其生成的数据同真实数据越接近越好，并且生成的数据要保证一定的多样性，而常用的评估指标有Inception Score(IS)和FID，其实还有很多GAN的评估方法，可以参考论文：《Pros and Cons of GAN Evaluation Measures》

posted @ 2021-07-02 17:12  zhangzeff  阅读(171)  评论(0)    收藏  举报