图的边存储--链式前向星

链式前向星是在看差分约束的题的时候偶然间看到的，一开始没太重视它，感觉好像没怎么听说过。还要定义结构体，而且需要辅助数组，感觉挺麻烦的。还不如直接用STL的vector+pair定义的邻接表好用。但是后来发现大家写SPFA的时候都用的链式前向星，感觉还是写个博客学习一下吧，以前都没听说过，太菜了。。。

边存储结构存的都是有向边！！！

优缺点

优点

• 适用范围广，基本上所有图论的题都能用链式前向星来存储。
• 存储效率高，像邻接表一样不会存储不存在的边
• 可以用来替代邻接表，用vector实现邻接表好像容易爆内存(看别人说的)好像也确实，vector在容量不够时会重新开辟一个两倍于原来大小的数组。

缺点

• 邻接表的缺点它都有，
  • 无法判断重边(必须遍历查找)
  • 无法操作某个特定的边(必须遍历查找)
• 相对于邻接矩阵来说不容易实现和理解

代码实现

struct Edge
{
     int net;//1.
     int to;
     int w;
}edge[maxn];
int head[maxn], cnt=0;//2.

void add_dege(int u, int v, int w)
{
    edge[cnt].to = v;
    edge[cnt].net = head[u];//3.
    edge[cnt].w = w;
    head[u] = cnt++;
}

for(int i=head[u]; i!=-1; i=edge[i].net)//4.

注释：

1. net是next，有时候定义next可能会和系统关键字重复，所以定义为net。net指向当前边的出发结点的下一条边在edge数组中的下标。SPFA是一个bfs的过程，进行广搜时会先遍历某个顶点的所有出边，net即指向当前结点的下一条出边。to即当前边的尾结点。w即权重。
2. head[u]即存储u结点的第一个出边在edge数组中的下标。cnt即记录当前存储到edge数组的第几位了，用来设置数组下标。
3. 链式前向星是反着存储的，即先输入的边存在后面，有些类似于栈，后进先出。当a的第一条出边存入edge数组中，net等于head[u]，即-1。(所有head初始化为-1，-1表示没有边存入)之后head[u]被赋值为cnt，即刚输入的那条边在edge数组中的下标。当a的第二条边存入edge数组时，net等于head[u]，此时head[u]存的是上一次存储以u为出边的边在edge数组中的下标。每次head[u]存储的都是上一个u的边，所以遍历的时候是先遍历最后输入u的边。
4. 链式前向星遍历结点u所有出边的方法，当等于-1时表示没有下一条边了，遍历结束。

举例

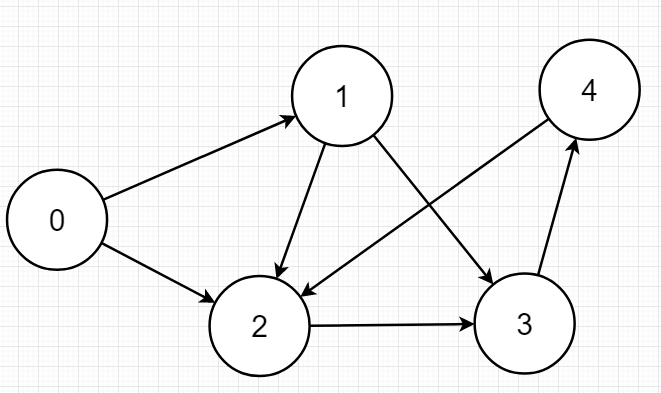
输入顺序为：

u = 0	v = 1
u = 1	v = 3
u = 0	v = 2
u = 2	v = 3
u = 1	v = 2
u = 3	v = 4
u = 4	v = 2

手动模拟一下

edge[0].to = 1	edge[0].net = -1	head[0] = 0	cnt = 0
edge[1].to = 3	edge[1].net = -1	head[1] = 0	cnt = 1
edge[2].to = 2	edge[2].net = 0	head[0] = 2	cnt = 2
edge[3].to = 3	edge[3].net = -1	head[2] = 0	cnt = 3
edge[4].to = 2	edge[4].net = 0	head[1] = 4	cnt = 4
edge[5].to = 4	edge[5].net = -1	head[3] = 5	cnt = 5
edge[6].to = 2	edge[6].net = -1	head[4] = 6	cnt = 6

上图中0的出边有两条，在edge数组中的存储位置分别为0、2，最后head[0] = 2；当遍历以0为起点的边时，先从edge[2]开始遍历，可发现edge[2].net = 0;即以0为起点的最后一条边。可看出，遍历和输入顺序是相反的，但是并不影响结果。

参考

1. [不知道为什么404了](https://blog.csdn.net/acdreamers/article/details/16902023()
2. ACM图论之存图方式