洛谷 P6965 [NEERC 2016] Binary Code /「雅礼集训 2017 Day4」编码 【经验值记录】（2-SAT 学习笔记）

其实是一篇薛定谔的题解（因为贺了inf篇题解）
玩了我一下午的题(感觉至少是一个上位紫🟣）
啊啊啊啊啊好恶心啊使我san值狂掉！
感觉自己做的话一周也写不出来

前置知识

2-SAT(拓扑排序,trajan求强连通分量),前后缀优化建图,01trie树（数据结构优化建图)
好好好。
让我们一个一个的搞定它们

2-SAT

定义：

2-SAT就是2-SAT
其实直接OIWIKI
image

image
2-SAT问题例子：
假设CSP-S后教练要请HZOI吃饭，但不知道吃啥，于是让所有人提出两个要求，每个人至少被满足一个要求

js:1.我不吃米酒蛋花汤 2.我要吃虾仁饭
gyh:1.我要吃米酒蛋花汤 2.我不吃红烧鱼
css:1.我要吃牛蛙（gyh） 2.我不吃虾仁饭
zzx:1.我要吃火锅 2.我不吃牛蛙（gyh）
lzk:1.我不吃牛蛙(gyh) 2.我要（吃）堂吉诃德
wyx:1.我不喝手调黑暗饮料 2..我要吃lc买的烧鸡
skk:1.我要喝手调黑暗饮料 2.我不吃lc买的烧鸡
……………………

所以合法的一个菜单是:
火锅，堂吉诃德，手调黑暗饮料，lc买的烧鸡？？(css提供）

解法

有两种十分明显且时间复杂度很劣的解法：二进制枚举、深度优先搜索。（因为压根没用所以此处不再列举）
直接跳到最优的解法

tarjan

我们可以将给出的条件转化成为一张有向图:

即将问题转化成 若第 \(i\) 个元素为 \(a\) ，则第 \(j\) 个元素必定为 \(b\) 这种形式。

我们可以发现这种限制条件带有指向性，就像一条有向边。

于是我们定义一条有向边 \((u−>v)\) 为若 \(u\) 成立则 \(v\) 一定成立。

但2-SAT问题的一个元素有两种状态，该元素被满足（1），该元素不被满足（0）。（即上文的css要吃牛蛙，但zzx不要吃牛蛙）

发现用一个点是不好表示的，考虑拆点。

一般用标号为\(i\)这个点来表示\(i\)这个元素为\(0\)（不吃牛蛙），用标号为\(i+n\)这个点来表示\(i\)这个元素为\(1\)。（吃牛蛙）

显然，若可以通过建好的有向图从将\(i\)拆点后得到的两个点\(i\)跑到\(i+n\)，该\(i\)元素成立一定是不合法的，\(i+n\)暂时是合法的。反之，若能从\(i+n\)跑到\(i\)，该\(i+n\)元素成立一定是不合法的，\(i\)暂时是合法的。

以下将对一个元素拆点后得到的两个点叫做\(u,v\)。

如何确定一条有向图上的路径 \((u−>v)\) 呢？

先假设我们建出来的图是一个有向无环图（\(DAG\)），那么进行拓扑排序之后，一旦存在一条 \((u−>v)\) 的路径，那么 \(u\) 的拓扑序一定小于 \(v\) 的拓扑序，也就是说一个元素拆点后合法的点的拓扑序一定大于非法点。

但问题来了，建成的图不一定是一个\(DAG\)，如何处理环的情况呢？

这时就可以使用\(tarjan\)的强连通分量算法将一个带环的图强制转化成一个\(DAG\)。

以下给出强连通分量的性质

强连通分量的性质：一个强连通分量里的任意两个点可以互相到达，即任意两个点之间都有以一条以对方为起点自己为终点和自己为起点对方为终点的路径。

求出强连通分量之后不需要缩点再跑拓扑排序，只需进行强连通分量的标号大小比较就行。分量标号较小的那个即为合法点。

考虑原因：

思考强连通算法的实现过程，如果跑完Tarjan缩点之后呈现出的拓扑序更大（合法点），在Tarjan会更晚被遍历到，就会更早地被弹出栈（先进后出）而缩点，分量编号会更小。所以 Tarjan 求得的强连通分量编号相当于 反拓扑序。

让我们回到那个暂时

\(i+n\)暂时是合法的

为什么呢?
若\(i+n\)也有一条合法的路径走到\(i\),那么他们的两种决策都不合法，那用强连通分量如何判断呢？

让我们回顾Tarjan强连通分量的定义，发现若两个点可以互相到达，那么它们一定属于同一个强连通分量，所以对一个拆点得到的两个点\(i\)和\(i+n\)来说，若他们的强连通分量标号是相同的，那么整个问题无解。

那如果\(i\)和\(i+n\)没有一条合法的路径使他们联通，即\(i\)走不到\(i+n\)且\(i+n\)也走不到\(i\)。那又应该如何记录答案呢？

我们发现，无论该元素状态是\(0\)还是\(1\),都是合法的，所以选择强连通分量标号较小的那个就可以了。

tips:2-SAT 的建边要将所有能肯定的情况全部建出来。
以下列出常见情况的建边方式：

设 \(a\) 表示 \(x_a\) 为真（要吃牛蛙）（\(\neg a\) 就表示 \(x_a\) 为假（不吃牛蛙）），\(𝑎 ∨𝑏\)表示变量\(a,b\)至少满足一个
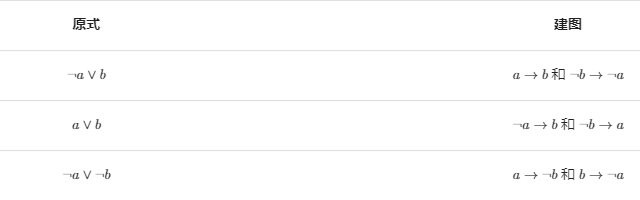
image

那对应上文，HZOI 的要求图为：

吃米酒蛋花汤->吃虾仁饭
不吃虾仁饭->不吃米酒蛋花汤
吃红烧鱼->吃米酒蛋花汤
不吃米酒蛋花汤->不吃红烧鱼
吃虾仁饭->吃牛蛙
不吃牛蛙->不吃虾仁饭
不吃火锅->不吃牛蛙
吃牛蛙->吃火锅
不吃堂吉诃德->不吃牛蛙
吃牛蛙->吃堂吉诃德
不喝手调暗黑饮料->不吃lc买的烧鸡
吃lc买的烧鸡->喝手调暗黑饮料
不喝手调暗黑饮料->不吃lc买的烧鸡（重边）
吃lc买的烧鸡->喝手调暗黑饮料（重边）

让我们做一个例题

例题

洛谷 P4782 【模板】2-SAT

image

直接按上面贺的OIwiki的图建遍即可，主要看代码实现：

代码

#include<bits/stdc++.h>
using namespace std;
int h[2000010],to[2000010],nxt[2000010],tot;//链式前向星
int dfn[2000010],low[2000010],scc[2000010];//时间戳，追溯值，强连通分量标号 
int cntdfn,cntscc;//dfs序，强连通分量个数 
bool vis[2000010]; 
stack <int> s;//tj所需的栈（手写也行但我懒 
void add(int x,int y)//链式前向星建边 
{
    tot++;
    to[tot]=y;
    nxt[tot]=h[x];
    h[x]=tot;
}
void tarjan(int x)//tj求强连通分量 
{
	cntdfn++;
	dfn[x]=cntdfn;
	low[x]=cntdfn;
	s.push(x);
	vis[x]=1;
	for(int i=h[x];i;i=nxt[i])
	{
		int y=to[i];
		if(!dfn[y])
		{
		    tarjan(y);
	        low[x]=min(low[x],low[y]);
		} 
		else if(vis[y])
		{
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(dfn[x]==low[x])
	{
		cntscc++;
		int y;
		do
		{
			y=s.top();
			s.pop();
			vis[y]=0;
			scc[y]=cntscc;
		}while(x!=y);
	}
}
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x,a,y,b;
		cin>>x>>a>>y>>b; 
		add(y+n*(b^1),x+n*(a&1));//建边，此处使用位运算简化（也可以将情况分类 
		add(x+n*(a^1),y+n*(b&1));
	}
	for(int i=1;i<=2*n;i++)//拆点 
	{
		if(!dfn[i])//求强连通分量 
		{
			tarjan(i);
		}
	}
	for(int i=1;i<=n;i++)
	{
	    if(scc[i]==scc[i+n])//若拆下来的两个点标号相同，则此题无解 
		{
		    cout<<"IMPOSSIBLE";
		    return 0;
		}	
	} 
	cout<<"POSSIBLE"<<endl;
	for(int i=1;i<=n;i++)
	{
	    if(scc[i]<scc[i+n])//输出方案，scc标号较小的为合法点(即拓扑序较大 
		{
		    cout<<0<<" ";
		}	
		else
		{
			cout<<1<<" ";
		}
	} 
	return 0;
}

如果你tarjan板子忘了的话link
因为来自毛竹259，所以……

前后缀优化建图

这是啥？

就是使用前后缀的方式优化建图

举个栗子（例题）：

假设HZOI有100219个人，分为了28个帮派（大雾！），每个帮派要选出来一个头头出来开会，但又有一些神秘二人关系，使得他们两个至少有一个人出现在帮派大会，否则会丢失一些【数据删除】，问这帮派大会是否可以举办?

eeeeee这例子太抽象了
给一个形式化题意

洛谷 P6378 [PA 2010] Riddle

image

如何转换成我们刚学的问题（2-SAT）呢？

考虑将头发染成绿的（bushi）将每一个参加大会（头头）染成黑的（则不参加的是白的），发现了如下的关系：

  • 若\(gyh\)是黑的，则她所处的帮派其余人是白的
  • 若\(gyh\)是白的，则她的npy二人关系中的另一个人是黑的
  • 其实\(gyh\)是绿的

然后你就可以愉快地建边啦嘻嘻嘻嘻嘻嘻

但你不愉快的发现：

image

炸炸炸，如果\(gyh\)在一个大帮派里或者是海王（有好几个npy二人关系)，那你将获得几个黑黑的\(TLE\)（她太坏惹！谴责她！！）

那怎么办啊?

发现你建的边是有传递性的，现在就可以使用前后缀优化建图啦！

前后缀优化建图包括前缀和后缀,该题的前缀定义为其所属部分出现在当前输入的所有点（即\(x\)的前缀是在\(x\)的帮派中比它先输入的所有人），后缀定义为其所属部分没有出现在当前输入的所有点（即\(x\)的后缀是在\(x\)的帮派中比它后输入的所有人）考虑创建一些虚点来表示该点的前缀或后缀有黑点。

则对于\(x\)这个元素，其有四个点与它有关：

  • \(x_1\):该元素是白点（用\(x\)表示）
  • \(x_2\):该元素是黑点（用\(x+n\)表示）
  • \(x_3\):该元素的后缀中有一个黑点（用\(x+2*n\)）
  • \(x_4\):该元素的前缀中有一个黑点（用\(x+3*n\)）

然后可以进行一个连边的操作了:

通过一些逻辑推理可得：

对于一些二人关系(\(x\),\(y\))：

\(x_1->y_2\)
\(x_2->y_1\)

对于一些帮派关系（即\(y\)是\(x\)的向前的一个点):

\(x_3->x_1\)
\(x_4->x_1\)
\(x_2->y_3\)
\(y_2->x_4\)
\(x_3->y_3\)
\(y_4->x_4\)

剩下的就是一个\(2-SAT\)板子啦嘻嘻嘻嘻嘻

代码实现

#include<bits/stdc++.h>
using namespace std;
int h[4000010],nxt[8000010],to[8000010],tot;
stack <int> s;
bool vis[4000010];
int dfn[4000010],low[4000010],scc[4000010],cntscc,cntdfn;
void add(int x,int y)
{
	tot++;
	to[tot]=y;
	nxt[tot]=h[x];
    h[x]=tot;	
}
void tarjan(int x)
{
	cntdfn++;
	dfn[x]=cntdfn;
	low[x]=cntdfn;
	s.push(x);
	vis[x]=1;
	for(int i=h[x];i;i=nxt[i])
	{
		int y=to[i];
		if(!dfn[y])
		{
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(vis[y])
		{
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(dfn[x]==low[x])
	{
		cntscc++;
		int y=-1;
		do
		{
		    y=s.top();
			s.pop();
			vis[y]=0;
			scc[y]=cntscc;	
		}while(x!=y);
	}
}
int main()
{
	int n,m,k;
	cin>>n>>m>>k;
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		add(x,y+n);
		add(y,x+n); 
	}
	for(int i=1;i<=k;i++)
	{
		int w;
		cin>>w;
		int y=0;
		for(int j=1;j<=w;j++)
		{
			int x;
			cin>>x;
			add(x+2*n,x);
			add(x+3*n,x);
			if(y)
			{
				add(x+n,y+2*n);
				add(y+n,x+3*n);
				add(x+2*n,y+2*n);
				add(y+3*n,x+3*n);
			}
			y=x;
		}
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])
		{
		    tarjan(i);	
		} 
	}
	for(int i=1;i<=n;i++)
	{
        if(scc[i]==scc[i+n])
        {
        	cout<<"NIE";
        	return 0;
		}
	}
	cout<<"TAK"; 
	return 0;
}

等等等我还没写完，先存一下

posted @ 2025-10-27 21:53  BIxuan—玉寻  阅读(45)  评论(12)    收藏  举报