图论模板

目录

• 树基础
  • 知道先序遍历和中序遍历，输出后序遍历
  • 普通树转二叉树&二叉树的前序、中序、后序遍历
  • BFS
  • DFS（邻接矩阵）
  • DFS（邻接链表）
  • DFS（vector存边）
• dfs序
• 欧拉序
  • 欧拉序1
  • 欧拉序2
• 欧拉路&欧拉回路
• 最短路
  • Floyed
  • Dijkstra
    • 朴素的Dijkstra & 邻接矩阵存图
    • 朴素的Dijkstra & 链式前向星存图
    • 堆优化Dijkstra & 链式前向星存图
  • Bellman-Ford算法
  • spfa算法
  • 判断负环
    • bfs写法
    • dfs写法
  • 二维最短路
• 最小生成树
  • 朴素版prim算法
  • 堆优化prim算法
  • Kruskal
• 拓扑排序
• 二分图
• 差分约束
  • 判断是否合法
  • 求最小值
• 最近公共祖先（LCA）
  • 倍增法
  • tarjan算法求lca
• 树链剖分
  • 例题
• Tarjan
  • 一些概念
  • 割边
    • 割边算法模板
  • 割点
    • 割点算法模板
  • 无向图的双连通分量
    • 边双连通分量（e-DCC）的求法模板：
    • e-DCC的缩点模板：
    • 点双连通分量（v-DCC）的求法模板：
    • v-DCC的缩点模板：
  • 有向图连通性
    • scc算法模板：
    • scc缩点模板：
• 树链剖分
  • 重链剖分
    • 概念
    • 一些定义
    • 一些性质
    • 应用
    • 具体实现
    • 例题

树基础

知道先序遍历和中序遍历，输出后序遍历

//s1先序遍历，s2中序遍历，输出后序遍历
void work(string s1, string s2)
{
	int len = s1.size();
	if(len == 1) 
	{
		cout << s1[0];
		return;	
	}	
	
	//求根在中序遍历中的位置
	int k = s2.find(s1[0]);
	
	string s3, s4;
	if(k > 0)	//如果位置大于0，表明有左子树
	{
		s3 = s1.substr(1, k);	//左子树的前序遍历
		s4 = s2.substr(0, k);	//左子树的中序遍历
		work(s3, s4);
	}
	if(k < len - 1)	//如果位置小于最后一个字符的下标表明有右子树
	{
		s3 = s1.substr(k+1, len-k-1);	//右子树的前序遍历
		s4 = s2.substr(k+1, len-k-1);	//右子树的中序遍历
		work(s3, s4);
	}
	cout << s1[0];
}

普通树转二叉树&二叉树的前序、中序、后序遍历

题目：提高组题库【133】普通树转二叉树

#include <bits/stdc++.h>
using namespace std;

const int maxn = 30;
struct node
{
	char data;
	int lson, rson;
}tr[maxn] = {};
int n = 0;

//前序遍历
void preorder(int rt)
{
	printf("%c", tr[rt].data);
	if(tr[rt].lson) preorder(tr[rt].lson);
	if(tr[rt].rson) preorder(tr[rt].rson);
}

//中序遍历
void inorder(int rt)
{ 
	if(tr[rt].lson) inorder(tr[rt].lson);
	printf("%c", tr[rt].data);
	if(tr[rt].rson) inorder(tr[rt].rson);	
}

//后序遍历
void postorder(int rt)
{
	if(tr[rt].lson) postorder(tr[rt].lson);
	if(tr[rt].rson) postorder(tr[rt].rson);	
	printf("%c", tr[rt].data);	
}

int main()
{
	int x = 0, y = 0;
	//
	//要将普通树转为二叉树
	scanf("%d", &n);
	for(int i=1; i<=n; i++)
	{
		scanf(" %c", &tr[i].data);
		//
		//第一个叶子节点作为左子树
		scanf("%d", &x);
		if(x == 0) continue;
		tr[i].lson = x;
		//
		//剩下的叶子节点依次链接为右链
		y = x;
		while(1)
		{
			scanf("%d", &x);
			if(x == 0) break;
			tr[y].rson = x;
			y = x;
		}
	}
	
	//输出前序遍历
	preorder(1);
	printf("\n");
	//输出后序遍历
	postorder(1);
	
	return 0;
}

BFS

#include <bits/stdc++.h>
using namespace std;

const int maxn = 10010;

int n = 0, m = 0;
bool g[maxn][maxn] = {};
queue<int> q;
bool vis[maxn] = {};

void bfs(int x)
{
	q.push(x);
	vis[x] = true;
	
	while(!q.empty())
	{
		int t = q.front();
		printf("%d ", t);
		q.pop();
		
		for(int i=1; i<=n; i++)
		{
			if(g[t][i] && !vis[i])
			{
				q.push(i);
				vis[i] = true;
			}
		}
	}
}

int main()
{	
	int x = 0, y = 0;
	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		g[x][y] = g[y][x] = 1;
	}
	
	bfs(1);
	
	return 0;
}

DFS（邻接矩阵）

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110;

int n = 0, m = 0;
int g[maxn][maxn] = {};
bool vis[maxn] = {};

void dfs(int x)
{
	vis[x] = true;
	printf("%d ", x);
	
	for(int i=1; i<=n; i++)
	{
		if(!vis[i] && g[x][i])
		{
			dfs(i);
		}
	}
}

int main()
{
	int x = 0, y = 0;
	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		g[x][y] = g[y][x] = 1;
	}

	dfs(1);

	return 0;
}

DFS（邻接链表）

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110;
const int maxm = 10010;

int n = 0, m = 0;
int h[maxn] = {}, tot = 0;
struct edge
{
	int to, nxt;
}e[maxm];
int v[maxn] = {};

void addedge(int x, int y)
{
	++tot;
	e[tot].to = y;
	e[tot].nxt = h[x];
	h[x] = tot;
}

void dfs(int x)
{ 
	printf("%d ", x);
	v[x] = true;
	
	for(int i=h[x]; i; i=e[i].nxt)
	{
		int y = e[i].to;
		if(!v[y])
		{ 
			dfs(y); 
		}
	}
}

int main()
{	
	int x = 0, y = 0;
	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}
	
	dfs(1);
	
	return 0;
}

DFS（vector存边）

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110; 

int n = 0, m = 0;
vector<int> e[maxn];
bool v[maxn] = {};

void dfs(int x)
{
	v[x] = true;
	printf("%d ", x);
	
	for(auto y : e[x])
	{
		if(!v[y])
		{
			dfs(y);
		}
	}
}

int main()
{	
	int x = 0, y = 0;
	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		e[x].push_back(y);
		e[y].push_back(x);
	}
	
	dfs(1);
	
	return 0;
}

dfs序

dfs序不是唯一的
dfs序一般用于树状结构中，如图：

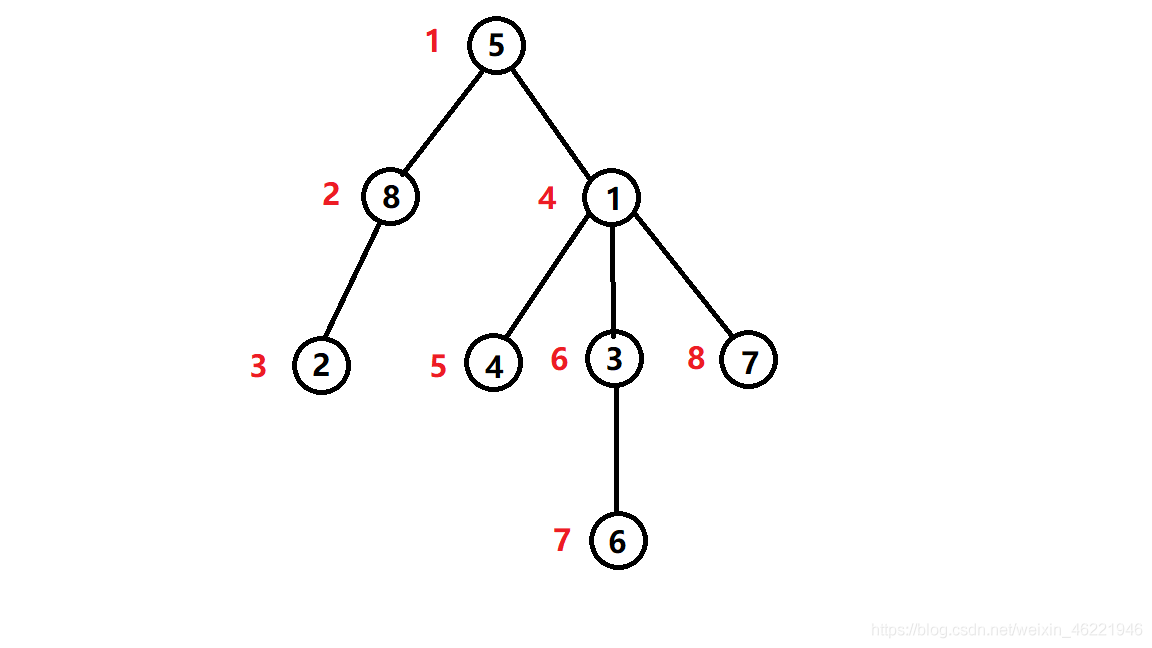
图中红色序号为每个点对应的dfs序序号，黑色序号为每个点默认的序号，我称之为节点序序号（下文同）
可见，dfs序如其名，dfs序序号是按照dfs顺序标记的，所以说给每个节点安排上dfs序序号也很简单，只要dfs的时候顺便标上就行了，dfs第多少次就给dfs到的点标为多少。

void dfs(int x)
{
	vis[x] = true;
	a[++cnt] = b[x];	//a数组记录的就是dfs序
	in[x] = cnt;	//记录以x为根节点的子树，在dfs序中开始的下标

	int v = 0;	
	for(int i=head[x]; i; i=nxt[i])
	{
		v = to[i];
		if(vis[v]) continue;
		
		dfs(v);
	}
	out[x] = cnt;//记录以x为根节点的子树，在dfs序中结束的下标
}

dfs序的主要作用就是将一个子树变成序列上的一个连续区间。
还是以上图为例，

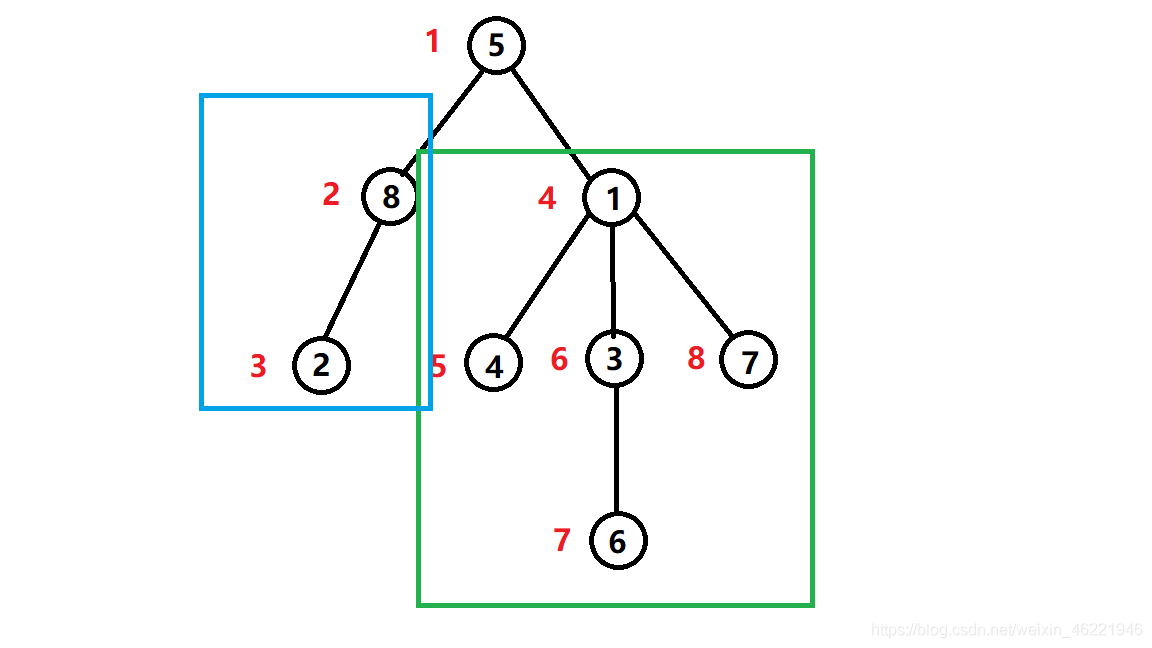
绿色子树可以通过dfs序序号表示出来，4~8；
红色子树表示为2~3；
显然，可以用一连续区间表示出来任意子树。
这样的变换可以解决类似“修改树上某点，输出子树和或者最大值最小值”等问题。
常常配合线段树或树状数组。

欧拉序

欧拉序长得跟dfs序相差无几
储存的则是从根节点开始，按照dfs的顺序经过所有点再绕回原点的路径
共存在两种欧拉序

欧拉序1

这一种欧拉序相当于是在dfs的时候，如果储存节点的栈变化一次，就把栈顶的节点编号记录下来,也就是说，每当访问完一个节点的子树，则需要返回一次该节点，再继续搜索该节点的其余子树,在树上的移动过程为

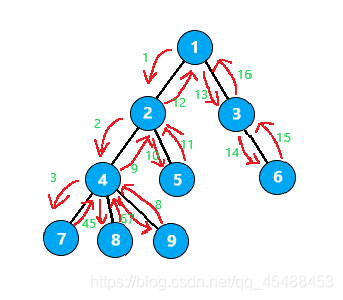
它的搜索顺序便是
1 2 4 7 4 8 4 9 4 2 5 2 1 3 6 3 1
搜索代码：

void euler_dfs1(int p)
{
    euler_order1[++pos]=p;
    vis[p]=true;
    for(int i:G[p])
        if(!vis[i])
        {
            euler_dfs1(i);
            euler_order1[++pos]=p; //与dfs序的差别，在搜索完一棵子树后就折返一次自己
        }
} //数组需要开2倍n大

欧拉序2

这一种欧拉序相当于是在dfs的时候，如果某个节点入栈，就把这个节点记录下来，直到后面的操作中这个节点出栈，再记录一次这个节点
也就是说，每个节点严格会在记录中出现两次，第一次是搜索到它的时候，第二次是它的子树完全被搜索完的时候
除根节点外，每个节点严格两个入度两个出度
在树上的移动过程为

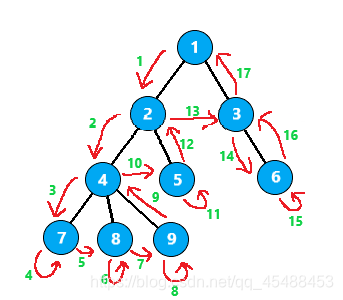
它的搜索顺序便是
1 2 4 7 7 8 8 9 9 4 5 5 2 3 6 6 3 1
可以发现，某个节点在顺序中出现的两次所围成的区间，就表示这个节点与它的子树
欧拉序 2 的搜索代码：

void euler_dfs2(int p)
{
    euler_order2[++pos]=p;
    vis[p]=true;
    for(int i:G[p])
        if(!vis[i])
            euler_dfs2(i);
    euler_order2[++pos]=p; //与dfs序的差别，在所有子树搜索完后再折返自己
} //数组需要开2倍n大

欧拉路&欧拉回路

如果一个图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。

我们定义奇点是指跟这个点相连的边数目有奇数个的点。对于能够一笔画的图，我们有以下两个定理。
定理1：存在欧拉路的充要条件：图是连通的，有且只有2个奇点。
定理2：存在欧拉回路的充要条件：图是连通的，有0个奇点。

两个定理的正确性是显而易见的，既然每条边都要经过一次，那么对于欧拉路，除了起点和终点外，每个点如果进入了一次，显然一定要出去一次，显然是偶点。对于欧拉回路，每个点进入和出去次数一定都是相等的，显然没有奇点。

求欧拉路的算法：寻找节点的度为奇数的点，作为欧拉路的起点，执行深度优先遍历即可。
求欧拉回路的算法：以任意一个点为起点，执行深度优先遍历即可
例题：提高组题库，骑马修栅栏

#include <bits/stdc++.h>
using namespace std;

const int maxn = 510; 

int n = 0, m = 0; //n表示点数
int g[maxn][maxn] = {}; 
int du[maxn] = {};

void dfs(int x)
{
	printf("%d\n", x);
	
	//保证先搜顶点号小的，再搜顶点号大的
	for(int i=1; i<=n; i++)
	{
		if(g[x][i]) 
		{
			g[x][i]--;
			g[i][x]--;
			dfs(i);	
		}
	}
}

int main()
{
	int x = 0, y = 0;
	scanf("%d", &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		g[x][y]++;
		g[y][x]++;
		du[x]++;
		du[y]++;
		if(n < x) n = x;
		if(n < y) n = y;
	}
	
	//寻找节点的度为奇数的点，作为欧拉路的起点
	//没有度为奇数的点，则从1开始，求欧拉回路
	int st = 1;
	for(int i=1; i<=n; i++)
	{
		if(du[i] % 2 == 1)
		{
			st = i;
			break;
		}
	}
	
	dfs(st);
	
	return 0;
}

最短路

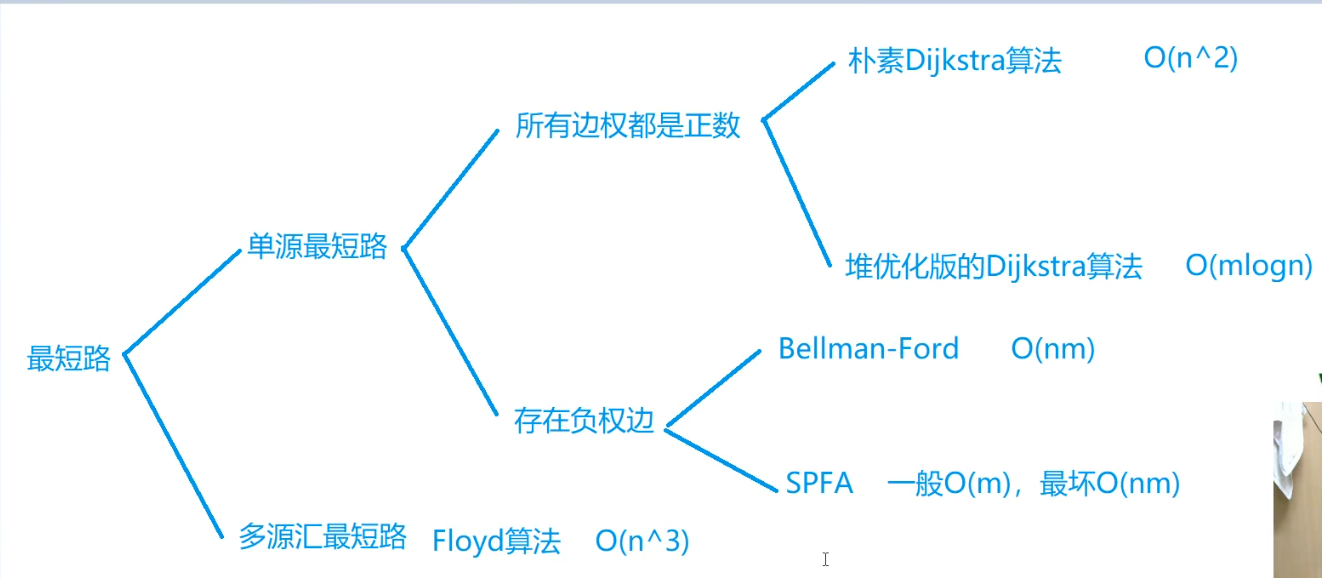
Floyed

时间复杂度是\(O(n^3)\),n表示点数。

//初始化
memset(dis, 0x3f, sizeof(dis));
for(int i=1; i<=n; i++) dis[i][i] = 0;

//算法结束后，dis[x][y]表示x到y的最短距离
void floyd()
{
	for(int k=1; i<=n; k++)
	{
		for(int i=1; i<=n; i++)
		{
			for(int j=1; j<=n; j++)
			{
				dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
			}
		}
	}
}

Dijkstra

朴素的Dijkstra & 邻接矩阵存图

时间复杂度是\(O(n^2+m)\),n表示点数,m表示边数
例题：提高组题库，148信使

//初始化
#include <bits/stdc++.h>
using namespace std;

const int maxn = 510;
const int inf = 0x7f7f7f7f;

int n = 0, m = 0;
int g[maxn][maxn] = {};	//朴素版的dijkstra算法多用与稠密图，因此用邻接矩阵存图
int dis[maxn] = {};	//存储1号点到每个点的最短距离
int vis[maxn] = {}; //存储每个点的最短路是否已经确定

void dij()
{
	memset(dis, 0x3f, sizeof(dis));
	dis[1] = 0;
	
	for(int i=1; i<n; i++)
	{
		int t = -1;
		//在还未确定最短路的点中，寻找距离最小的点
		for(int j=1; j<=n; j++)
		{
			if(!vis[j] && (t==-1 || dis[t]>dis[j])) t = j;
		}
		
		//用t更新其他点的距离
		for(int j=1; j<=n; j++)
		{
			dis[j] = min(dis[j], dis[t] + g[t][j]);
		}
		vis[t] = true;
	}
}

int main()
{	
	int x = 0, y = 0, z = 0;
	
	scanf("%d%d", &n, &m);
	memset(g, 0x3f, sizeof(g));
	for(int i=1; i<=n; i++) g[i][i] = 0;
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &x, &y, &z);
		g[x][y] = g[y][x] = z;
	}
	
	dij();
	
	int ans = 0;
	for(int i=1; i<=n; i++)
	{
		if(dis[i] == 0x3f3f3f3f) 
		{
			printf("-1");
			return 0;
		}
		if(ans < dis[i]) ans = dis[i];
	}
	printf("%d", ans);
    
	return 0;
}

朴素的Dijkstra & 链式前向星存图

例题：提高组题库，148信使

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110;
const int maxm = 10010;
 
int n = 0, m = 0;
int h[maxn] = {}, to[maxm] ={}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
int dis[maxn] = {}, vis[maxn] = {};

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	w[tot] = z;
	nxt[tot] = h[x];
	h[x] = tot;
}

void dij()
{
	memset(dis, 0x3f, sizeof(dis));
	dis[1] = 0;
	
	for(int i=1; i<=n; i++)
	{
		int t = -1;
		for(int j=1; j<=n; j++)
		{
			if(!vis[j] && (t == -1 || dis[t] > dis[j])) t = j;
		}
		
		for(int i=h[t]; i; i=nxt[i])
		{
			int y = to[i];
			dis[y] = min(dis[y], dis[t] + w[i]);
		}
		vis[t] = true;
	}
}

int main()
{     
	int x = 0, y = 0, z = 0;
	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &x, &y, &z);
		addedge(x, y, z);
		addedge(y, x, z);
	}
	
	dij();
	
	int ans = 0;
	for(int i=1; i<=n; i++)
	{
		ans = max(ans, dis[i]);
	}
	if(ans == 0x3f3f3f3f) printf("-1\n");
	else printf("%d\n", ans);
 
	return 0;
} 

堆优化Dijkstra & 链式前向星存图

时间复杂度是\(O(mlog(n))\),n表示点数,m表示边数
例题：提高组题库，148信使

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110;
const int maxm = maxn * maxn;
const int inf = 0x7f7f7f7f;

int n = 0, m = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
int dis[maxn] = {}; 
bool vis[maxn] = {}; 
priority_queue<pair<int, int>> q;

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	w[tot] = z;
	h[x] = tot;
}

void dij(int x)
{
	memset(dis, 0x3f, sizeof(dis));
	dis[x] = 0;
	q.push(make_pair(0, x));
	 
	while(q.size())
	{ 
		x = q.top().second;
		q.pop();
		if(vis[x]) continue;
		vis[x] = true;
		
		for(int i=h[x]; i; i=nxt[i])
		{
			int y = to[i];
			if(dis[y] > dis[x] + w[i])
			{
				dis[y] = dis[x] + w[i];
				q.push(make_pair(-dis[y], y));
			}
		}
	}
}
 
int main()
{	
	int x = 0, y = 0, z = 0;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &x, &y, &z);
		addedge(x, y, z);
		addedge(y, x, z);
	}
	
	dij(1);
	
	int ans = 0;
	for(int i=1; i<=n; i++)
	{
		if(dis[i] == 0x3f3f3f3f) 
		{
			printf("-1");
			return 0;
		}
		if(ans < dis[i]) ans = dis[i];
	}
	printf("%d", ans);

	return 0;
}

Bellman-Ford算法

在最短路存在的情况下，由于一次松弛操作会使最短路的边数至少+1，而最短路的边数最多为n-1,
因此整个算法最多执行n-1轮松弛操作。
故时间复杂度为O(nm)

判断负环：
如果图中有负环，松弛操作会无休止的进行下去。
因此，我们循环n次，n轮循环时，仍然存在能松弛的边，说明存在负环

时间复杂度是\(O(nm)\),n表示点数,m表示边数
可以用该算法求最长路
例题：提高组题库，148信使

#include <bits/stdc++.h>
using namespace std;

/*
在最短路存在的情况下，由于一次松弛操作会使最短路的边数至少+1，而最短路的边数最多为n-1,
因此整个算法最多执行n-1轮松弛操作。
故时间复杂度为O(nm)

判断负环：
如果图中有负环，松弛操作会无休止的进行下去。
因此，我们循环n次，n轮循环时，仍然存在能松弛的边，说明存在负环
*/

const int maxn = 110;
const int maxm = maxn * maxn; 
const int inf = 0x3f3f3f3f;

int n = 0, m = 0;
int dis[maxn] = {};
struct edge
{
	int x, y, w;
}e[maxm];

bool bellman_ford()
{
	memset(dis, 0x3f, sizeof(dis));
	dis[1] = 0;
	
	bool flag = false;	//判断一轮循环过程中是否发生松弛操作
	for(int i=1; i<=n; i++)
	{
		flag = false;
		for(int j=1; j<=m*2; j++)
		{
			int x = e[j].x, y = e[j].y, w = e[j].w;
			//无穷大与常数加减仍然为无穷大
			//因此最短路长度为inf的点引出的边不可能发生松弛操作
			if(dis[x] == inf) continue;
			if(dis[y] > dis[x] + w)
			{
				dis[y] = dis[x] + w;
				flag = true;
			}
		}
		//没有可以松弛的边时就停止算法
		if(!flag) break;
	}
	//第n轮循环仍然可以松弛时说明存在负环
	return flag;
}
 
int main()
{	
	int x = 0, y = 0, z = 0;

	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &x, &y, &z);
		//无向图，边需要加两次
		e[i].x = x;
		e[i].y = y;
		e[i].w = z;
		e[m+i].x = y;
		e[m+i].y = x;
		e[m+i].w = z;
	}
	
	bellman_ford();
	
	int ans = 0;
	for(int i=1; i<=n; i++)
	{ 
		if(dis[i] == 0x3f3f3f3f) 
		{
			printf("-1");
			return 0;
		}
		if(ans < dis[i]) ans = dis[i];
	}
	printf("%d", ans);

	return 0;
}

spfa算法

也叫做 队列优化的Bellman-Ford算法
时间复杂度：平均情况下是\(O(m)\),最坏情况下\(O(nm)\),n表示点数,m表示边数
例题：提高组题库，148信使

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110;
const int maxm = maxn * maxn;
const int inf = 0x7f7f7f7f;

int n = 0, m = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
int dis[maxn] = {}; 
bool vis[maxn] = {}; 
queue<int> q;

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	w[tot] = z;
	h[x] = tot;
}

void spfa(int x)
{
	memset(dis, 0x3f, sizeof(dis));
	dis[x] = 0;
	q.push(x);
	 
	while(q.size())
	{ 
		x = q.front();
		q.pop();
		vis[x] = false;
		
		for(int i=h[x]; i; i=nxt[i])
		{
			int y = to[i];
			if(dis[y] > dis[x] + w[i])
			{
				dis[y] = dis[x] + w[i];
				if(!vis[y]) q.push(y);
			}
		}
	}
}
 
int main()
{	
	int x = 0, y = 0, z = 0;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &x, &y, &z);
		addedge(x, y, z);
		addedge(y, x, z);
	}
	
	spfa(1);
	
	int ans = 0;
	for(int i=1; i<=n; i++)
	{
		if(dis[i] == 0x3f3f3f3f) 
		{
			printf("-1");
			return 0;
		}
		if(ans < dis[i]) ans = dis[i];
	}
	printf("%d", ans);

	return 0;
}

判断负环

bfs写法

使用spfa算法判断负环，有两种方法
方法 1：统计每个点入队的次数，如果某个点入队大于等于n次，则说明存在负环
方法 2：统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在负环
例题：提高题库 158.Wormholes 虫洞

判断点入队次数（方法1）
#include <bits/stdc++.h>
using namespace std;

const int maxn = 510; 
const int maxm = 6000;
const int inf = 0x3f3f3f3f;

int n = 0, m = 0, s = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
int dis[maxn] = {};
bool vis[maxn] = {};
//记录某个节点入队次数
int cnt[maxn] = {};

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	w[tot] = z;
	h[x] = tot;
}

bool spfa()
{ 
	memset(vis, 0, sizeof(vis));
	
	queue<int> q;
	for(int i=1; i<=n; i++)
	{
		q.push(i);
		vis[i] = true;		
	}

	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = false;
		
		for(int i=h[x]; i; i=nxt[i])
		{
			int y = to[i];
			if(dis[y] > dis[x] + w[i])
			{
				dis[y] = dis[x] + w[i];
				 
				if(!vis[y])
				{
					q.push(y);
					vis[y] = true;
					
					//如果某个节点入队次数>=n次，表示有负环
					cnt[y]++;
					if(cnt[y] >= n) return true;
				}
			}
		}
	}
	return false;
}

int main()
{	
	int T = 0;
	scanf("%d", &T);
	while(T--)
	{
		tot = 0;
		memset(h, 0, sizeof(h));
		memset(to, 0, sizeof(to));
		memset(nxt, 0, sizeof(nxt));
		memset(w, 0, sizeof(w));
		memset(cnt, 0, sizeof(cnt));
		
		int x = 0, y = 0, z = 0;
		scanf("%d%d%d", &n, &m, &s);
		for(int i=1; i<=m; i++)
		{
			scanf("%d%d%d", &x, &y, &z);
			addedge(x, y, z);
			addedge(y, x, z);
		}
		for(int i=1; i<=s; i++)
		{
			scanf("%d%d%d", &x, &y, &z);
			addedge(x, y, -z);
		}
		
		if(spfa()) printf("YES\n");
		else printf("NO\n");
	}

	return 0;
}

判断边数（方法2）
#include <bits/stdc++.h>
using namespace std;

const int maxn = 510; 
const int maxm = 6000;
const int inf = 0x3f3f3f3f;

int n = 0, m = 0, s = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
int dis[maxn] = {};
bool vis[maxn] = {};
//记录某条路径上边的数量
int cnt[maxn] = {};

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	w[tot] = z;
	h[x] = tot;
}

bool spfa()
{ 
	memset(vis, 0, sizeof(vis));
	
	queue<int> q;
	for(int i=1; i<=n; i++)
	{
		q.push(i);
		vis[i] = true;		
	}

	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = false;
		
		for(int i=h[x]; i; i=nxt[i])
		{
			int y = to[i];
			if(dis[y] > dis[x] + w[i])
			{
				dis[y] = dis[x] + w[i];
				//如果某条路径边的数量>=n，表示有负环
				cnt[y] = cnt[x] + 1;
				if(cnt[y] >= n) return true;
				if(!vis[y])
				{
					q.push(y);
					vis[y] = true; 
				}
			}
		}
	}
	return false;
}

int main()
{	
	int T = 0;
	scanf("%d", &T);
	while(T--)
	{
		tot = 0;
		memset(h, 0, sizeof(h));
		memset(to, 0, sizeof(to));
		memset(nxt, 0, sizeof(nxt));
		memset(w, 0, sizeof(w));
		memset(cnt, 0, sizeof(cnt));
		
		int x = 0, y = 0, z = 0;
		scanf("%d%d%d", &n, &m, &s);
		for(int i=1; i<=m; i++)
		{
			scanf("%d%d%d", &x, &y, &z);
			addedge(x, y, z);
			addedge(y, x, z);
		}
		for(int i=1; i<=s; i++)
		{
			scanf("%d%d%d", &x, &y, &z);
			addedge(x, y, -z);
		}
		
		if(spfa()) printf("YES\n");
		else printf("NO\n");
	}

	return 0;
}

dfs写法

memset(dis, 0x3f, sizeof(dis));
dis[0] = 0;//起始点为0点
void spfa(int x)
{
	vis[x] = true;//标记是否在dfs中
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(dis[y] > dis[x] + w[i])
		{
			if(vis[y])//如果在dfs中，说明有负环
			{
				printf("No");
				exit(0);
			}
			dis[y] = dis[x] + w[i];
			spfa(y);
		}
	}
	vis[x] = false;
}

二维最短路

例题：提高题库 157.传送门

#include <bits/stdc++.h>
using namespace std;

const int maxn = 10010; 
const int maxm = 100010;
const int inf = 0x3f3f3f3f;

int n = 0, m = 0, k = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
int dis[maxn][25] = {};
bool vis[maxn][25] = {};
struct node
{
	int x, t, dis;
	node(){}
	node(int a, int b, int c) 
	{
		x = a;
		t = b;
		dis = c;
	}
	bool operator < (const node &nd) const
	{
		if(dis == nd.dis) return t > nd.t;
		return dis > nd.dis;
	}
};
priority_queue<node> q;

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	w[tot] = z;
	h[x] = tot;
}

//优先队列优化的二维spfa
void dij(int x)
{
	memset(dis, 0x3f, sizeof(dis));
	dis[x][0] = 0;
	 
	q.push(node(x, 0, 0));
	vis[x][0] = true;
	
	while(q.size())
	{
		x = q.top().x;
		int t = q.top().t;
		q.pop(); 
		vis[x][t] = true;
		
		for(int i=h[x]; i; i=nxt[i])
		{
			int y = to[i];
			
			//不用传送门
			if(!vis[y][t] && dis[y][t] > dis[x][t] + w[i])
			{
				dis[y][t] = dis[x][t] + w[i];
				if(!vis[y][t]) q.push(node(y, t, dis[y][t]));
			}
			//用传送门
			if(t < k) 
			{
				if(!vis[y][t+1] && dis[y][t+1] > dis[x][t])
				{
					dis[y][t+1] = dis[x][t];
					if(!vis[y][t+1]) q.push(node(y, t+1, dis[y][t+1]));	
				}
			} 
		} 
	}
}

int main()
{	
	int x = 0, y = 0, z = 0;
	scanf("%d%d%d", &n, &m, &k);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &x, &y, &z);
		addedge(x, y, z);
		addedge(y, x, z);
	}
	
	dij(1);
	int ans = 0x7fffffff;
	for(int i=0; i<=k; i++)
	{
		ans = min(ans, dis[n][k]);
	}
	printf("%d", ans);

	return 0;
}

最小生成树

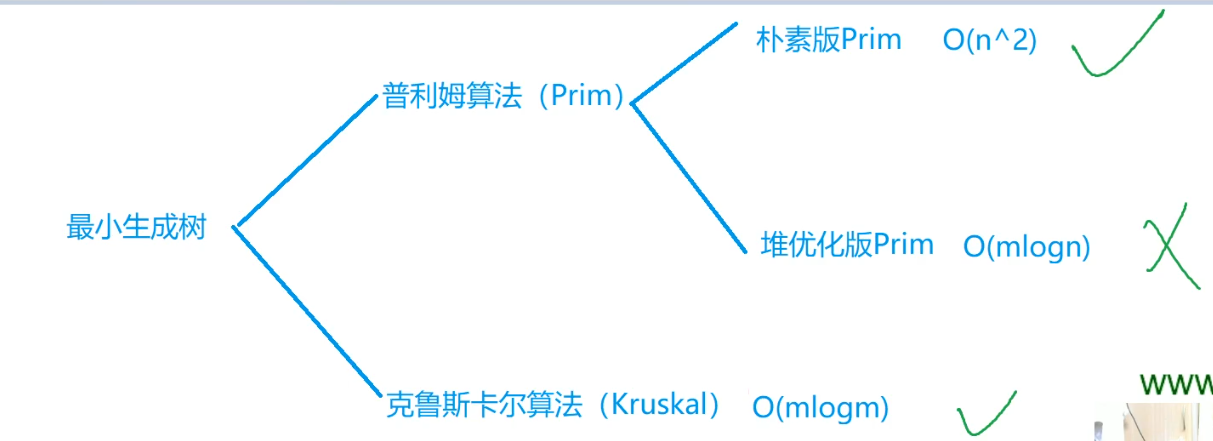
朴素版prim算法

时间复杂度\(O(n^2)\)，可以用二叉堆优化到\(O(mlogn)\)。
但用二叉堆优化不如直接用Kruskal算法更加方便。因此，Prim主要用于稠密图，尤其是完全图的最小生成树的求解
例题：提高题库 175.最优布线问题

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110; 

int n = 0; //n表示点数
//g[][]邻接矩阵存图，d[]存储其他点到当前最小生成树的距离
int g[maxn][maxn] = {}, d[maxn] = {}, ans = 0;
bool vis[maxn] = {};	//存储每个点是否已经在生成树中

void prim()
{
	memset(d, 0x3f, sizeof(d));
	memset(vis, 0, sizeof(vis));
	d[1] = 0;
	
	for(int i=1; i<n; i++)
	{
		//找到距离已确定点集合距离最短的点x
		int x = 0;
		for(int j=1; j<=n; j++)
		{
			if(!vis[j] && (x==0 || d[x]>d[j])) x = j;
		}
		vis[x] = true;
		//更新x点到与其相连的点的距离，即更新其他点到已确定点集合的距离
		for(int j=1; j<=n; j++)
		{
			if(!vis[j]) d[j] = min(d[j], g[x][j]);
		}
	}
}

int main()
{
	scanf("%d", &n);
	for(int i=1; i<=n; i++)
	{
		for(int j=1; j<=n; j++)
		{
			scanf("%d", &g[i][j]);
		} 
	}
	
	prim();
	for(int i=1; i<=n; i++) ans += d[i];
	printf("%d", ans);

	return 0;
}

堆优化prim算法

写法复杂，基本用不到

Kruskal

时间复杂度\(O(mlogm)\)
例题：提高题库 176.局域网

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110; 
const int maxm = maxn * maxn;

int n = 0, m = 0; //n表示点数,m表示边数
int fa[maxn] = {}, ans = 0, sum = 0;
struct node
{
	int x, y, z;
	bool operator < (const node &nd) const
	{
		return z < nd.z;
	}
}e[maxm];

int findset(int x)
{
	if(fa[x] != x) fa[x] = findset(fa[x]);
	return fa[x];
}

void Kruskal()
{
	int t = 0;
	//按边权从小到大排序
	sort(e+1, e+1+m);	
	//并查集初始化
	for(int i=1; i<=n; i++) fa[i] = i;
	//求最小生成树
	for(int i=1; i<=m; i++)
	{
		int fx = findset(e[i].x);
		int fy = findset(e[i].y);
		if(fx == fy) continue;
		fa[fy] = fx;
		ans += e[i].z;

		t++;
		if(t == n-1) break;
	}
}

int main()
{
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d", &e[i].x, &e[i].y, &e[i].z);
		sum += e[i].z;
	}
	
	Kruskal();
	printf("%d", sum - ans);
	
	return 0;
}

拓扑排序

定义： 在一个\(DAG\)（有向无环图）中，将图中的顶点以线性方式进行排序，使得对于任何的顶点\(u\)到\(v\)的有向边\((u,v)\)，都可以有\(u\)在\(v\)的前面。
目标： 将所有节点排序，使得排在前面的节点不能依赖于排在后面的节点。
时间复杂度: \(O(n+m)\)，n表示点数，m表示边数
样例：
给定一个\(DAG\)，求出其拓扑排序

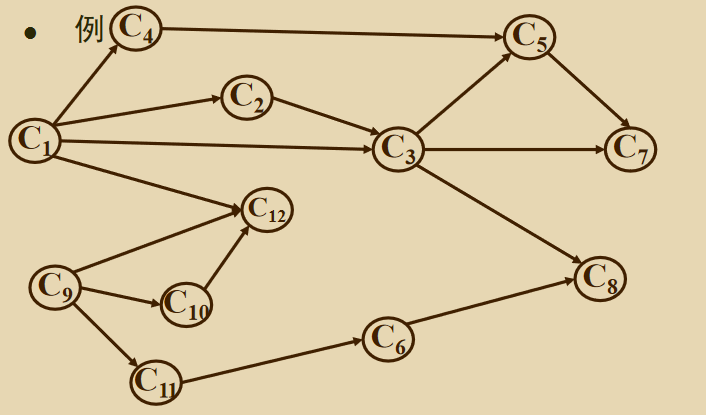
上图的拓扑序列可能是下面两种：
(C1, C2, C3, C4, C5, C7, C9, C10, C11, C6, C12, C8)
(C9, C10, C11, C6, C1, C12, C4, C2, C3, C5, C7, C8)
注意： 一个\(DAG\)的拓扑序列不唯一，与存图顺序有关，只要满足拓扑排序的定义即可
拓扑排序与\(bfs\)：
1、\(bfs\)可用于有向图或无向图，有环或无环
2、拓扑排序只能把入度为\(0\)的点作为起点，\(bfs\)可以把任意点作为起点
3、因此拓扑排序可以认为是一种特殊的\(bfs\)

int in[maxn] = {};	//存储某个节点的入度

bool topsort()
{
	int cnt = 0;	//记录经过的节点数量
	queue<int> q;
	
	//将入度为0的节点入队
	for(int i=1; i<=n; i++) 
	{
		if(in[i] == 0) q.push(i); 	 
	}
	
	while(!q.empty())
	{
		int x = q.front();
		q.pop(); 
		cnt++;
		
		for(int i=h[x]; i; i=nxt[i])
		{
			int y = to[i]; 
			in[y]--;
			if(in[y] == 0) q.push(y); 
		}
	}
	if(cnt == n) return true;
	return false;
}

例题：P262 家谱树

#include <bits/stdc++.h>
using namespace std;

const int maxn = 110;
const int maxm = maxn*maxn;

int n = 0;
int head[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
queue<int> q;
int v[maxn] = {};
int in[maxn] = {};

void addedge(int x, int y)
{
	nxt[++tot] = head[x];
	to[tot] = y; 
	head[x] = tot; 
}

void tpsort()
{
	for(int i=1; i<=n; i++) 
	{
		if(in[i] == 0) q.push(i);
	}
	
	while(q.size())
	{
		int x = q.front();
		q.pop();
		printf("%d ", x);
		for(int i=head[x]; i; i=nxt[i])
		{
			int y = to[i];
			in[y]--;
			if(in[y] == 0) q.push(y);
		}
	}
}

int main()
{
	int x = 0;
	
	scanf("%d", &n);
	for(int i=1; i<=n; i++)
	{
		while(1)
		{
			scanf("%d", &x);
			if(x == 0) break;
			addedge(i, x);
			in[x]++;
		}
	}

	tpsort();

	return 0;
} 

二分图

差分约束

判断是否合法

例题：提高题库 183.小K的农场

#include <bits/stdc++.h>
using namespace std;

const int maxn = 10010; 
const int maxm = 30010;

int n = 0, m = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, w[maxm] = {}, tot = 0;
bool vis[maxn] = {};
int dis[maxn] = {};

void addedge(int x, int y, int z)
{
	to[++tot] = y;
	w[tot] = z;
	nxt[tot] = h[x];
	h[x] = tot;
}

//dfs版spfa
void spfa(int x)
{
	vis[x] = true;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(dis[y] > dis[x] + w[i])
		{
			if(vis[y])
			{
				printf("No");
				exit(0);
			}
			dis[y] = dis[x] + w[i];
			spfa(y);
		}
	}
	vis[x] = false;
}

int main()
{ 
	int p = 0, a = 0, b = 0, c = 0;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d", &p);
		if(p == 1)
		{
			scanf("%d%d%d", &a, &b, &c);
			addedge(a, b, -c);
		}
		else if(p == 2)
		{
			scanf("%d%d%d", &a, &b, &c);
			addedge(b, a, c);
		}
		else
		{
			scanf("%d%d", &a, &b);
			addedge(b, a, 0);
			addedge(a, b, 0);
		}		
	}
 
	//建立超级源点
	for(int i=1; i<=n; i++) addedge(0, i, 0);
	
	//判断有无负环
	memset(dis, 0x3f, sizeof(dis));
	dis[0] = 0;
	spfa(0);
	printf("Yes");
} 

求最小值

最近公共祖先（LCA）

倍增法

倍增法为在线算法
例题：提高题库 315.Distance Queries 距离咨询

#include <bits/stdc++.h>
using namespace std;
 
const int maxn = 40010;
const int maxm = 80010;
 
int n = 0, m = 0, q = 0; 
int h[maxn] = {}, nxt[maxm] = {}, to[maxm] = {}, w[maxm] = {}, tot = 0;
int f[maxn][30] = {}, dis[maxn] = {}, dep[maxn] = {}; 
 
void addedge(int x, int y, int z)
{
	to[++tot] = y;
	w[tot] = z;
	nxt[tot] = h[x];
	h[x] = tot;
}

//①该题中任意两个农场之间都有且只有一条路径
//所以可以指定任意一个点为根节点
//并且只要dfs的过程中更新路径，该路径即为两点间的距离
//②dfs的过程中可以顺便维护节点深度
void dfs(int x, int fa)
{
	dep[x] = dep[fa] + 1;
	f[x][0] = fa;
	
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(y == fa) continue;
		dis[y] = dis[x] + w[i];
		
		dfs(y, x);
	}
}

//倍增法求lca
int lca(int x, int y)
{
	if(dep[x] < dep[y]) swap(x, y);
	
	//x和y跳到同一深度
	int d = dep[x] - dep[y];
	for(int i=0; i<30; i++)
	{
		if(d & (1<<i)) x = f[x][i];
	}
	
	if(x == y) return x;
	
	//x和y同时往上跳
	for(int i=29; i>=0; i--)
	{
		if(f[x][i] != f[y][i])
		{
			x = f[x][i];
			y = f[y][i];
		}
		if(f[x][0] == f[y][0]) break;
	}
	
	return f[x][0];
}
 
int main()
{ 
	int x = 0, y = 0, z = 0;
	char c;
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d%d %c", &x, &y, &z, &c);
		addedge(x, y, z);
		addedge(y, x, z);	
	}
	
	dfs(1, 0);
	
	//ST表初始化
	for(int j=1; j<30; j++)
	{
		for(int i=1; i<=n; i++)
		{
			f[i][j] = f[f[i][j-1]][j-1];
		}
	}
	
	scanf("%d", &q);
	while(q--)
	{
		scanf("%d%d", &x, &y);
		
		int t = lca(x, y);
		printf("%d\n", dis[x] + dis[y] - 2 * dis[t]);
	}
	 
	return 0;
} 

tarjan算法求lca

简介： tarjan算法为离线算法，需要使用并查集记录某个节点的祖先节点
主要思路： 首先初始化每个节点的祖先节点为自身，任选一个节点进行\(dfs\)，遍历完某个节点及其子节点后，将该点的父亲节点设置为该点的祖先节点，然后查询和这个点相关的所有询问，当另一端点\(v\)已经遍历过时，该端点\(v\)的祖先节点，即这两个点的最近公共祖先（\(lca\)）。
具体实现：
1、保存查询信息时，注意双向，即\(u->\)和\(v->u\)都要保存
2、初始化并查集，将每个点的祖先设置为其自身
3、开始\(dfs\)，遍历完每个节点即其子节点后，将该点的祖先节点设置为其父节点
4、遍历完某个点\(u\)的所有子节点后，开始查询与\(u\)点相关的询问，假设两个点为\((u, v)\),则可能出现以下情况
①\(v\)还没有遍历过。直接跳过，等待遍历到\(v\)时，再找\(u\)
②\(v\)为\(u\)的子节点。此时找\(v\)的祖先节点，祖先节点一定是\(u\)，即他们的\(lca\)。
③\(v\)和\(u\)属于不同的子树。此时\(v\)和\(u\)一定处于一棵大的子树中，找\(v\)的祖先节点，就是该大子树的根节点，即他们的\(lca\)。
5、最后输出结果
时间复杂度： \(O(mα(m+n,n)+n)\)，可近似认为是\(O(m+n)\)
例题： LG3379 【模板】最近公共祖先（LCA）

#include <bits/stdc++.h>
using namespace std;

const int maxn = 5e5 + 10;
const int maxm = 5e5 + 10;

int n = 0, m = 0, root = 0;
int h[maxn] = {}, to[maxn<<1] = {}, nxt[maxn<<1] = {}, tot = 0;
struct node
{
	int v, idx;			//指向的点和该询问的位置
};
vector<node> qry[maxn];	//存储查询信息
int fa[maxn] = {};		//并查集变量
int ans[maxm] = {};		//存储最终的答案
bool vis[maxn] = {};	//存储该节点是否已访问过

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

//找x的祖先
int findset(int x)
{
	if(x == fa[x]) return fa[x];
	return fa[x] = findset(fa[x]);
}

//求lca
void dfs(int x)
{
	int y = 0;
	
	vis[x] = true;
	for(int i=h[x]; i; i=nxt[i])
	{
		y = to[i];
		if(vis[y]) continue;
		
		dfs(y);
		fa[y] = x;
	}
	
	for(auto nd : qry[x])
	{
		if(vis[nd.v])
		{
			ans[nd.idx] = findset(nd.v);
		}
	}
}

int main() 
{ 
	int x = 0, y = 0;
	
	scanf("%d%d%d", &n, &m, &root);
	for(int i=1; i<n; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		qry[x].push_back({y, i});
		qry[y].push_back({x, i});
	}
	
	for(int i=1; i<=n; i++) fa[i] = i;
	dfs(root);
	for(int i=1; i<=m; i++) printf("%d\n", ans[i]);

	return 0;
}  

树链剖分

重链剖分

例题

例题：洛谷： P3384 【模板】重链剖分/树链剖分

#include <bits/stdc++.h>
using namespace std;
 
#define lson (rt << 1)
#define rson (rt << 1 | 1)
 
const int maxn = 1e5 + 10, maxm = 1e5 + 10;

//r:根节点  p:模数
int n = 0, m = 0, r = 0, p = 0;
int a[maxn] = {};
//邻接链表变量
int h[maxn] = {}, nxt[maxn<<1] = {}, to[maxn<<1] = {}, tot = 0;
//重链剖分变量
//fa(x) 表示节点 x 在树上的父亲
//dep(x) 表示节点 x 在树上的深度
//siz(x) 表示节点 x 的子树的节点个数
//son(x) 表示节点 x 的 重儿子
//top(x) 表示节点 x 所在 重链 的顶部节点（深度最小）
//dfn(x) 表示节点 x 的 DFS 序，也是其在线段树中的编号
//rnk(x) 表示 DFS 序所对应的节点编号，有 rnk(dfn(x))=x
//cnt 用来求dfs序
int fa[maxn] = {}, dep[maxn] = {}, siz[maxn] = {}, son[maxn] = {}, top[maxn] = {};
int dfn[maxn] = {}, rnk[maxn] = {}, cnt = 0;
//线段树变量
struct node
{
	int l, r, sum, lazy;
}tree[maxn<<2];

void pushup(int rt)
{
	tree[rt].sum = (tree[lson].sum + tree[rson].sum) % p;
}

//把当前节点rt的延迟标记下放到左右儿子
void pushdown(int rt)
{
	if(tree[rt].lazy)//此节点有延迟标记
	{
		int lz = tree[rt].lazy;
		tree[rt].lazy = 0;//记住要清零
		tree[lson].lazy = (tree[lson].lazy + lz) % p;
		tree[rson].lazy = (tree[rson].lazy + lz) % p;
		tree[lson].sum = (tree[lson].sum + lz * (tree[lson].r - tree[lson].l + 1) % p) % p;
		tree[rson].sum = (tree[rson].sum + lz * (tree[rson].r - tree[rson].l + 1) % p) % p;
	}
}

//建树
void Build(int rt, int l, int r)
{
	tree[rt].l = l;
	tree[rt].r = r;//节点信息初始化
	if(l == r)//到叶节点
	{
		tree[rt].sum = a[rnk[l]] % p;
		return;
	}
	
	int mid = (l + r) >> 1;
	Build(lson, l, mid);
	Build(rson, mid+1, r);
	
	pushup(rt);//子树建好后，回溯时更新父节点信息
}

void Update(int rt, int l, int r, int val)
{
	//更新区间完全覆盖节点表示的区间
	if(l<=tree[rt].l && tree[rt].r<=r)
	{
		tree[rt].lazy = (tree[rt].lazy + val) % p;
		tree[rt].sum = (tree[rt].sum + val * (tree[rt].r - tree[rt].l + 1) % p) % p;
		return;
	}
	
	//如果不能完全覆盖，此时需要向下递归，要下放标记
	pushdown(rt);
	int mid = (tree[rt].l + tree[rt].r) >> 1;
	if(l <= mid) Update(lson, l, r, val);
	if(r > mid) Update(rson, l, r, val);
	
	pushup(rt);
}

//当前节点为rt,要查询的区间是[l, r]
int Query(int rt, int l, int r)
{
	int ret = 0;
	//如果节点表示的区间是查询区间的真子集
	if(l<=tree[rt].l && tree[rt].r<=r)
	{
		return tree[rt].sum % p;
	}
	
	//如果不能完全覆盖，此时需要向下递归，要下放标记
	pushdown(rt);
	int mid = (tree[rt].l + tree[rt].r) >> 1;
	if(l <= mid) ret = (ret + Query(lson, l, r)) % p;
	if(r > mid) ret = (ret + Query(rson, l, r)) % p;
	return ret;
}

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

//求出 fa(x)，dep(x)，siz(x)，son(x)
void dfs1(int x)
{
	son[x] = -1;
	siz[x] = 1;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dep[y])
		{
			dep[y] = dep[x] + 1;
			fa[y] = x;
			dfs1(y);
			siz[x] += siz[y];
			if(son[x]==-1 || siz[y]>siz[son[x]]) son[x] = y;
		}
	}
}

//求出 top(x)，dfn(x)，rnk(x)
void dfs2(int x, int t)
{
	top[x] = t;
	cnt++;
	dfn[x] = cnt;
	rnk[cnt] = x;
	if(son[x] == -1) return;	//x为叶子节点
	dfs2(son[x], t);// 优先对重儿子进行 DFS，可以保证同一条重链上的点 DFS 序连续
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		//y为轻儿子时，单独开一条链，y为链顶端点
		if(y!=son[x] && y!=fa[x]) dfs2(y, y);	
	}
}

void add1(int x, int y, int val)
{
	//跳重链
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		Update(1, dfn[top[x]], dfn[x], val);
		x = fa[top[x]];
	}
	
	//已跳到同一条重链
	if(dep[x] > dep[y]) swap(x, y);
	Update(1, dfn[x], dfn[y], val);
}

int query1(int x, int y)
{
	int ret = 0;
	//跳重链
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		ret = (ret + Query(1, dfn[top[x]], dfn[x])) % p;
		x = fa[top[x]];
	}
	
	//已跳到同一条重链
	if(dep[x] > dep[y]) swap(x, y);
	ret = (ret + Query(1, dfn[x], dfn[y])) % p;
	return ret;
}

int main()
{   
//	freopen("P3384_11.in", "r", stdin);

	int op = 0, x = 0, y = 0, z = 0;
	scanf("%d%d%d%d", &n, &m, &r, &p);
	for(int i=1; i<=n; i++) scanf("%d", &a[i]);
	for(int i=1; i<n; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}

	//执行重链剖分,两遍 DFS 预处理出这些值，
	//第一次 DFS 求出 fa(x)，dep(x)，siz(x)，son(x) 
	dep[r] = 1;
	dfs1(r);
	//第二次 DFS 求出 top(x)，dfn(x)，rnk(x)。
	dfs2(r, r);

	//针对dfn序建树
	Build(1, 1, cnt);
	while(m--)
	{
		scanf("%d", &op);
		if(op == 1)
		{
			scanf("%d%d%d", &x, &y, &z);
			add1(x, y, z);
		}
		else if(op == 2)
		{
			scanf("%d%d", &x, &y);
			int ans = query1(x, y);
			printf("%d\n", ans);
		}
		else if(op == 3)
		{
			scanf("%d%d", &x, &z);
			Update(1, dfn[x], dfn[x]+siz[x]-1, z);
		}
		else if(op == 4)
		{
			scanf("%d", &x);
			int ans = Query(1, dfn[x], dfn[x]+siz[x]-1);
			printf("%d\n", ans);
		}
	}

	return 0;
} 

Tarjan

一些概念

无向连通图的搜索树：在无向连通图中任选一个节点出发进行深度优先遍历，每个点只访问一次。所有发生递归的边\((x,y)\)(换言之，从\(x\)到\(y\)是对\(y\)的第一次访问)构成一棵树，我们把他称为"无向连通图的搜索树"。

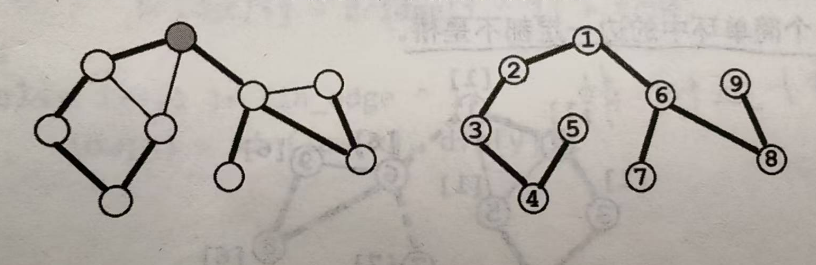
时间戳：在图的深度优先遍历过程中，按照每个节点第一次被访问的时间顺序，依次给予\(N\)个节点\(1\)~\(N\)的整数标记，该标记被称为“时间戳”，记为\(dfn[x]\)
追溯值： 设\(subtree(x)\)表示搜索树中以\(x\)为根的子树。\(low[x]\)定义为以下节点的时间戳的最小值
1、\(subtree(x)\)中的节点
2、通过1条不在搜索树上的边，能够到达\(subtree(x)\)的节点。
计算追溯值：
先令\(low[x]=dfn[x]\),然后考虑从\(x\)出发的每条边\((x, y)\)
1、树边，若在搜索树上\(x\)是\(y\)的父节点，则令\(low[x]=min(low[x],low[y])\)
2、非树边，若无向边\((x, y)\)不是搜索树上的边，则令\(low[x]=min(low[x],dfn[y])\)

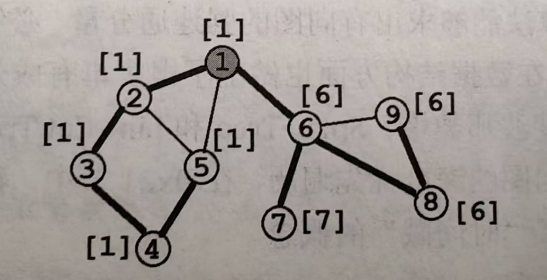
割边

割边或桥：对于无向图 \(G=(V, E)\),若对于\(e∈E\),从图中删去边\(e\)之后，\(G\)分裂成两个不相连的子图，则称\(e\)为\(G\)的割边或桥。
ps:树中所有边都是桥
概念：无向边\((x, y)\)是桥，当且仅当搜索树上存在\(x\)的一个子节点\(y\)，满足\(dfn[x]<low[y]\),即追溯不到更小的点
ps:桥一定是搜索树中的边，并且一个简单环中的边一定都不是桥

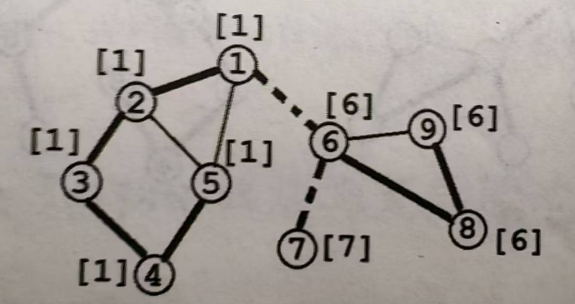
上图有两条割边，1->6和6->7

割边算法模板

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0; 
bool bridge[maxm] = {};

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void tarjan(int x, int in_edge)
{
	dfn[x] = low[x] = ++num;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dfn[y])	//树边
		{
			tarjan(y, i);
			low[x] = min(low[x], low[y]);
			
			//此时已经遍历完x的子节点，又回溯到了x 
			if(dfn[x] < low[y]) //说明经过(x,y)边，无法到达比x更早的点
			{
				//i和i^1是同一条边
				bridge[i] = bridge[i^1] = true;
			}
		}
		//i == (in_edge ^ 1)表示与i是同一条边
		//i != (in_edge ^ 1)说明是非树边
		else if(i != (in_edge ^ 1))
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
}

int main()
{	 
	int x = 0, y = 0;

	//这里是为了保证i和i^1是同一条边
	//这样边的编号从2开始，2/3为一对，4/5为一对，以此类推
	tot = 1;	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) tarjan(i, 0);
	}
	for(int i=2; i<tot; i++)
	{
		if(bridge[i])
		{
			printf("%d %d\n", to[i^1], to[i]);
		}
	}
	
	return 0;
} 

割点

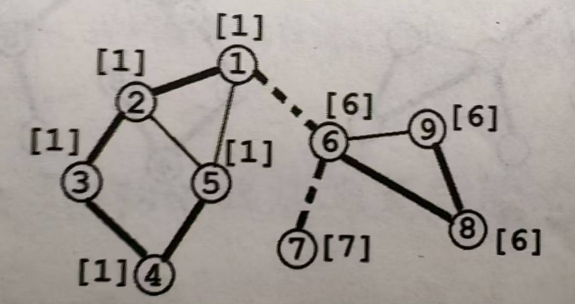
割点：对于无向图 \(G=(V, E)\),若对于\(x∈V\),从图中删去节点\(x\)以及所有与\(x\)关联的边之后，\(G\)分裂成两个或两个以上不相连的子图，则称\(x\)为\(G\)的割点。
ps:树中度为1的点（叶子结点）都不是割点，其他都是割点
条件：若\(x\)不是搜索树的根节点（深度优先遍历的起点），则\(x\)是割点当且仅当搜索树上存在\(x\)的一个子节点\(y\),满足：\(dfn[x]<=low[y]\)
特点：
1、若\(x\)是搜索树的根节点，则\(x\)是割点当且仅当搜索树上存在至少两个子节点\(y1,y2\)满足上述条件。
2、下面非空，即不能是叶子节点
3、上下只能通过\(x\)相通，即y子树不能追溯到比x更早的点
下图中共有两个割点，分别是时间戳为1和6的两个点

割点算法模板

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0;
int root = 0;  
bool cut[maxn] = {};
int cnt = 0;

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void tarjan(int x)
{
	dfn[x] = low[x] = ++num;
	int flag = 0;	//记录x有多少个不能回溯到x之前的子节点
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dfn[y])	//树边
		{
			tarjan(y);
			low[x] = min(low[x], low[y]);
			
			//此时已经遍历完x的子节点，又回溯到了x 
			if(dfn[x] <= low[y]) //y无法到达比x更早的点
			{
				flag++;
				if(x != root || flag > 1) 
				{
					//如果统计割点数量，这里要判断一下是否已标记
					//因为一个割点可能会被重复访问
					//下图中点6就会被访问两次
					if(!cut[x])
					{
						cut[x] = true;
						cnt++;			
					} 
				}
			}
		} 
		else
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
}

int main()
{	 
	int x = 0, y = 0;
 
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		if(x == y) continue;
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) 
		{
			root = i;	//方便后面判断是否为根节点
			tarjan(i);
		}
	}
	for(int i=1; i<=n; i++)
	{
		if(cut[i]) printf("%d ", i); 
	}
	printf("are cut-vertexes");
	
	return 0;
} 

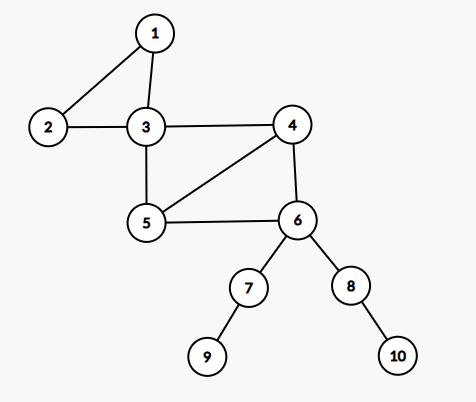
无向图的双连通分量

点双连通图：若一张无向连通图不存在割点，则称它为“点双连通图”
边双连通图：若一张无向连通图不存在桥，则称他为“边双连通图”
点双连通分量：无向图的极大点双连通子图被称为“点双连通分量”\(v-DCC\)
边双连通分量：无向连通图的极大边双连通子图被称为“边双连通分量”简称\(e-DCC\)
一张无向连通图是“点双连通图”，当且仅当满足下列两个条件之一：
1、图的顶点数不超过2。（ps：意思是当一个图仅有1个或2个顶点时，一定是点双）
2、图中任意两点都同时包含在至少一个简单环中。（ps：“简单环”指的是不自交的环，也就是我们通常画出的环）

边双连通分量（e-DCC）的求法模板：

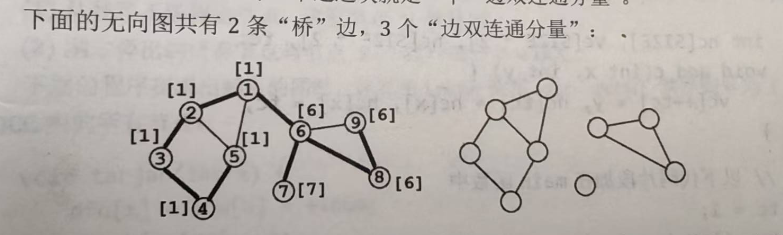
算法：先用\(Tarjan\)算法标记出所有的桥边。然后，再对整个无向图执行一次深度优先遍历(遍历的过程中不访问桥边),划分出每个连通块。
下面的代码在\(Tarjan\)求桥的基础上，计算出数组\(c\)，\(c[x]\)表示节点\(x\)所属的“边双连通分量”的编号

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0; 
bool bridge[maxm] = {};
int c[maxn] = {}, dcc = 0;

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void tarjan(int x, int in_edge)
{
	dfn[x] = low[x] = ++num;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dfn[y])	//树边
		{
			tarjan(y, i);
			low[x] = min(low[x], low[y]);
			
			//此时已经遍历完y节点
			if(dfn[x] < low[y]) //说明经过(x,y)边，无法到达比x更早的点
			{
				//i和i^1是同一条边
				bridge[i] = bridge[i^1] = true;
			}
		}
		//i == (in_edge ^ 1)表示与i是同一条边
		//i != (in_edge ^ 1)说明是非树边
		else if(i != (in_edge ^ 1))
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
}

void dfs(int x)
{
	c[x] = dcc;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(c[y] || bridge[i]) continue;
		dfs(y);
	}
}

int main()
{	 
	int x = 0, y = 0;

	//这里是为了保证i和i^1是同一条边
	//这样边的编号从2开始，2/3为一对，4/5为一对，以此类推
	tot = 1;	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) tarjan(i, 0);
	}
	
	for(int i=1; i<=n; i++)
	{
		if(!c[i])
		{
			++dcc;
			dfs(i);
		}
	}
	printf("There are %d e-DCCs.\n", dcc);
	for(int i=1; i<=n; i++)
	{
		printf("%d belongs to DCC %d.\n", i, c[i]);
	}
	
	return 0;
}  

e-DCC的缩点模板：

把每个\(e-DCC\)看做一个节点，把桥边\((x, y)\)看做连接编号为\(c[x]\)和\(c[y]\)的\(e-DCC\)对应节点的无向边，会产生一棵树(若原来的无向图不连通，则产生森林)。这种把\(e-DCC\)收缩为一个节点的方法就称为“缩点”。
下面的代码在\(Tarjan\)求桥、求\(e-DCC\)的参考程序基础上，把\(e-DCC\)缩点，构成一棵新的树(或森林)，存储在另一个邻接表中

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存原图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0; 
bool bridge[maxm] = {};
int c[maxn] = {}, dcc = 0;
//存缩点后的图
int hc[maxn] = {}, toc[maxm] = {}, nxtc[maxn] = {}, totc = 0;

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void addedge_c(int x, int y)
{
	toc[++totc] = y;
	nxtc[totc] = hc[x];
	hc[x] = totc;
}

void tarjan(int x, int in_edge)
{
	dfn[x] = low[x] = ++num;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dfn[y])	//树边
		{
			tarjan(y, i);
			low[x] = min(low[x], low[y]);
			
			//此时已经遍历完y节点
			if(dfn[x] < low[y]) //说明经过(x,y)边，无法到达比x更早的点
			{
				//i和i^1是同一条边
				bridge[i] = bridge[i^1] = true;
			}
		}
		//i == (in_edge ^ 1)表示与i是同一条边
		//i != (in_edge ^ 1)说明是非树边
		else if(i != (in_edge ^ 1))
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
}

void dfs(int x)
{
	c[x] = dcc;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(c[y] || bridge[i]) continue;
		dfs(y);
	}
}

int main()
{	 
	int x = 0, y = 0;

	//这里是为了保证i和i^1是同一条边
	//这样边的编号从2开始，2/3为一对，4/5为一对，以此类推
	tot = 1;	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) tarjan(i, 0);
	}
	
	for(int i=1; i<=n; i++)
	{
		if(!c[i])
		{
			++dcc;
			dfs(i);
		}
	}
	
	printf("There are %d e-DCCs.\n", dcc);
	for(int i=1; i<=n; i++)
	{
		printf("%d belongs to DCC %d.\n", i, c[i]);
	}
	
	totc = 1;
	for(int i=2; i<=tot; i++)
	{
		//第i条边为x->y,第i^1条边为y->x
		int x = to[i^1], y = to[i];
		if(c[x] == c[y]) continue;
		addedge_c(c[x], c[y]);
	}
	
	printf("缩点之后的森林，点数%d,边数%d\n", dcc, totc / 2);
	for(int i=2; i<totc; i+=2)
	{
		printf("%d %d\n", toc[i^1], toc[i]);
	}
	
	return 0;
}  

点双连通分量（v-DCC）的求法模板：

定义：
1、若某个节点为孤立点，则它自己单独构成一个\(v-DCC\)。
2、除了孤立点外，点双连通分量的大小至少为2.
3、根据\(v-DCC\)定义中的“极大”性，虽然桥不属于任何\(e-DCC\)，但是割点可能属于多个\(v-DCC\)。

下面的无向图共有2个割点，4个“点双连通分量”

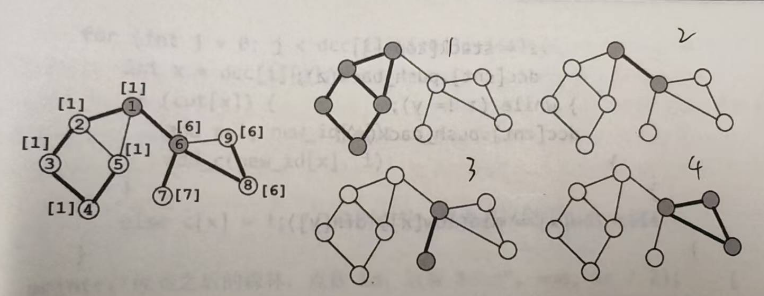
算法简介：
1、当一个节点第一次被访问时，把该节点入栈
2、当割点判定法则中的条件\(dfn[x]<=low[y]\)成立时，无论x是否为根，都要
(1)从栈顶不断弹出节点，直至节点y被弹出
(2)刚才弹出的所有节点与节点\(x\)一起构成一个\(v-DCC\)。
下面的程序在求割点的同时，计算出\(vector\)数组\(dcc\)，\(dcc[i]\)保存编号为\(i\)的\(v-DCC\)中的所有节点

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0;
int root = 0;  
bool cut[maxn] = {};	//cut[x]表示x是否为割点
//cnt表示点双的数量
int stk[maxn] = {}, top = 0, cnt = 0;
vector<int> dcc[maxn];	//dcc[x]表示第x个点双中包含的节点

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void tarjan(int x)
{
	dfn[x] = low[x] = ++num;
	int flag = 0;	//记录x有多少个不能回溯到x之前的子节点
	stk[++top] = x;
	
	if(x == root && h[x] == 0)	//孤立点
	{
		dcc[++cnt].push_back(x);
		return;
	}
	 
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dfn[y])	//树边
		{
			tarjan(y);
			low[x] = min(low[x], low[y]);
			
			//此时已经遍历完x的子节点，又回溯到了x 
			if(dfn[x] <= low[y]) //y无法到达比x更早的点
			{
				flag++;
				if(x != root || flag > 1) cut[x] = true;
				cnt++;
				int z = 0;
				do
				{
					z = stk[top--];
					dcc[cnt].push_back(z);
				}while(z != y);
				dcc[cnt].push_back(x);
			}
		} 
		else
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
}

int main()
{	 
	int x = 0, y = 0;
 
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		if(x == y) continue;
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) 
		{
			root = i;	//方便后面判断是否为根节点
			tarjan(i);
		}
	}
	for(int i=1; i<=n; i++)
	{
		if(cut[i]) printf("%d ", i); 
	}
	printf("are cut-vertexes");
	
	for(int i=1; i<=cnt; i++)
	{
		printf("v-DCC #%d:", i);
		for(int j=0; j<dcc[i].size(); j++)
		{
			printf(" %d", dcc[i][j]);
		}
		printf("\n");
	}
	
	return 0;
}  

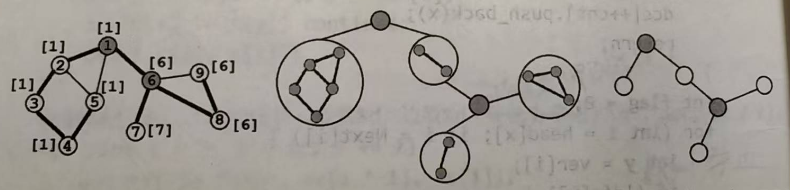
v-DCC的缩点模板：

v-DCC的缩点比e-DCC要复杂一些——因为一个割点可能属于多个v-DCC。
设图中共有p个割点和t个v-DCC。我们建立一张包含p+t个节点的新图，把每个v-DCC和每个割点都作为新图中的节点，并在每个割点与包含它的所有v-DCC之间连边。
容易发现，这张新图其实是一棵树（或森林），如下图所示：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0;
int root = 0;  
bool cut[maxn] = {}, c[maxn] = {};	//cut[x]表示x是否为割点,c[x]表示x属于哪个v-DCC
//cnt表示点双的数量
int stk[maxn] = {}, top = 0, cnt = 0;
vector<int> dcc[maxn];	//dcc[x]表示第x个点双中包含的节点
int new_id[maxn] = {};	//new_id[x]表示割点x的新编号
int hc[maxn] = {}, toc[maxm] = {}, nxtc[maxm] = {}, totc = 0;

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void addedge_c(int x, int y)
{
	toc[++totc] = y;
	nxtc[totc] = h[x];
	hc[x] = totc;
}

void tarjan(int x)
{
	dfn[x] = low[x] = ++num;
	int flag = 0;	//记录x有多少个不能回溯到x之前的子节点
	stk[++top] = x;
	
	if(x == root && h[x] == 0)	//孤立点
	{
		dcc[++cnt].push_back(x);
		return;
	}
	 
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dfn[y])	//树边
		{
			tarjan(y);
			low[x] = min(low[x], low[y]);
			
			//此时已经遍历完x的子节点，又回溯到了x 
			if(dfn[x] <= low[y]) //y无法到达比x更早的点
			{
				flag++;
				if(x != root || flag > 1) cut[x] = true;
				cnt++;
				int z = 0;
				do
				{
					z = stk[top--];
					dcc[cnt].push_back(z);
				}while(z != y);
				dcc[cnt].push_back(x);
			}
		} 
		else
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
}

int main()
{	 
	int x = 0, y = 0;
 
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		if(x == y) continue;
		addedge(x, y);
		addedge(y, x);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) 
		{
			root = i;	//方便后面判断是否为根节点
			tarjan(i);
		}
	}
	for(int i=1; i<=n; i++)
	{
		if(cut[i]) printf("%d ", i); 
	}
	printf("are cut-vertexes");
	 
	for(int i=1; i<=cnt; i++)
	{
		printf("v-DCC #%d:", i);
		for(int j=0; j<dcc[i].size(); j++)
		{
			printf(" %d", dcc[i][j]);
		}
		printf("\n");
	}
	
	//给每个割点一个新的编号(编号从cnt+1开始)
	num = cnt;
	for(int i=1; i<=n; i++)
	{
		if(cut[i]) new_id[i] = ++num;
	}
	//建新图，从每个v-DCC到它包含的所有割点连边
	totc = 1;
	for(int i=1; i<=cnt; i++)
	{
		for(int j=0; j<dcc[i].size(); j++)
		{
			int x = dcc[i][j];
			if(cut[x])
			{
				addedge_c(i, new_id[x]);	//i就是该v-DCC的编号，连线
				addedge_c(new_id[x], i);
			}
			else c[x] = i;
		}
	}
	
	printf("缩点之后的森林，点数%d，边数%d\n", num, totc / 2);
	printf("编号1~%d的为原图的v-DCC，编号>%d的为原图割点\n", cnt, cnt);
	for(int i=2; i<totc; i+=2)
	{
		printf("%d %d\n", toc[i^1], toc[i]);
	}
	
	return 0;
}  

有向图连通性

流图：给定有向图\(G=(V, E)\)，若存在\(r∈V\),满足从\(r\)出发能够到达V中所有的点，则称\(G\)是一个“流图”，记为\((G, r)\),其中\(r\)称为流图的源点
流图\((G, r)\)的搜索树：在一个流图\((G, r)\)上从\(r\)出发进行深度优先遍历，每个点只访问一次。所有发生递归的边\((x, y)\)(换言之，从\(x\)到\(y\)是对\(y\)的第一次访问)构成一棵以\(r\)为根的数，我们把他称为流图\((G, r)\)的搜索树
时间戳： 在深度优先遍历的过程中，按照每个节点第一次被访问的时间顺序，一次给予流图中的\(N\)个节点1~\(N\)的整数标记，该标记被称为时间戳，记为\(dfn[x]\)
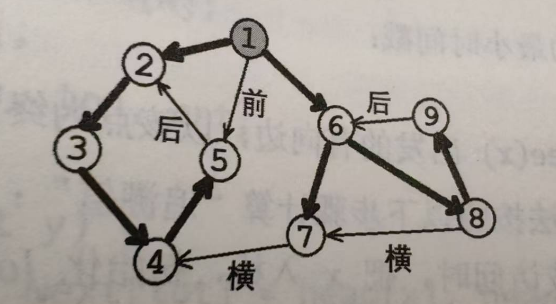
流图中的每条有向边\((x, y)\)必然是以下四种之一：
1、树枝边：指搜索树中的边，即\(x\)是\(y\)的父节点
2、前向边：指搜索树中\(x\)是\(y\)的祖先节点(没啥用，因为搜索树上本来就存在\(x\)到\(y\)的路径)
3、后向边：指搜索树中\(y\)是\(x\)的祖先节点(非常有用，因为它可以和搜索树上从\(y\)到\(x\)的路径一起构成环)
4、横叉边：指除了以上三种情况之外的边，他一定满足\(dfn[y]<dfn[x]\)（视情况而定，如果从\(y\)出发能找到一条路径回到\(x\)的祖先节点，那么\((x, y)\)就是有用的）

强连通图：给定一张有向图，若对于图中任意两个节点\(x,y\),既存在从\(x\)到\(y\)的路径，也存在从\(y\)到\(x\)的路径，则称该有向图是“强连通图”
强联通分量：有向图的极大强联通子图被称为“强联通分量”，简称“SCC”
追溯值: 设\(subtree(x)\)表示流图的搜索树中以\(x\)为根的子树。\(x\)的追溯值\(low[x]\)定义为满足以下条件的节点的最小时间戳：
1、该点在栈中（即遍历过该点）
2、存在一条从\(subtree(x)\)出发的有向边，以该点为终点（即存在横向边或后向边能到达该点）
追溯值的计算：
1、当节点\(x\)第一次被访问时，把\(x\)入栈，初始化\(low[x]=dfn[x]\)
2、扫描从\(x\)出发的每条边\((x, y)\)
(1)若\(y\)没被访问过，则说明\((x, y)\)是树枝边，递归访问\(y\)，从\(y\)回溯之后，令\(low[x]=min(low[x], low[y])\)
(2)若\(y\)被访问过并且\(y\)在栈中，则说明\((x, y)\)是后向边，则令\(low[x]=min(low[x], dfn[y])\)
求强连通分量： 从\(x\)回溯之前，判断是否有\(low[x]=dfn[x]\)（说明\(subtree(x)\)追溯不到更高点了，此时出栈，则在最高点时出栈）。若成立，则不断从栈中弹出节点，直至\(x\)出栈。

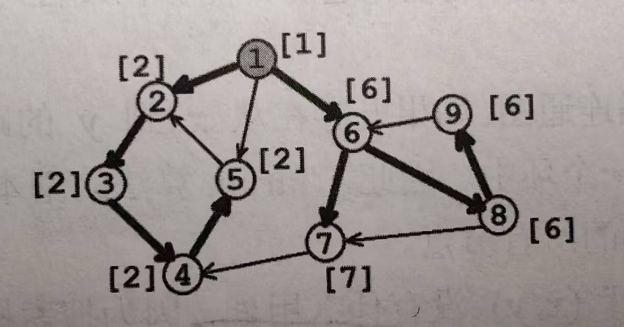
上图共有4个强联通分量(scc),分别是（2,3,4,5）（7）（6,8,9）（1）
强联通分量判定法则：
若从\(x\)回溯前，有\(low[x]=dfn[x]\)成立，则栈中从\(x\)到栈顶的所有节点构成一个强联通分量

scc算法模板：

下面的程序实现了\(Tarjan\)算法，求出数组\(c\)，其中\(c[x]\)表示\(x\)所在的强连通分量的编号。另外，它还求出了\(vector\)数组\(scc\),\(scc[i]\)记录了编号为\(i\)的强连通分量中的所有节点。整张图同有\(cnt\)个强连通分量

#include <bits/stdc++.h>
using namespace std;

const int maxn = 100010;
const int maxm = 1000010;

int n = 0, m = 0;
//存图
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;
//dfn:时间戳   low:追溯值
int dfn[maxn] = {}, low[maxn] = {}, num = 0;
//stk:数组表示栈
//ins[x]:表示x是否在栈中
//c[x]:表示x属于哪个scc
int stk[maxn] = {}, top = 0, ins[maxn] = {}, c[maxn] = {}, cnt = 0;
//scc[x]:表示第x个scc中的点
vector<int>scc[maxn] = {};

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void tarjan(int x)
{
	int y = 0;
	dfn[x] = low[x] = ++num;	//初始是时间戳等于追溯值
	stk[++top] = x;
	ins[x] = 1;
	
	for(int i=h[x]; i; i=nxt[i])
	{
		y = to[i];
		if(!dfn[y])
		{
			tarjan(y);
			//树枝边，回溯是更新low[x]
			low[x] = min(low[x], low[y]);
		}
		else if(ins[y])	//在栈中，即表示之前访问过
		{
			//横向边或后向边
			low[x] = min(low[x], dfn[y]);
		}
	}
	
	if(dfn[x] == low[x])
	{ 
		cnt++;
		do
		{
			y = stk[top--];	//出栈
			ins[y] = 0;
			c[y] = cnt;	//标记该点属于哪个scc
			scc[cnt].push_back(y);	//将该点加入对应scc的容器
		}while(x != y);
	}
}

int main()
{	 
	int x = 0, y = 0;

	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
	}
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) tarjan(i);
	}
	
	return 0;
}

scc缩点模板：

#include <bits/stdc++.h>
using namespace std;

/*
1、求出该图中的强联通分量scc
2、将scc进行缩点后，形成一个新图
*/

const int maxn = 500010;
const int maxm = 500010;

int n = 0, m = 0;
int h[maxn] = {}, to[maxm] = {}, nxt[maxm] = {}, tot = 0;	
int dfn[maxn] = {}, low[maxn] = {}, num = 0; 
int stk[maxn] = {}, top = 0, ins[maxn] = {}, cnt = 0, c[maxn] = {};
vector<int> scc[maxn] = {};
int hc[maxn] = {}, toc[maxm] = {}, nxtc[maxm] = {}, totc = 0;

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

void addedge_c(int x, int y)
{
	toc[++totc] = y;
	nxtc[totc] = hc[x];
	hc[x] = totc;
}

void tarjan(int x)
{
	int y = 0;
	dfn[x] = low[x] = ++num;
	stk[++top] = x;
	ins[x] = 1;
	
	for(int i=h[x]; i; i=nxt[i])
	{
		y = to[i];
		if(!dfn[y])
		{
			tarjan(y);
			
			low[x] = min(low[x], low[y]);
		}		
		else if(ins[y])
		{
			low[x] = min(low[x], dfn[y]);
		}
	}
	
	if(dfn[x] == low[x])
	{
		cnt++;
		do
		{
			y = stk[top--];
			ins[y] = 0;
			c[y] = cnt;
			scc[cnt].push_back(y);
		}while(x != y);
	}
}

int main()
{	 
	int x = 0, y = 0;
	
	scanf("%d%d", &n, &m);
	for(int i=1; i<=m; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
	}
	
	//tarjan求scc模板
	for(int i=1; i<=n; i++)
	{
		if(!dfn[i]) tarjan(i);
	}
	
	//缩点，建新图
	for(int x=1; x<=n; x++)
	{
		for(int i=h[x]; i; i=nxt[i])
		{
			y = to[i];
			if(c[x] == c[y]) continue;
			addedge_c(c[x], c[y]);
		}
	}
	
	return 0;
}  

树链剖分

重链剖分

概念

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。
具体来说，将整棵树剖分为若干条链，使它们组合成线性结构，然后用其他数据结构（如线段树、树状数组、分块）维护信息。

一些定义

重子节点：表示其子节点中子树最大的子节点。如果有多个子树最大的子节点，取其一。如果没有子节点，就无重子节点
轻子节点：表示剩余的所有子节点
重边：从该节点到其重子节点的边为重边
轻边：从该节点到其轻子节点的边为轻边
重链：若干条首尾衔接的重边构成重链
把落单的节点也当作重链，那么整棵树就被剖分成若干条重链

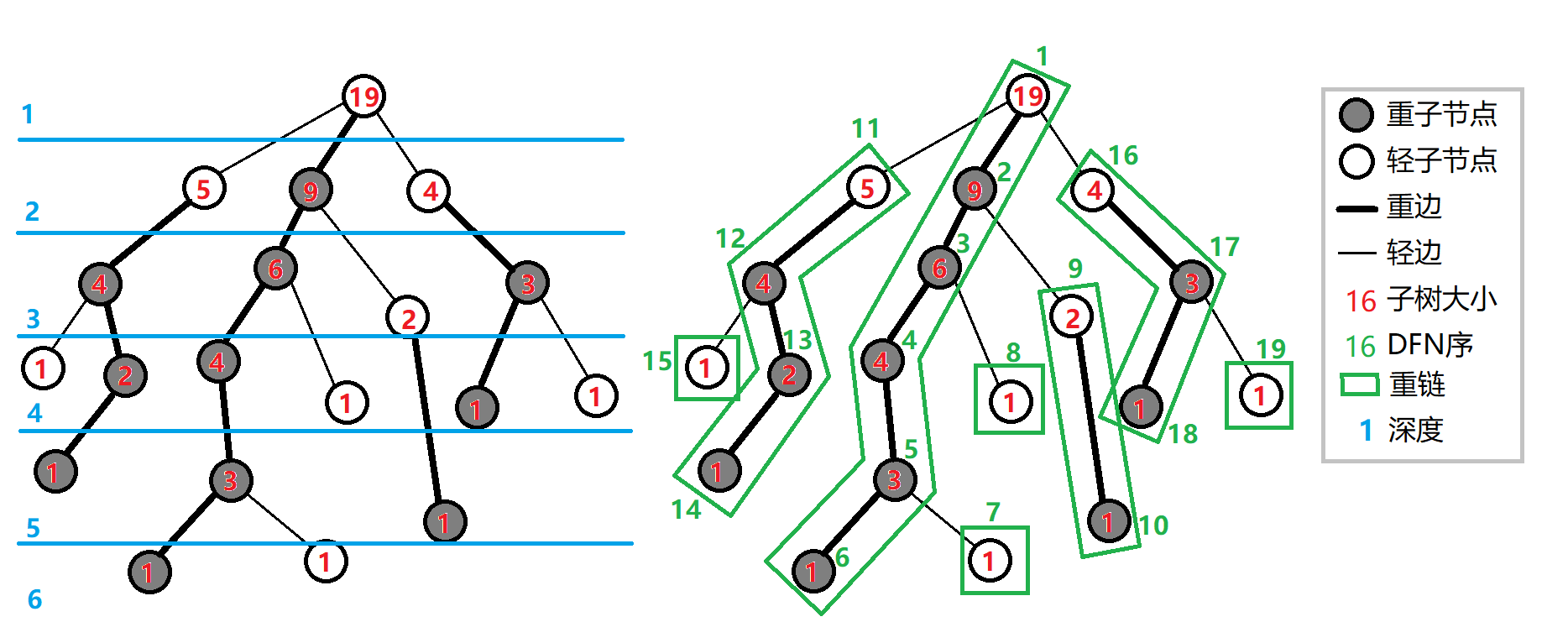
一些性质

1、当树的节点为\(n\)时，最多有\(n-1\)条重链(特殊的，当树只有1个节点时，只有1条重链)
2、树上每个节点都属于且仅属于一条重链
3、重链开头的节点只能是根节点或轻子节点
4、所有的重链将整棵树完全剖分
5、在剖分时，重边优先遍历，最后树的\(dfs\)序上，重链内的\(dfs\)序是连续的。按\(dfn\)排序后的序列即为剖分后的链。
6、一棵子树内的\(dfs\)序是连续的
7、当向下经过一条轻边时，所在子树的大小至少会除以2
8、对于树上的任意一条路径，都可以被拆分成不超过\(O(logn)\)条重链。

解释上面的性质：
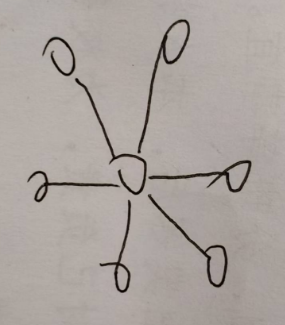
1、每条重链的末尾都是叶子节点，而叶子节点又只能属于一条重链，因此重链的条数等于叶子的数量，当树为星型结构时，重链最多,为\(n-1\)条

7、轻边\((u,v)\),\(size(v)<=size(u)/2\)
8、每增加一条重链，必定是通过轻边跳过去，所以重链的数量等于轻边的数量，而每经过一条轻边，点的数量至少会减少一半，所以最多经过\(logn\)条轻边，重链的数量最多也是\(logn\)。假如求\(x->y\)经过的重链条数，不用管\(lca\)，直接\(x\)当成根节点思考就可以。

应用

1、求lca
2、拆分成链，用数据结构维护

具体实现

• \(fa(x)\)表示节点\(x\)在树上的父亲
• \(dep(x)\)表示节点\(x\)在树上的深度
• \(siz(x)\)表示节点\(x\)的子树的节点个数
• \(son(x)\)表示节点\(x\)的重儿子
• \(top(x)\)表示节点\(x\)所在重链的顶部节点（深度最小）
• \(dfn(x)\)表示节点\(x\)的\(dfs\)序，也是其在线段树中的编号
• \(rnk(x)\)表示\(dfs\)序所对应的节点编号，有\(rnk(dfn(x))=x\)

我们进行两遍\(dfs\)预处理出这些值
第一次\(dfs\)求出\(fa(x)\),\(dep(x)\),\(siz(x)\),\(son(x)\)
第二次\(dfs\)求出\(top(x)\),\(dfn(x)\),\(rnk(x)\)

例题

【模板】重链剖分/树链剖分
https://www.luogu.com.cn/problem/P3384

#include <bits/stdc++.h>
using namespace std;
 
#define lson (rt << 1)
#define rson (rt << 1 | 1)
 
const int maxn = 1e5 + 10, maxm = 1e5 + 10;

//r:根节点  p:模数
int n = 0, m = 0, r = 0, p = 0;
int a[maxn] = {};
//邻接链表变量
int h[maxn] = {}, nxt[maxm<<1] = {}, to[maxm<<1] = {}, tot = 0;
//重链剖分变量
//fa(x) 表示节点 x 在树上的父亲
//dep(x) 表示节点 x 在树上的深度
//siz(x) 表示节点 x 的子树的节点个数
//son(x) 表示节点 x 的 重儿子
//top(x) 表示节点 x 所在 重链 的顶部节点（深度最小）
//dfn(x) 表示节点 x 的 DFS 序，也是其在线段树中的编号
//rnk(x) 表示 DFS 序所对应的节点编号，有 rnk(dfn(x))=x
//cnt 用来求dfs序
int fa[maxn] = {}, dep[maxn] = {}, siz[maxn] = {}, son[maxn] = {}, top[maxn] = {};
int dfn[maxn] = {}, rnk[maxn] = {}, cnt = 0;
//线段树变量
struct node
{
	int l, r, sum, lazy;
}tree[maxn<<2];

void pushup(int rt)
{
	tree[rt].sum = (tree[lson].sum + tree[rson].sum) % p;
}

//把当前节点rt的延迟标记下放到左右儿子
void pushdown(int rt)
{
	if(tree[rt].lazy)//此节点有延迟标记
	{
		int lz = tree[rt].lazy;
		tree[rt].lazy = 0;//记住要清零
		tree[lson].lazy = (tree[lson].lazy + lz) % p;
		tree[rson].lazy = (tree[rson].lazy + lz) % p;
		tree[lson].sum = (tree[lson].sum + lz * (tree[lson].r - tree[lson].l + 1) % p) % p;
		tree[rson].sum = (tree[rson].sum + lz * (tree[rson].r - tree[rson].l + 1) % p) % p;
	}
}

//建树
//l和r对应的是dfn
void Build(int rt, int l, int r)
{
	tree[rt].l = l;
	tree[rt].r = r;//节点信息初始化
	if(l == r)//到叶节点
	{
		//l为dfn值，所以rnk[l]对应的是原来的点
		tree[rt].sum = a[rnk[l]] % p;	
		return;
	}
	
	int mid = (l + r) >> 1;
	Build(lson, l, mid);
	Build(rson, mid+1, r);
	
	pushup(rt);//子树建好后，回溯时更新父节点信息
}

void Update(int rt, int l, int r, int val)
{
	//更新区间完全覆盖节点表示的区间
	if(l<=tree[rt].l && tree[rt].r<=r)
	{
		tree[rt].lazy = (tree[rt].lazy + val) % p;
		tree[rt].sum = (tree[rt].sum + val * (tree[rt].r - tree[rt].l + 1) % p) % p;
		return;
	}
	
	//如果不能完全覆盖，此时需要向下递归，要下放标记
	pushdown(rt);
	int mid = (tree[rt].l + tree[rt].r) >> 1;
	if(l <= mid) Update(lson, l, r, val);
	if(r > mid) Update(rson, l, r, val);
	
	pushup(rt);
}

//当前节点为rt,要查询的区间是[l, r]
int Query(int rt, int l, int r)
{
	int ret = 0;
	//如果节点表示的区间是查询区间的真子集
	if(l<=tree[rt].l && tree[rt].r<=r)
	{
		return tree[rt].sum % p;
	}
	
	//如果不能完全覆盖，此时需要向下递归，要下放标记
	pushdown(rt);
	int mid = (tree[rt].l + tree[rt].r) >> 1;
	if(l <= mid) ret = (ret + Query(lson, l, r)) % p;
	if(r > mid) ret = (ret + Query(rson, l, r)) % p;
	return ret;
}

void addedge(int x, int y)
{
	to[++tot] = y;
	nxt[tot] = h[x];
	h[x] = tot;
}

//求出 fa(x)，dep(x)，siz(x)，son(x)
void dfs1(int x)
{
	son[x] = -1;
	siz[x] = 1;
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		if(!dep[y])
		{
			dep[y] = dep[x] + 1;
			fa[y] = x;
			dfs1(y);
			siz[x] += siz[y];
			if(son[x]==-1 || siz[y]>siz[son[x]]) son[x] = y;
		}
	}
}

//求出 top(x)，dfn(x)，rnk(x)
void dfs2(int x, int t)
{
	top[x] = t;
	cnt++;
	dfn[x] = cnt;
	rnk[cnt] = x;
	if(son[x] == -1) return;	//x为叶子节点
	dfs2(son[x], t);// 优先对重儿子进行 DFS，可以保证同一条重链上的点 DFS 序连续
	for(int i=h[x]; i; i=nxt[i])
	{
		int y = to[i];
		//y为轻儿子时，单独开一条链，y为链顶端点
		if(y!=son[x] && y!=fa[x]) dfs2(y, y);	
	}
}

void add1(int x, int y, int val)
{
	//跳重链
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		Update(1, dfn[top[x]], dfn[x], val);
		x = fa[top[x]];
	}
	
	//已跳到同一条重链
	if(dep[x] > dep[y]) swap(x, y);
	Update(1, dfn[x], dfn[y], val);
}

int query1(int x, int y)
{
	int ret = 0;
	//跳重链
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		ret = (ret + Query(1, dfn[top[x]], dfn[x])) % p;
		x = fa[top[x]];
	}
	
	//已跳到同一条重链
	if(dep[x] > dep[y]) swap(x, y);
	ret = (ret + Query(1, dfn[x], dfn[y])) % p;
	return ret;
}

int main()
{   
	int op = 0, x = 0, y = 0, z = 0;
	scanf("%d%d%d%d", &n, &m, &r, &p);
	for(int i=1; i<=n; i++) scanf("%d", &a[i]);
	for(int i=1; i<n; i++)
	{
		scanf("%d%d", &x, &y);
		addedge(x, y);
		addedge(y, x);
	}

	//执行重链剖分,两遍 DFS 预处理出这些值，
	//第一次 DFS 求出 fa(x)，dep(x)，siz(x)，son(x) 
	dep[r] = 1;
	dfs1(r);
	//第二次 DFS 求出 top(x)，dfn(x)，rnk(x)。
	dfs2(r, r);

	//针对dfn序建树
	Build(1, 1, cnt);
	while(m--)
	{
		scanf("%d", &op);
		if(op == 1)
		{
			scanf("%d%d%d", &x, &y, &z);
			add1(x, y, z);
		}
		else if(op == 2)
		{
			scanf("%d%d", &x, &y);
			int ans = query1(x, y);
			printf("%d\n", ans);
		}
		else if(op == 3)
		{
			scanf("%d%d", &x, &z);
			Update(1, dfn[x], dfn[x]+siz[x]-1, z);
		}
		else if(op == 4)
		{
			scanf("%d", &x);
			int ans = Query(1, dfn[x], dfn[x]+siz[x]-1);
			printf("%d\n", ans);
		}
	}

	return 0;
}