嗣澳——扫,墨依奥——描,希伊桉——线
rt:
扫描线
定义
扫描线顾名思义就是用线扫描,维护区间的长度。它一般被用来解决图形面积,周长问题。
rt:

把整个矩形分成如图各个颜色不同的小矩形,小矩形的高是扫过的距离,然而矩形的水平宽一直在变化。
给每一个矩形的上下边进行标记,下面的边标记为 \(1\),上面的边标记为 \(-1\)。
每遇到一个水平边时,让这条边(在横轴投影区间)的权值加上这条边的标记。
小矩形(不一定只有一个)的宽度就是整个数轴上权值大于 \(0\) 的区间总长度。
实现
用线段树维护这根线。
维护两个值:
\(cnt\):整个区间被整体覆盖了几次(类似lazytag,但不下传)
\(len\):整个区间被覆盖的总长度
考虑修改
- 若遍历到一条下边,则对于这条下边的左右端点对应\(cnt\)在线段树上区间加一。
- 反之,若是一条
上巴上边,就区间\(cnt\)减一。
考虑\(pushup\)
- 若该区间\(cnt\)不为\(0\),则\(len\)值为对应区间的值。
*反之,则\(len\)值为左右子节点\(len\)值求和。
对于这条边对答案的贡献,直接取线段树根节点的\(len\)值。
其实是一个很抽象派意识流的东西,让我们看一下例题/板子理解一下。
例题(🚪)
洛谷 P5490 【模板】扫描线 & 矩形面积并
洛谷 P5490 【模板】扫描线 & 矩形面积并
嬷墨魔摩莫摸模膜末抹沫板

其矩形并集覆盖可以看成\(inf\)个规则的矩形拼起来,所以问题转化为\(inf\)个不交矩形的面积和。
由你的小学数学课本可知
让我们钦定横着的线是长,竖着的线是宽。
发现长可以用扫·神祇方法·计算几何·描线·线段树inf世来解决(高仿肝硬化),具体方法请 参上&&参见代码。
那么宽呢?
可以对横线以其纵坐标排序。
从小到大遍历,用线段树求出矩形的长。
然后通过与相邻的横线的纵坐标差相乘得到矩阵的面积,然后相加就是答案。
代码
#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1)
struct jade
{
int x1,x2,y;
int tag;
}line[200010];
struct seek
{
int l,r;
int cnt,len;
}t[200010<<3];
int X[200010];
bool cmp(jade x,jade y)
{
return x.y<y.y;
}
void build(int ro,int l,int r)
{
t[ro].l=l;
t[ro].r=r;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
void pushup(int ro)
{
int l=t[ro].l;
int r=t[ro].r;
if(t[ro].cnt)
{
t[ro].len=X[r+1]-X[l];
}
else
{
t[ro].len=t[ls].len+t[rs].len;
}
}
void change(int ro,int l,int r,int tag)
{
if(l<=t[ro].l&&t[ro].r<=r)
{
t[ro].cnt+=tag;
pushup(ro);
return ;
}
int mid=(t[ro].l+t[ro].r)>>1;
if(l<=mid)
{
change(ls,l,r,tag);
}
if(r>mid)
{
change(rs,l,r,tag);
}
pushup(ro);
return ;
}
int main()
{
int n,x1,x2,y1,y2;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x1>>y1>>x2>>y2;
line[i]={x1,x2,y1,1};
line[n+i]={x1,x2,y2,-1};
X[i]=x1;
X[n+i]=x2;
}
n*=2;
sort(line+1,line+1+n,cmp);
sort(X+1,X+1+n);
int tot=unique(X+1,X+1+n)-X-1;
build(1,1,tot-1);
long long ans=0;
for(int i=1;i<n;i++)
{
int l=lower_bound(X+1,X+1+tot,line[i].x1)-X;
int r=lower_bound(X+1,X+1+tot,line[i].x2)-X;
change(1,l,r-1,line[i].tag);
ans+=1ll*t[1].len*(line[i+1].y-line[i].y);
}
cout<<ans;
return 0;
}
洛谷 P1856 [IOI 1998 / USACO5.5] 矩形周长 Picture
洛谷 P1856 [IOI 1998 / USACO5.5] 矩形周长 Picture
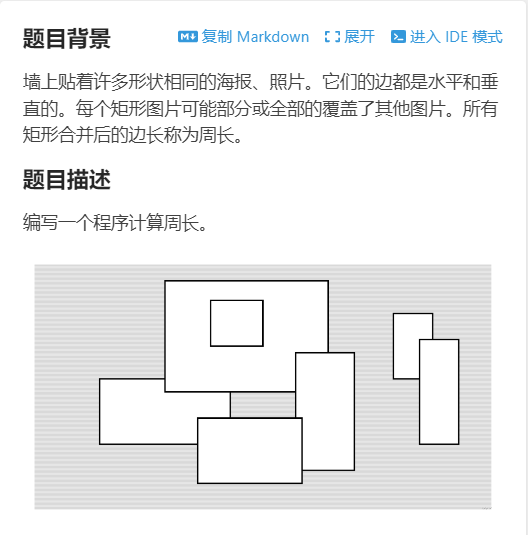
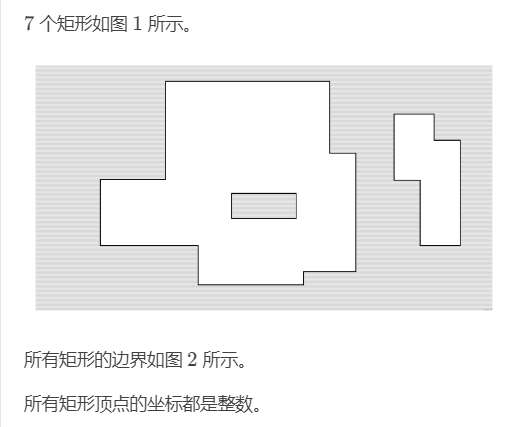
发现由求面积转化为了求边长,没关系,我们有小学数学课本啊!
以下提供两种解决方案:
解决方案 1 (by:僵尸)
考虑线段树维护三个值:
- 整个区间被几条互不相交的线段覆盖——\(num\)
- 另一个是整个区间被覆盖的总长度——\(len\)
- 再一个是整个区间被整体覆盖了几次——\(cnt\)
修改是一样的
考虑如何\(pushup\):
- 当其被一段横线覆盖时,即\(cnt\)不为\(0\):
\(len=r-l+1\),\(num=1\) - 当其是一个叶节点时:
\(len=0\),\(num=0\) - 当其既不也不时:
\(len\)为其左右儿子的\(len\)和
\(num\)为其左右儿子的\(num\)和
但发现一个问题,\(num\)的值是不对的,若它的左右儿子有一个共同端点(都被覆盖),就会有一个点被重复计算,所以要引入两个新的参数:\(lf\),\(rf\)(其区间的左右端点是否被覆盖),其跟随\(pushup\)更新即可。
考虑如何记录答案:
分别考虑长和宽。
长:这次线段树根节点的\(len\)值与上一次的\(len\)值作差
宽:这次线段树根节点的\(num\)值和相邻的横线的纵坐标差的乘积再乘上二(因为一个矩形有两个宽)
代码 1
#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1)
struct jade
{
int x1,x2,y,tag;
}line[10010];
struct seek
{
int l,r,cnt;
int len,num;
bool lf,rf;
}t[200010<<2];
bool cmp(jade x,jade y)
{
if(x.y==y.y)
{
return x.tag>y.tag;
}
return x.y<y.y;
}
void build(int ro,int l,int r)
{
t[ro].l=l;
t[ro].r=r;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
void pushup(int ro)
{
if(t[ro].cnt)
{
t[ro].len=t[ro].r-t[ro].l+1;
t[ro].lf=t[ro].rf=1;
t[ro].num=1;
}
else if(t[ro].l==t[ro].r)
{
t[ro].len=0;
t[ro].num=0;
t[ro].lf=t[ro].rf=0;
}
else
{
t[ro].len=t[ls].len+t[rs].len;
t[ro].lf=t[ls].lf;
t[ro].rf=t[rs].rf;
t[ro].num=t[ls].num+t[rs].num-(t[ls].rf&&t[rs].lf);
}
return ;
}
void change(int ro,int l,int r,int tag)
{
if(l<=t[ro].l&&t[ro].r<=r)
{
t[ro].cnt+=tag;
pushup(ro);
return ;
}
int mid=(t[ro].l+t[ro].r)>>1;
if(l<=mid)
{
change(ls,l,r,tag);
}
if(r>mid)
{
change(rs,l,r,tag);
}
pushup(ro);
return ;
}
int main()
{
int n;
cin>>n;
int maxl=INT_MAX;
int maxr=INT_MIN;
for(int i=1;i<=n;i++)
{
int x1,x2,y1,y2;
cin>>x1>>y1>>x2>>y2;
maxl=min(maxl,min(x1,x2));
maxr=max(maxr,max(x1,x2));
line[i]={x1,x2,y1,1};
line[i+n]={x1,x2,y2,-1};
}
n*=2;
sort(line+1,line+1+n,cmp);
long long ans=0,last=0;
build(1,maxl,maxr-1);
for(int i=1;i<=n;i++)
{
change(1,line[i].x1,line[i].x2-1,line[i].tag);
ans+=labs(t[1].len-last);
ans+=(line[i+1].y-line[i].y)*2*t[1].num;
last=t[1].len;
}
cout<<ans;
return 0;
}
解决方案 2 (by:肝硬化)
hiahiahiahiahia
发现其有长和宽两个值,所以开两个线段树分别维护横着扫一遍和竖着扫一遍的答案(及将竖着的宽转换为横线),再将答案相加。
代码 2
等等等等等等等等我管她要一下授权。
要啦QWQ
#include <bits/stdc++.h>
using namespace std;
#define lson (root << 1)
#define rson (root << 1 | 1)
const int _ = 5010;
int n, xa, xb, ya, yb, bfa, bfb;
long long ans;
struct rain{
int a[_ << 1], tot;
struct gyh{
int xa, xb, y, op;
inline bool operator < (const gyh & x)const{
return (y != x. y) ? (y < x. y) : op > x. op;
}
}xian[_ << 1];
struct hhh{
int l, r, v;
long long len;
}tree[_ << 3];
inline int zhao(int x){
return lower_bound(a + 1, a + tot + 1, x) - a;
}
inline void pushup(int root){
if(tree[root]. v){
tree[root]. len = a[tree[root]. r + 1] - a[tree[root]. l];
}
else if(tree[root]. l == tree[root]. r){
tree[root]. len = 0;
}
else{
tree[root]. len = tree[lson]. len + tree[rson]. len;
}
return ;
}
inline void build(int root, int l, int r){
tree[root] = {l, r, 0, 0};
if(l == r){
return ;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
return ;
}
inline void update(int root, int l, int r, int v){
if(tree[root]. l >= l && tree[root]. r <= r){
tree[root]. v += v;
pushup(root);
return ;
}
int mid = (tree[root]. l + tree[root]. r) >> 1;
if(l <= mid){
update(lson, l, r, v);
}
if(r > mid){
update(rson, l, r, v);
}
pushup(root);
return ;
}
}H, Z;
int main(){
scanf("%d", & n);
for(int i = 1; i <= n; i ++){
scanf("%d%d%d%d", & xa, & ya, & xb, & yb);
H. xian[i] = {xa, xb, ya, 1}, H. xian[i + n] = {xa, xb, yb, - 1};
Z. xian[i] = {ya, yb, xa, 1}, Z. xian[i + n] = {ya, yb, xb, - 1};
H. a[i] = xa, H. a[i + n] = xb;
Z. a[i] = ya, Z. a[i + n] = yb;
}
sort(H. a + 1, H. a + (n << 1 | 1));
sort(Z. a + 1, Z. a + (n << 1 | 1));
H. tot = unique(H. a + 1, H. a + (n << 1 | 1)) - H. a - 1;
Z. tot = unique(Z. a + 1, Z. a + (n << 1 | 1)) - Z. a - 1;
sort(H. xian + 1, H. xian + (n << 1 | 1));
sort(Z. xian + 1, Z. xian + (n << 1 | 1));
H. build(1, 1, H. tot - 1);
Z. build(1, 1, Z. tot - 1);
for(int i = 1; i <= (n << 1 | 1); i ++){
H. update(1, H. zhao(H. xian[i]. xa), H. zhao(H. xian[i]. xb) - 1, H. xian[i]. op);
Z. update(1, Z. zhao(Z. xian[i]. xa), Z. zhao(Z. xian[i]. xb) - 1, Z. xian[i]. op);
ans += (abs(H. tree[1]. len - bfa) + abs(Z. tree[1]. len - bfb));
bfa = H. tree[1]. len, bfb = Z. tree[1]. len;
}
printf("%lld", ans);
return 0;
}
POJ 2482 Stars in Your Window

转化转化转化
将星星\((x,y)\)看作一个矩形\((x,y),(x+w,y),(x,y+h-1),(x+w,y+h-1)\),然后跑扫描线,扫到每个矩形下边时将其对应的区间加上星星的亮度,扫到每个矩形上边时将其对应的区间减去星星的亮度。
具体的:将一个星星矩形的两个长边拿出来,按纵坐标排序,然后对于每次在线段树中加入一条长边后,都取一次根节点的\(cnt\)值,和之前的\(cnt\)值取\(max\),最大的就是答案。
因为每个星星矩形都有权值(亮度),所以每次修改时调用的不是\(+1,-1\),而是\(+权值,-权值\),同样的,也需要加入\(pushdown\)操作。
代码
#include<bits/stdc++.h>
using namespace std;
#define ls (ro<<1)
#define rs (ro<<1|1)
struct jade
{
int x1,x2,y,val;
}line[20010];
int X[20010];
bool cmp(jade x,jade y)
{
if(x.y==y.y)
{
return x.val<y.val;
}
return x.y<y.y;
}
struct seek
{
int l,r,cnt,lazy;
}t[10010<<3];
void build(int ro,int l,int r)
{
t[ro].l=l;
t[ro].r=r;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
return ;
}
void pushup(int ro)
{
t[ro].cnt=max(t[ls].cnt,t[rs].cnt);
return ;
}
void pushdown(int ro)
{
if(t[ro].lazy)
{
t[ls].lazy+=t[ro].lazy;
t[ls].cnt+=t[ro].lazy;
t[rs].lazy+=t[ro].lazy;
t[rs].cnt+=t[ro].lazy;
}
t[ro].lazy=0;
return ;
}
void add(int ro,int l,int r,int cnt)
{
if(l<=t[ro].l&&t[ro].r<=r)
{
t[ro].lazy+=cnt;
t[ro].cnt+=cnt;
return ;
}
pushdown(ro);
int mid=(t[ro].l+t[ro].r)>>1;
if(l<=mid)
{
add(ls,l,r,cnt);
}
if(r>mid)
{
add(rs,l,r,cnt);
}
pushup(ro);
return ;
}
int main()
{
int n,w,h;
while(cin>>n>>w>>h)
{
memset(t,0,sizeof(t));
memset(line,0,sizeof(line));
memset(X,0,sizeof(X));
int ans=0;
for(int i=1;i<=n;i++)
{
int x,y,val;
cin>>x>>y>>val;
line[i]={x,x+w,y,val};
line[i+n]={x,x+w,y+h-1,-val};
X[i]=x;
X[i+n]=x+w;
}
n*=2;
sort(X+1,X+1+n);
sort(line+1,line+1+n,cmp);
int tot=unique(X+1,X+1+n)-X-1;
build(1,1,tot-1);
for(int i=1;i<=tot;i++)
{
int l=lower_bound(X+1,X+1+tot,line[i].x1)-X;
int r=lower_bound(X+1,X+1+tot,line[i].x2)-X;
add(1,l,r-1,line[i].val);
ans=max(ans,t[1].cnt);
}
cout<<ans<<endl;
}
return 0;
}
总结(by:_dlwlrma)
以下引用自学长_dlwlrma link
用于计算若干个矩形的并的面积或周长及其延伸出来的问题。思想形象点来说大概就是将二维平面的某一维离散化后上线段树,然后按照一定顺序(一般是从小到大)扫描,同时维护树上信息(一般是当前区间内图形与扫描线交的长度)。
比普通线段树特殊的几点:
- 一般不需要特定的query函数,一般直接取根节点的值即可;
- 一般不需要下放标记,因为不会跳过一个父区间去访问一个子区间。但具体问题要具体对待。
- \(l\)一般代表\([l,l+1)\) 这个区间,所以某些地方的树上位置要相比实际位置-1。
推:肝硬化的扫描线精美博客link
也许 \({\cal {The }}\) \({\cal {end. }}\)
本文来自博客园,作者:BIxuan—玉寻,转载请注明原文链接:https://www.cnblogs.com/zhangyuxun100219/p/19150220



 浙公网安备 33010602011771号
浙公网安备 33010602011771号