扫描线
卸载前main:

废话
好像没有废话。
P








推歌
《人间白首》
提剑
斩我青丝一线
魂牵
你闯入我的世界
指上以血唤的焰
缠绕在剑边缘
饮一壶酒这人间
想斩开 天地
也不过一剑
在我身前
心 刹那停歇
此刻你在哪边
或许
七月初七 淮水竹亭
只是我一场泡影
或许
我的期待 我的梦境
没有结局
或许
经年以后 又是七夕
或许无我也无你
或许天各一方
不可葬一地
万般不会的事情
与你交付一颗心
眷恋的点点滴滴
踏剑于云晴时雨
你是人间的绝景
鞘中有剑笛不鸣
白首不负的心意
生生死死不可离弃
今生可否再遇
海誓山盟应许
如若将余世焚尽
而你的身影
失了一颗心
颤抖的手
有 万语千言
此刻你在眼前
或许
七月初七 淮水竹亭
只是我一场泡影
或许
我的期待 我的梦境
没有结局
或许
经年以后 又是七夕
或许无我也无你
或许天各一方
不可葬一地
无能为力的身影
血海深仇的命运
我所有心意难平
火点不燃一颗心
鞘里无剑 笛不发音
竹亭变作了院庭
情 生生死死 不可离弃
白首不相离
曾经
年少轻狂 无不可行
才知人终有穷尽
或许
天长地久 不是憧憬
半寸光阴
终究
我之中意 盖世无敌
上苍让我遇见你
或许此情绵绵
来生可再续
人间白首
葬笛与剑心
扫描线:
T1 Atlantis&【模板】扫描线 & 矩形面积并&[蓝桥杯 2017 省 A] 油漆面积
Solve:
扫描线,根据字面意思可以想到它的运行过程:一根线沿着一个方向扫描整个图,于是我们可以用它实现快速求矩形面积并的操作。
我们扫描由一堆矩形组成的一坨不知名物体(¿)时,不妨将这一坨不规则图形切成一摞规则的矩形,见下图(霍自OIwiki):
这不是咱的床单/被子吗【大雾】………
这样看起来就好求多了:原本有交的矩形们被砍成了许多无交的新矩形!于是就可以通过计算每个新矩形的面积,求和得出答案。由于扫描的是线段而不是矩形,于是我们可以直接存储线段,然后按照高度排序。当一个矩形下端的长被扫描到后,被扫描的部分增加,上端被扫描到则减少,于是可以用一个变量存储 \(1\) 标记同一个矩形较低的横线, \(−1\) 标记矩形较高的横线(这里默认从下往上扫,如果从上往下,那太唐了吧,反人类邪教邪教,我不这样写那么标记是相反的)。
如何计算切每个新矩形面积呢?我们需要知道矩形的底和高(可是我不知道)。矩形的高很好求,即为排序后相邻两横线间的距离。
想要维护矩形的底是不平凡的。每次扫到一根横线,我们要么将这根横线加入,要么将这根横线删除。
可以将一根横坐标在 \(l\)∼\(r\) 范围内的的横线拆成 \(l∼l+1,l+2∼l+3,…,r−1∼r\) 共 \(r−l\) 根长度为 \(1\) 的横线,对所有长度为 \(1\) 的横线都开一个桶来储存这根横线的数量。储存值大于 \(0\) 的桶的数量即为当前矩形的底,于是每加一根横线就将横线位置的值加一,减一根横线就将该位置减一。
这样我们可以发现这种操作可以使用线段树来维护,这里的线段树的每个节点都维护一段区间,我们需要维护区间的左端点、右端点、区间内横线数量,横线总长度(因为有相交的横线,我们不能将每个位置是否有横线平凡地设成零或一)。
于是,在向下递归节点时,如果当前节点被需要操作的区间完全覆盖,那么直接对横线的总长度进行修改;否则,就像平凡的线段树一样:如果操作区间和左儿子维护的区间相交,那么对左儿子递归,如果操作区间和右儿子维护的区间相交,那么对右儿子递归。
别忘了 \(pushup\) !!!(某人为此 \(inf~ms\) 白干)
于是你就可以 \(AC\) 板子题了。
ps:第一个自家 \(OJ\) 上的题注意多测清空;每组数据最后要输出两个换行(因为输出空行);开 \(double\) !!!
第三个数据过水理论 \(O(n^2)\) 可过(毕竟是黄题)。
Code:
这里给出自家OJ的神(逆)秘(天)代码
#include <bits/stdc++.h>
using namespace std;
#define lson (root << 1)
#define rson (root << 1 | 1)
const int _ = 10010;
int n, tot, num;
double a[_ << 1], xa, ya, xb, yb, ans;
struct rain{
double xa, xb, y;
int op;
}xian[_ << 1];
struct hhh{
int l, r, v;
double len;
}tree[_ << 3];
inline void pushup(int root){
if(tree[root]. v){
tree[root]. len = a[tree[root]. r + 1] - a[tree[root]. l];
}
else if(tree[root]. l == tree[root]. r){
tree[root]. len = 0;
}
else{
tree[root]. len = tree[lson]. len + tree[rson]. len;
}
return ;
}
inline void build(int root, int l, int r){
tree[root] = {l, r, 0, 0};
if(l == r){
return ;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
return ;
}
inline void update(int root, int l, int r, int v){
if(tree[root]. l >= l && tree[root]. r <= r){
tree[root]. v += v;
pushup(root);
return ;
}
int mid = (tree[root]. l + tree[root]. r) >> 1;
if(l <= mid){
update(lson, l, r, v);
}
if(r > mid){
update(rson, l, r, v);
}
pushup(root);
return ;
}
inline bool bbb(rain x, rain y){
return (x. y != y. y) ? x. y < y. y : x. op < y. op;
}
inline int zhao(double x){
return lower_bound(a + 1, a + tot + 1, x) - a;
}
int main(){
while(1){
scanf("%d", & n);
ans = 0;
if(! n){
return 0;
}
printf("Test case #%d\n", ++ num);
for(int i = 1; i <= n; i ++){
scanf("%lf%lf%lf%lf", & xa, & ya, & xb, & yb);
xian[i] = {xa, xb, ya, 1}, xian[i + n] = {xa, xb, yb, - 1};
a[i] = xa, a[i + n] = xb;
}
sort(a + 1, a + (n << 1 | 1));
tot = unique(a + 1, a + (n << 1 | 1)) - a - 1;
sort(xian + 1, xian + (n << 1 | 1), bbb);
build(1, 1, tot - 1);
update(1, zhao(xian[1]. xa), zhao(xian[1]. xb) - 1, xian[1]. op);
for(int i = 2; i <= (n << 1); i ++){
ans += (xian[i]. y - xian[i - 1]. y) * tree[1]. len;
update(1, zhao(xian[i]. xa), zhao(xian[i]. xb) - 1, xian[i]. op);
}
printf("Total explored area: %.2lf\n\n", ans);
}
return 0;
}
T2 [IOI1998] [USACO5.5] 矩形周长Picture
Solve:
IAKIOI!
看到题面,非常开心——怎么比 \(T1\) 还水?于是开开心心结构体暴力封装线段树,左右扫了一遍,上下扫了一遍,每次更新后答案直接无脑加,企图萌混过关,然后, \(CH_4\) 了。
于是我们可以发现这样的一坨:
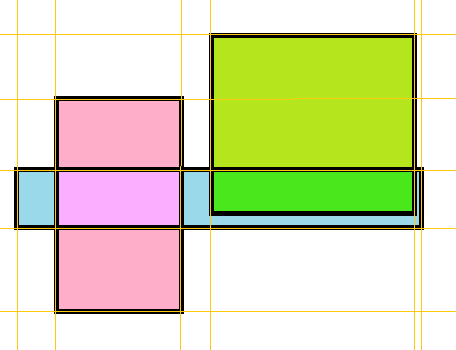
黄线是我们扫到的答案:
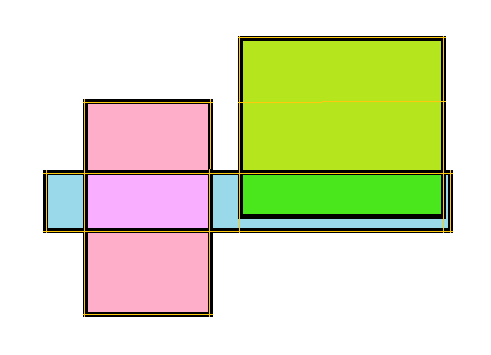
很显然,我们每次增加的周长长度是该次找到的线段长度减去上一次的。
于是没了,左右上下两棵树,扔掉脑子做自己!
其实跑得很快,而且码量很小,用学姐的码风压完行只有六十多行………
Code:
放心看没压行只是调用的有点怪
#include <bits/stdc++.h>
using namespace std;
#define lson (root << 1)
#define rson (root << 1 | 1)
const int _ = 5010;
int n, xa, xb, ya, yb, bfa, bfb;
long long ans;
struct rain{
int a[_ << 1], tot;
struct gyh{
int xa, xb, y, op;
inline bool operator < (const gyh & x)const{
return (y != x. y) ? (y < x. y) : op > x. op;
}
}xian[_ << 1];
struct hhh{
int l, r, v;
long long len;
}tree[_ << 3];
inline int zhao(int x){
return lower_bound(a + 1, a + tot + 1, x) - a;
}
inline void pushup(int root){
if(tree[root]. v){
tree[root]. len = a[tree[root]. r + 1] - a[tree[root]. l];
}
else if(tree[root]. l == tree[root]. r){
tree[root]. len = 0;
}
else{
tree[root]. len = tree[lson]. len + tree[rson]. len;
}
return ;
}
inline void build(int root, int l, int r){
tree[root] = {l, r, 0, 0};
if(l == r){
return ;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
return ;
}
inline void update(int root, int l, int r, int v){
if(tree[root]. l >= l && tree[root]. r <= r){
tree[root]. v += v;
pushup(root);
return ;
}
int mid = (tree[root]. l + tree[root]. r) >> 1;
if(l <= mid){
update(lson, l, r, v);
}
if(r > mid){
update(rson, l, r, v);
}
pushup(root);
return ;
}
}H, Z;
int main(){
scanf("%d", & n);
for(int i = 1; i <= n; i ++){
scanf("%d%d%d%d", & xa, & ya, & xb, & yb);
H. xian[i] = {xa, xb, ya, 1}, H. xian[i + n] = {xa, xb, yb, - 1};
Z. xian[i] = {ya, yb, xa, 1}, Z. xian[i + n] = {ya, yb, xb, - 1};
H. a[i] = xa, H. a[i + n] = xb;
Z. a[i] = ya, Z. a[i + n] = yb;
}
sort(H. a + 1, H. a + (n << 1 | 1));
sort(Z. a + 1, Z. a + (n << 1 | 1));
H. tot = unique(H. a + 1, H. a + (n << 1 | 1)) - H. a - 1;
Z. tot = unique(Z. a + 1, Z. a + (n << 1 | 1)) - Z. a - 1;
sort(H. xian + 1, H. xian + (n << 1 | 1));
sort(Z. xian + 1, Z. xian + (n << 1 | 1));
H. build(1, 1, H. tot - 1);
Z. build(1, 1, Z. tot - 1);
for(int i = 1; i <= (n << 1 | 1); i ++){
H. update(1, H. zhao(H. xian[i]. xa), H. zhao(H. xian[i]. xb) - 1, H. xian[i]. op);
Z. update(1, Z. zhao(Z. xian[i]. xa), Z. zhao(Z. xian[i]. xb) - 1, Z. xian[i]. op);
ans += (abs(H. tree[1]. len - bfa) + abs(Z. tree[1]. len - bfb));
bfa = H. tree[1]. len, bfb = Z. tree[1]. len;
}
printf("%lld", ans);
return 0;
}
T3 窗口的星星
Solve:
很明显我们不会。
我们考虑怎么把它变成形似扫描线板子的东西,我们可以发现窗户的大小一定,于是可以用窗户的右上角坐标代替窗户,对于每颗星星,我们考虑窗户的右上角在哪个位置可以使它被窗户框住:
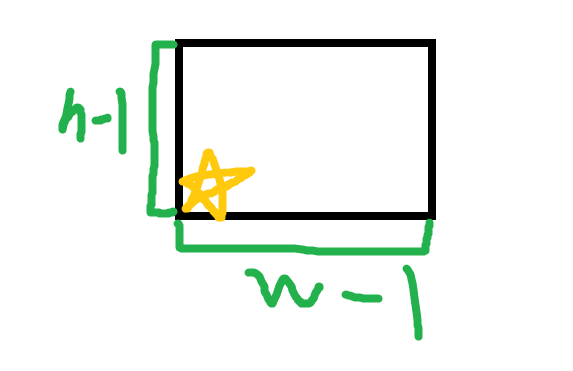
rt,当窗户长为 \(w\) ,高为 \(h\) 时,右上角可能在这个矩形中。
于是我们预处理出每个矩形,然后求最大的交即可。
注意:此时因为星星是有亮度权值的,于是我们的 \(0/-1\) 要改成 \(c/-c\) (亮度值)。此时这是一个更加不平凡的东西,我们的 \(pushdown\) 就不得不不省略了。
Code:
有史慎入!!!
#include <bits/stdc++.h>
using namespace std;
#define int long long//不开龙龙见奶龙!
#define lson (root << 1)
#define rson (root << 1 | 1)
const int _ = 10010;
int t, n, w, h, a[_ << 1], tot, ans, x, y, c;
namespace gua{
struct rain{
int xa, xb, y, c;
inline bool operator < (const rain & x)const{
return (y != x. y) ? (y < x. y) : c < x. c;
}
}astar[_ << 1];
inline int zhao(int x){
return lower_bound(a + 1, a + tot + 1, x) - a;
}
}
struct miaomiaomiao{
struct hhh{
int l, r, v, lazy;
}tree[_ << 3];
inline void pushup(int root){
tree[root]. v = max(tree[lson]. v, tree[rson]. v);
return ;
}
inline void pushdown(int root){
if(tree[root]. lazy){
tree[lson]. lazy += tree[root]. lazy;
tree[lson]. v += tree[root]. lazy;
tree[rson]. lazy += tree[root]. lazy;
tree[rson]. v += tree[root]. lazy;
}
tree[root]. lazy = 0;
return ;
}
inline void build(int root, int l, int r){
tree[root] = {l, r, 0, 0};
if(l == r){
return ;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
return ;
}
inline void update(int root, int l, int r, int v){
if(tree[root]. l >= l && tree[root]. r <= r){
tree[root]. lazy += v;
tree[root]. v += v;
return ;
}
pushdown(root);
int mid = (tree[root]. l + tree[root]. r) >> 1;
if(l <= mid){
update(lson, l, r, v);
}
if(r > mid){
update(rson, l, r, v);
}
pushup(root);
return ;
}
}H;
signed main(){
scanf("%lld", & t);
woshinailong :
if(scanf("%lld%lld%lld", & n, & w, & h) != EOF){
ans = 0;
for(int i = 1; i <= n; i ++){
scanf("%lld%lld%lld", & x, & y, & c);
gua :: astar[i] = {x, x + w, y, c}, gua :: astar[i + n] = {x, x + w, y + h, - c};
a[i] = x, a[i + n] = x + w;
}
sort(a + 1, a + (n << 1 | 1));
tot = unique(a + 1, a + (n << 1 | 1)) - a - 1;
sort(gua :: astar + 1, gua::astar + (n << 1 | 1));
H. build(1, 1, tot - 1);
for(int i = 1; i <= (n << 1); i ++){
H. update(1, gua :: zhao(gua :: astar[i]. xa), gua :: zhao(gua :: astar[i]. xb) - 1, gua :: astar[i]. c);
ans = max(ans, H. tree[1]. v);
}
printf("%lld\n", ans);
goto woshinailong;
}
return 0;
}
T4 【模板】离线二维数点
Solve:
这其实是肝硬化自己加的qwq。(因为它的题目背景有青蛙)
对于一个一个 \([l,r]\) 的答案,可以想到用 \([1,r]\) 的答案减去 \([1,l−1]\) 的答案,于是可以直接变为两段计算。考虑对每个 \([1,i]\) 计算答案,我们将询问和输入的序列排序后发现可以直接 \(1∼n\) 加点,因为要维护 \([1,i]\) 中存在多少个 \(≤x\) 的元素,于是可以直接使用权值树状数组(毕竟码量比线段树少很多,而且很好看),由于数据范围很小甚至不需要离散化,最终可以做到复杂度 \(O(nlogn)\) ,非常简单也是。
Code:
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & - x)
const int _ = 2000010;
int n, m, l, r, x, tree[_], ans[_], nw = 1;
struct hhh{
int l, r, v, num;
}q[_];
struct hh{
int v, num;
}a[_];
inline bool bbb(hh x, hh y){
return x. v < y. v;
}
inline bool ccc(hhh x, hhh y){
return x. v < y. v;
}
inline void add(int x, int v){
for(; x <= n; x += lowbit(x)){
tree[x] += v;
}
return ;
}
inline int query(int l, int r){
int as = 0;
for(; r; r -= lowbit(r)){
as += tree[r];
}
for(; l; l -= lowbit(l)){
as -= tree[l];
}
return as;
}
int main(){
scanf("%d%d", & n, & m);
for(int i = 1; i <= n; i ++){
scanf("%d", & a[i]. v);
a[i]. num = i;
}
for(int i = 1; i <= m; i ++){
scanf("%d%d%d", & q[i]. l, & q[i]. r, & q[i]. v);
q[i]. num = i;
}
sort(a + 1, a + n + 1, bbb);
sort(q + 1, q + m + 1, ccc);
for(int i = 1; i <= m; i ++){
while(nw <= n && a[nw]. v <= q[i]. v){
add(a[nw]. num, 1);
nw ++;
}
ans[q[i]. num] = query(q[i]. l - 1, q[i]. r);
}
for(int i = 1; i <= m; i ++){
printf("%d\n", ans[i]);
}
return 0;
}
T5 [SHOI2007] 园丁的烦恼
Solve:
这题数据好水线段树数组瞎开都能过。
注意:坐标范围很大,需要离散化;如果你神秘 \(RE~~or~~WA\) ,可能是离散化数组开小了,应该开到六倍; \(lower\)_\(bound\) 不要瞎复制粘贴,记得改变量名不然又白干半小时;坐标从 \(0\) 开始,但是线段树从零开始会炸得很彻底,应加一。
然后几乎是板子,后天会再粘一个图解释。
Code:
#include <bits/stdc++.h>
using namespace std;
#define lson (root << 1)
#define rson (root << 1 | 1)
int n, m, xa, xb, ya, yb, x, y, tot, ans[500010], a[3000010], nw;
struct gyh{
int x, y;
}shu[500010];
struct rain{
int xa, xb, ya, yb, num;
}cun[500010];
inline bool aaa(gyh x, gyh y){
return x. x < y. x;
}
inline bool bbb(rain x, rain y){
return x. xa < y. xa;
}
inline bool ccc(rain x, rain y){
return x. xb < y. xb;
}
struct hhh{
int l, r, v;
}tree[6000010];
inline void pushup(int root){
if(tree[root]. l == tree[root]. r){
return ;
}
tree[root]. v = tree[lson]. v + tree[rson]. v;
return ;
}
inline void build(int root, int l, int r){
tree[root] = {l, r, 0};
if(l == r){
return ;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
return ;
}
inline void update(int root, int p){
if(tree[root]. l == tree[root]. r){
if(tree[root]. l == p){
tree[root]. v ++;
}
return ;
}
int mid = (tree[root]. l + tree[root]. r) >> 1;
if(p <= mid){
update(lson, p);
}
else{
update(rson, p);
}
pushup(root);
return ;
}
inline int query(int root, int l, int r){
if(tree[root]. l >= l && tree[root]. r <= r){
return tree[root]. v;
}
int mid = (tree[root]. l + tree[root]. r) >> 1, as = 0;
if(l <= mid){
as += query(lson, l, r);
}
if(r > mid){
as += query(rson, l, r);
}
return as;
}
int main(){
scanf("%d%d", & n, & m);
for(int i = 1; i <= n; i ++){
scanf("%d%d", & x, & y);
x ++, y ++;
shu[i] = {x, y};
a[++ tot] = x, a[++ tot] = y;
}
for(int i = 1; i <= m; i ++){
scanf("%d%d%d%d", & xa, & ya, & xb, & yb);
xa ++, xb ++, ya ++, yb ++;
cun[i] = {xa, xb, ya, yb, i};
a[++ tot] = xa, a[++ tot] = xb, a[++ tot] = ya, a[++ tot] = yb;
}
sort(a + 1, a + tot + 1);
tot = unique(a + 1, a + tot + 1) - a - 1;
for(int i = 1; i <= n; i ++){
shu[i]. x = lower_bound(a + 1, a + tot + 1, shu[i]. x) - a;
shu[i]. y = lower_bound(a + 1, a + tot + 1, shu[i]. y) - a;
}
for(int i = 1; i <= m; i ++){
cun[i]. xa = lower_bound(a + 1, a + tot + 1, cun[i]. xa) - a;
cun[i]. xb = lower_bound(a + 1, a + tot + 1, cun[i]. xb) - a;
cun[i]. ya = lower_bound(a + 1, a + tot + 1, cun[i]. ya) - a;
cun[i]. yb = lower_bound(a + 1, a + tot + 1, cun[i]. yb) - a;
}
sort(shu + 1, shu + n + 1, aaa);
sort(cun + 1, cun + m + 1, bbb);
build(1, 1, 2000000);
for(int i = 1; i <= m; i ++){
while(nw <= n && cun[i]. xa > shu[nw + 1]. x){
nw ++;
update(1, shu[nw]. y);
}
ans[cun[i]. num] -= query(1, cun[i]. ya, cun[i]. yb);
}
build(1, 1, 2000000);
sort(cun + 1, cun + m + 1, ccc);
nw = 0;
for(int i = 1; i <= m; i ++){
while(cun[i]. xb >= shu[nw + 1]. x && nw <= n){
nw ++;
update(1, shu[nw]. y);
}
ans[cun[i]. num] += query(1, cun[i]. ya, cun[i]. yb);
}
for(int i = 1; i <= m; i ++){
printf("%d\n", ans[i]);
}
return 0;
}
END.
本文来自博客园,作者:养鸡大户肝硬化,转载请注明原文链接:https://www.cnblogs.com/rain20100708/p/19151517

 斯奥·魔伊拗·溪黯!
斯奥·魔伊拗·溪黯!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号