KL散度的无偏估计

http://joschu.net/blog/kl-approx.html

KL散度定义为:
\(KL[p,q]=\sum_x q(x)log \frac{q(x)}{p(x)}=E_{x\sim q}[log \frac{q(x)}{p(x)}]\)
这个博客证明了为什么这个值可以用$ \frac{1}{2} (\log p(x)-\log q(x))^2$ , x from q分布来估计.

一个统计量好的估计是无偏的(均值是对的)并且 具有低方差.
这里面定义\(r=\frac{p(x)}{q(x)}, k_1=\log \frac{q(x)}{p(x)}=-\log r\)
\(k_2= \frac{1}{2} (\log r )^2\)

\(k_1\)具有高的方差,因为他的值有一半是负的.因为KL散度永远是正的. 因为两个概率分布,p(x)和q(x)比值是否大于1,基本是接近0.5概率的.所以一半是负的. log1=0

\(k_1这个公式再加一个期望为0的就能降低方差,并且保持无偏,我们 p(x)/q(x)期望是1\),所以我们有下面公式其中
第二个.在原始的k1前面加了一个(r-1)即可.

最后的最好的公式是这个:

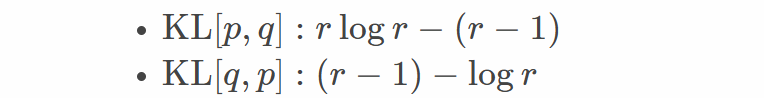
测试代码:

import torch.distributions as dis
p = dis.Normal(loc=0, scale=1)
q = dis.Normal(loc=0.1, scale=1)
x = q.sample(sample_shape=(10_000_000,))
truekl = dis.kl_divergence(p, q) # 这个是理论值, 也就是拿到p,q的解析式的分布进行计算kl散度.
print("true", truekl)
logr = p.log_prob(x) - q.log_prob(x)
L=0.999
k1 = -logr
k2 = logr ** 2 / 2
k3 = (logr.exp() - 1) - logr
k4=  L*(logr.exp() - 1) - logr
for k in (k1, k2, k3,k4):
    print((k.mean() - truekl) / truekl, k.std() / truekl) # 计算相对的均值误差, 以及标准差误差. 可以看到k3的值均值和误差都比k1,k2要小很多.