论文解读-《Dynamic Triangulation-Based Graph Rewiring for Graph Neural Networks》
1. 论文介绍
论文题目:Dynamic Triangulation-Based Graph Rewiring for Graph Neural Networks
论文领域:图神经网络,图重连算法,图三角测量
论文发表: CIKM 2025
论文核心算法(关键词): TRIGON
论文地址: https://arxiv.org/abs/2508.19071
论文代码:https://github.com/Hugo-Attali/TRIGON-CIKM-2025
论文背景:

2. 论文摘要
图神经网络 (GNN) 已成为学习图结构数据的主要范式。然而,它们的性能受到图拓扑固有问题的限制,最明显的是过度压缩和过度平滑。图重连的最新进展旨在通过修改图拓扑来促进更有效的信息传播来减轻这些限制。在这项工作中,我们介绍了 TRIGON,这是一个新颖的框架,它通过学习从多个图视图中选择相关三角形来构建丰富的非平面三角剖分。通过共同优化三角形选择和下游分类性能,与现有的重布线方法相比,该方法生成的结构特性显着改善,例如直径减小、谱间隙增加和有效电阻降低。实证结果表明,TRIGON 在一系列同性恋和异性恋基准的节点分类任务上优于最先进的方法。
3. 相关介绍
3.1 消息传递模式的局限性
消息传递的严格局部性质可能不太适合现实世界的结构,这种限制在低同质图(相邻节点倾向于属于不同的类)中变得尤为突出。局部邻域内的特征分布通常表现出较高的类间方差,违反了标准消息传递方案利用的局部同质性的基本假设。
3.2 德劳内三角(Delaunay triangulation)
传统用于表面网格划分和点云分析,通过最大化每一个三角形的最小角度来生成条件良好的网络,以应用图重连算法。
特征空间中的德劳内三角测量无法捕获对于有效下游分类可能至关重要的非局部或高阶结构。
Delaunay重连算法引入了结构良好的局部连接,已被证明可以减少过度挤压和过度平滑等现象,但本质上将图重连算法的限制在空间上近端节点,这种约束忽视了非局部三角形的潜在贡献,非局部三角形可以在增强全局信息流和改善远程消息传播方面发挥了关键作用。
3.3 论文贡献
- 基于三角形的图重连算法的理论分析,使用不同的方式分析三角形对图结构的影响和及对消息传递的影响。
- 用于图重连的可微三角形的选择。提出了TRIGON算法,一个可学习的模块,根据三角形和分类目标的相关性对三角形进行评分和选择。
- 综合的实验的验证。证明了我们的可学习重连方法优于基于静态的德劳内和其他最先进的图重连算法
4. TRIGON算法
4.1 基于三角形感知的图重连
图神经网络基于消息传递框架,其中节点表示通过局部交互迭代细化,在每一层,节点通常使用排列不变函数聚合来自其直接邻居的消息,然后通过可学习映射进行转换。
基于三角形的基序来重新连接图拓扑,从而改善信息传播的途径。三角形不仅编码了强大的局部凝聚力,还促进了全局的连通性。边(i,j) 的有效阻力允许上限为
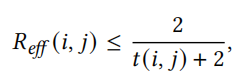
其中t(i,j) 表示包含边(i, j)的三角形的数量。这种反比关系表明嵌入许多三角形中的边支持阻力通信路径。
Delaunay重连线算法,证明了基于三角形的图重连算法是有用的,通过保持边缘曲率接近于零,有助于减轻过度平滑和过度挤压。
4.2 使用TRIGON进行可微分图重连
TRIGON,一种以三角形选择为中心的可学习的图重连算法,不依赖于固定的连通性规则,在训练过程中通过识别支持判别学习和稳健信息流的三角形来适应构造图。
TRIGON算法的整体架构
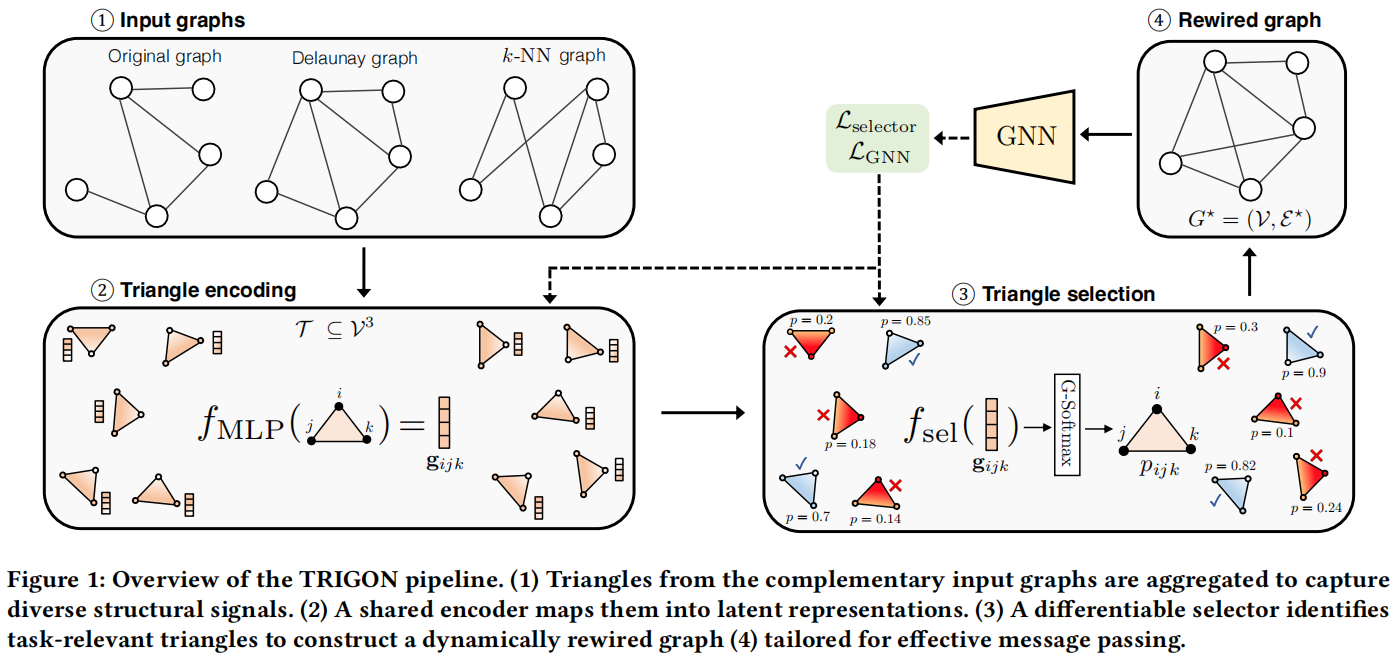
4.3 三角形编码
对于每个三角形(i, j, k),通过串联构造一个原始特征表示 $z_{ijk} =|x_i||x_j||x_k| \in R^{3d}$ ,表示由三角形编码器网络处理,厨卫多层感知机MLP来实现
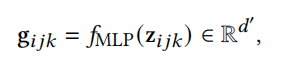
生成的该嵌入$g_{ijk}$,既捕捉了三角形顶点之间的几何关系,也体现了基于特征的关系。
4.4 可微三角形选择
为了确定哪些三角形对新的图结构有贡献,可以将g通过另一个MLP来传递嵌入
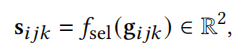
该MLP输出二进制选择的日志,使用 $\tau > 0$ 的Gumbel-softmax可以获得离散选择的可微近似值。
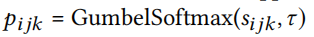
其中pijk是在最终连接的图中选择三角形(i,j,k)的概率。
这种松弛通过使用连续的,可微分的替代物近似分类抽样,好处是促进通过其他离散选择过程的梯度流动,可以有效地学习优先考虑对下游任务贡献最大的三角形,同时保持与基于梯度的优化完全兼容。
4.5 图重建
从选定的三角形集合中
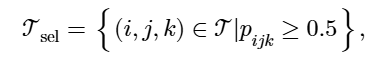
将边集重建为每个三角形引起的边的并集
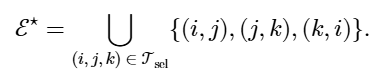
重新连接的图聚合了局部和非局部的三角形,形成具有增强扩展特性的非平面结构。
4.6 训练的损失函数
为了共同优化三角形选择和下游节点分类,定义了一个多分量损失函数。损失函数整合了四个互补的组成部分:
1) 监督分类损失: 就是节点预测类概率i和基本标签的差异,采用平均交叉熵。
2) 对比三角形标签损失:
为了引导三角形选择器 $f_{sel}$ 朝向具有信息性的类层,为每个三角形定义了一个二元监督信号
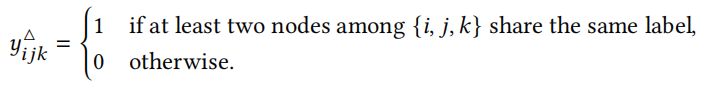
使用对比损失函数
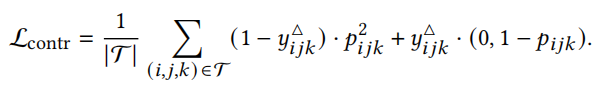
3) 结构光滑度损失
引入了一种结构正则化器,鼓励选择几何相干的三角形

4) 基于类的参与正规化
定义了一个正则化项,该项强制执行共享同一类的节点之间三角形参与的一致性。
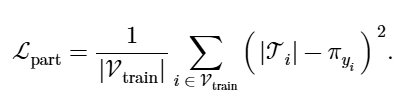
5) 聚合损失和联合训练
首先,通过最小化复合损失来优化三角形选择
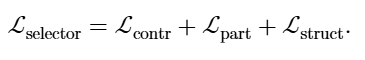
然后,使用该图来训练具有标准监督目标的 GNN。
每次迭代在这两个步骤之间交替,逐渐完善拓扑和节点表示。
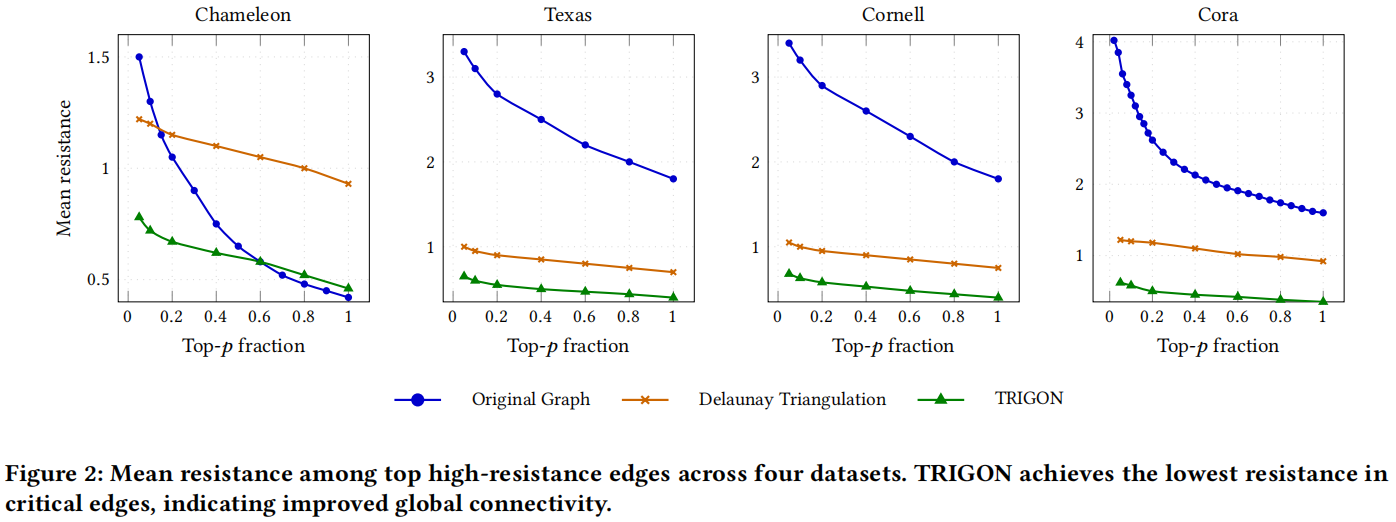
4.7 TRIGON图重连后的图结构特征分析
与原始图和 Delaunay 重连算法相比,TRIGON 重连的图在最高电阻分位数中始终表现出较低的平均有效电阻。这种减少对于对应于最关键边缘的 p 低值尤为明显,这表明 TRIGON 有助于缓解此类结构瓶颈。
平均电阻的比较
图直径和谱图间隙的比较
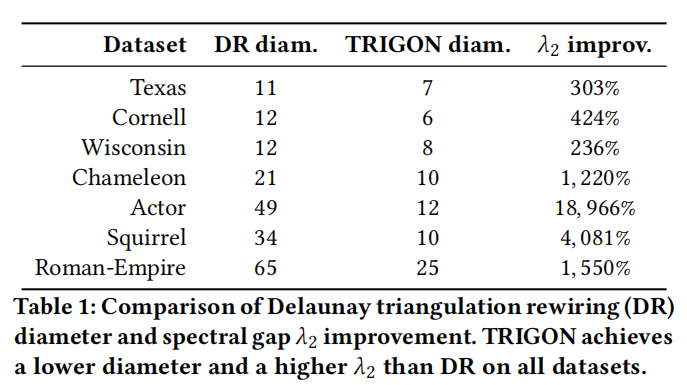
5. 实验设置
5.1 基础实验
数据集选择:
针对节点分类问题,选择十个数据集,三个同质数据集,七个异质数据集
基线模型:
将TRIGON和其他八种算法进行比较,FA,DIGL,SDRF,FOSR,BORF,GTR,DR, JDR。
实验超参数的调节和设置需要看原论文,提供了详细的调参方案。
实验结果
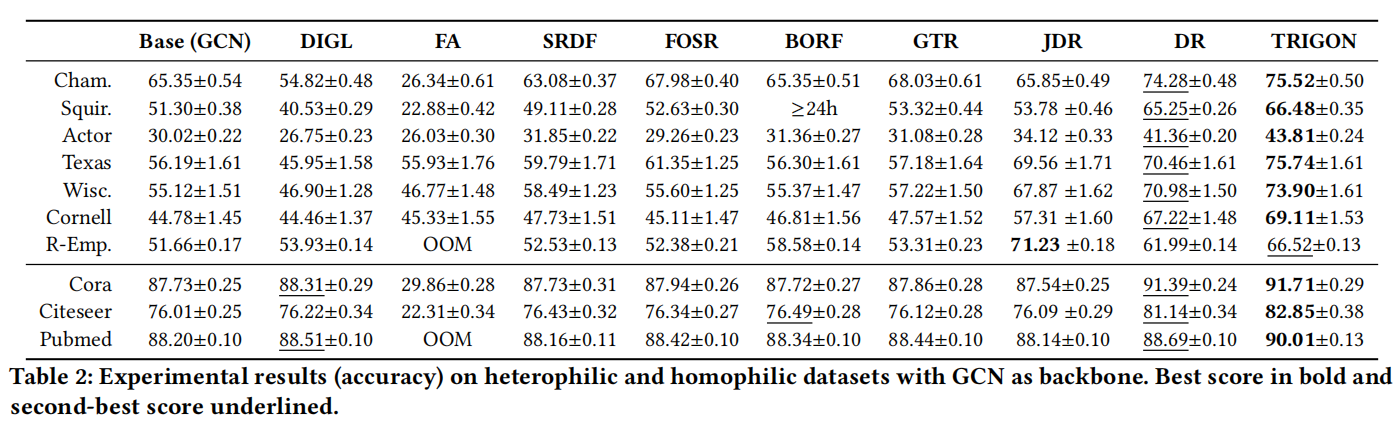
TRIGON 在十分之九的评估基准中优于最先进的图重新布线技术,无论主干网(GCN 或 GAT)如何,在同质和异质数据集条件下。
5.2 过度平滑分析
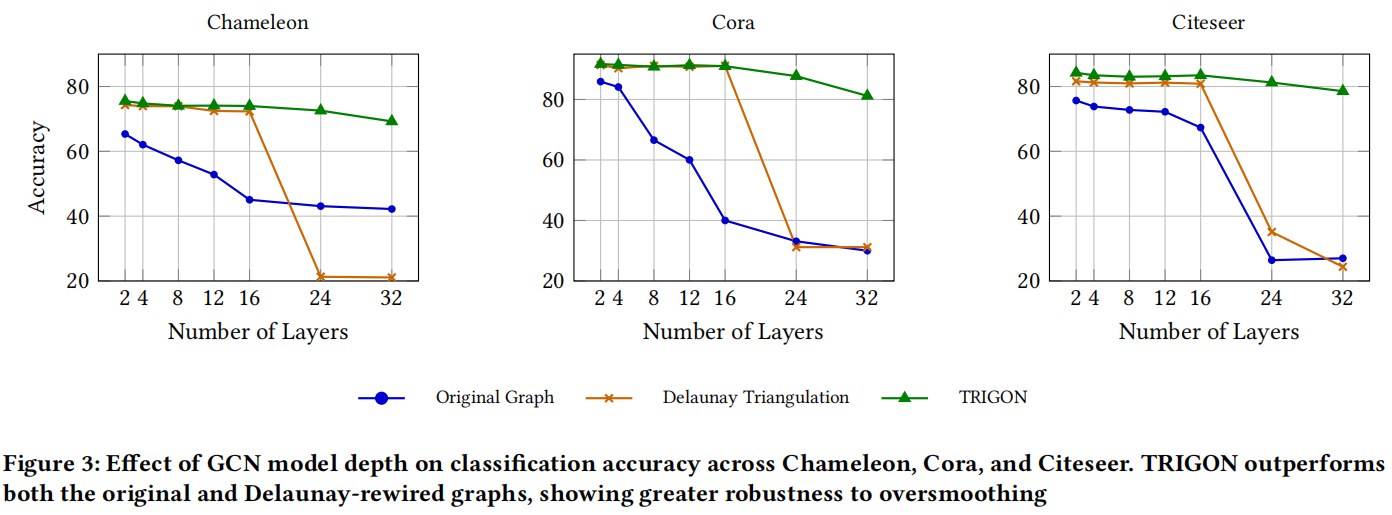
随着深度的增加,标准 GCN 的性能急剧下降,证实了过度平滑的存在。基于 Delaunay 的重新布线 (DR) 提供了改进,但仍然会在几层之外出现退化。相比之下,我们的方法 (TRIGON) 在所有深度上始终产生更高的准确性,表明更强地保留了表征多样性。这些发现表明,任务感知的非局部三角形选择可以有效地延迟或减轻过度平滑,同时还可以改善全局连通性和信息传播。
5.3 消融实验
消融实验来评估三角形选择机制的贡献以及 TRIGON 的相关损失分量。此外,我们还评估了候选三角形源、原始图和 k -NN 图的影响,以量化整合结构和基于特征的信息的好处。
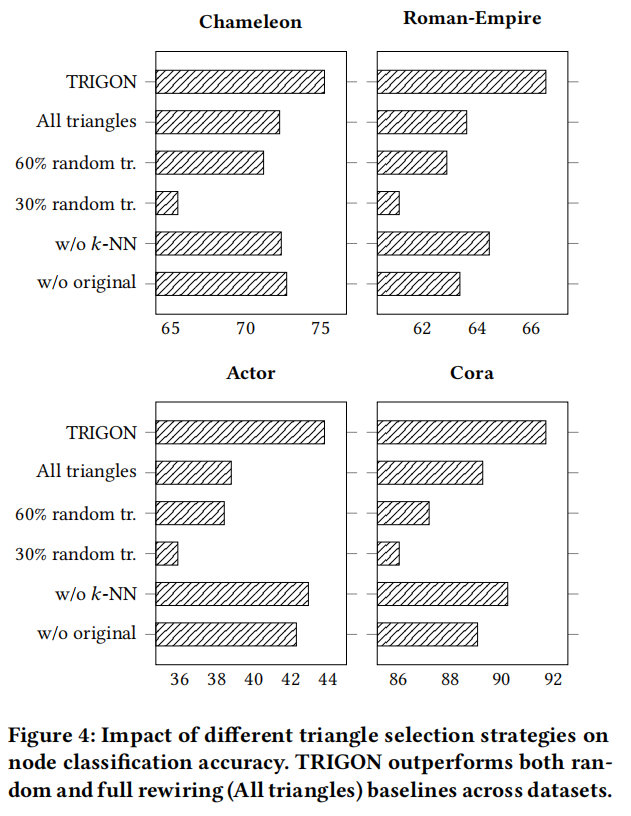
随着更多三角形的添加,性能逐渐提高,这表明增加的连通性通常有利于分类任务。值得注意的是,我们提出的选择策略始终取得最佳结果,表明绩效提升不仅源于三角形的数量,还源于所选三角形的相关性和有效性。此外,从原始图或 k -NN 图中消融三角形会导致所有数据集的性能下降。这凸显了保留原始拓扑结构先验和基于特征的邻近关系的重要性,它们共同提供了有效重新布线所必需的补充信息。

将每个损失项单独从训练目标中移除的影响。这些结果表明,损失函数的三个组成部分都是引导选择实现结构连贯且任务相关重接的必要条件。这表明监督在塑造支持有效消息传递的重构拓扑中起着重要作用。
6. 核心代码
构造三角形的选择器
# === Triangle Selector ===
class TriangleSelector(nn.Module):
def __init__(self, input_dim,num_classes):
super().__init__()
self.fc1 = nn.Linear(input_dim, 64)
self.bn1 = nn.BatchNorm1d(64)
self.fc3 = nn.Linear(64, 32)
self.bn3 = nn.BatchNorm1d(32)
self.fc4 = nn.Linear(32, 16)
self.bn4 = nn.BatchNorm1d(16)
self.fc5 = nn.Linear(16, 2)
self.dropout = nn.Dropout(0.5)
self.tau = nn.Parameter(torch.tensor(1.0))
self.pi = nn.Parameter(torch.arange(1, num_classes + 1, device=device, dtype=torch.float32) * 6)
def forward(self, x):
x = F.relu(self.bn1(self.fc1(x)))
x = self.dropout(x)
x = F.relu(self.bn3(self.fc3(x)))
x = self.dropout(x)
x = F.relu(self.bn4(self.fc4(x)))
x = self.dropout(x)
logits = self.fc5(x)
tau = F.softplus(self.tau)
probs = F.gumbel_softmax(logits, tau=tau, hard=True)
return probs[:, 1], tau
def triangle_participation_loss(self, selected_triangles, node_labels, train_mask):
triangle_counts = torch.zeros_like(node_labels, dtype=torch.float, device=node_labels.device)
for i, j, k in selected_triangles:
if train_mask[i] and train_mask[j] and train_mask[k]:
triangle_counts[i] += 1
triangle_counts[j] += 1
triangle_counts[k] += 1
targets = self.pi[node_labels]
mask = train_mask
return F.mse_loss(triangle_counts[mask], targets[mask])
联合训练核心过程
for epoch in range(1000):
triangle_features_transformed = triangle_mlp(features)
#
preds, tau = triangle_selector(triangle_features_transformed)
loss_mlp = contrastive_loss(preds, triangle_labels)
selected = preds > 0.5
selected_triangles = [tri for tri, keep in zip(triangles, selected.cpu()) if keep.item()]
with torch.no_grad():
_, x2 = gcn(node_features, edge_index_original)
loss_struct = structural_loss(selected_triangles, x2, train_mask)
loss_participation = triangle_selector.triangle_participation_loss(selected_triangles, labels, train_mask)
total_loss = loss_mlp + loss_participation + loss_struct
total_loss.backward()
opt_mlp.step()
opt_sel.step()
# Rebuild edge_index
edge_set = set()
for i, j, k in selected_triangles:
edge_set.update([(i, j), (j, k), (k, i)])
edge_index_final = torch.tensor(list(edge_set), dtype=torch.long, device=device).T
edge_index_final = to_undirected(edge_index_final)
# Train GCN
opt_gcn.zero_grad()
logits, _ = gcn(node_features, edge_index_final)
loss_gcn = cross_entropy(logits[train_mask], labels[train_mask])
loss_gcn.backward()
opt_gcn.step()
val_acc = (logits[val_mask].argmax(dim=1) == labels[val_mask]).float().mean().item()
if val_acc > best_val_acc:
best_val_acc = val_acc
best_test_acc = (logits[test_mask].argmax(dim=1) == labels[test_mask]).float().mean().item()
patience_counter = 0
else:
patience_counter += 1
print(f"Epoch {epoch:03d} | Val Acc: {val_acc:.4f} | Test Acc: {best_test_acc:.4f}")
if patience_counter >= patience:
S.append(best_test_acc)
break
7. 结论
本论文基于前者的Delaunay三角形的算法特点,引入MLP的主动学习,联合调优。典型的优化论文。
在算法优化上使用了多目标优化函数,在整个网络模型上做了较多的优化工作。
8. 个人感悟
中规中矩的优化论文,这种优化思路很值得学习。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号