论文解读-《Spectral Clustering with Graph Neural Networks for Graph Pooling》

1. 论文介绍

论文题目：Spectral Clustering with Graph Neural Networks for Graph Pooling
论文领域：图神经网络
论文核心：MinCut，值得一读
论文发表：ICML 2020
论文代码：https://github.com/FilippoMB/Spectral-Clustering-with-Graph-Neural-Networks-for-Graph-Pooling
论文背景：

2. 论文摘要

谱聚类（SC）是一种流行的聚类技术，用于在图上找到强连接的社区。SC可用于图神经网络（GNN）中，以实现聚合属于同一集群的节点的池化操作。然而，拉普拉斯算子的特征分解是昂贵的，并且由于聚类结果是特定于图的，因此基于SC的池化方法必须对每个新样本进行新的优化。在本文中，我们提出了一种图聚类方法来解决SC的这些局限性。我们对归一化minCUT问题进行了连续松弛，并训练了一个GNN来计算最小化这一目标的聚类分配。我们基于GNN的实现是可微的，不需要计算谱分解，并学习一个可以在样本外图上快速评估的聚类函数。基于所提出的聚类方法，我们设计了一个图池算子，该算子克服了最先进的图池技术的一些重要局限性，并在多个监督和无监督任务中实现了最佳性能。

3. 相关介绍

3.1 背景介绍

最先进的卷积神经网络 （CNN） 交替卷积，从输入信号推断局部特征，池化通过计算附近点的局部摘要对特征图进行下采样。池化有助于 CNN 丢弃对任务来说多余的信息，提供平移不变性，并通过减小中间表示的大小来控制模型复杂性。

图神经网络（GNN）将卷积运算从规则域扩展到任意拓扑和无序结构。 与 CNN 一样，图池化是一项重要的作，它允许 GNN 通过总结局部组件和丢弃冗余信息来学习输入图的越来越抽象和粗略的表示。然而，GNN 池化策略的发展落后于更新、更有效的消息传递 （MP）操作 的设计， 例如图卷积。原因主要是由于难以定义有效支持池化节点特征的图的聚合版本。

最近的 GNN 文献中提出了几种方法，包括利用图论属性预先计算池化图的无模型方法，到基于模型的方法，通过节点特征 的可学习函数执行池化。
现有的无模型方法只考虑图拓扑而忽略节点特征，而基于模型的方法大多基于启发式。因此，前者无法学习如何针对特定的下游任务自适应地粗化图，而后者则不稳定，即使在简单的任务上也容易找到简并解。理论上扎根的、可以适应数据的池化作，任务仍然缺失。

谱聚类 （SC） 是一种众所周知的聚类技术，它利用拉普拉斯谱在图上查找强连接的群落。SC 可用于通过聚合属于同一集群的节点来执行 GNN 中的池化， 尽管基于该技术的方法存在上述无模型池化方法的问题。特别是，SC 没有明确考虑节点属性，拉普拉斯的特征分解是一个不可微分且昂贵的作。此外，基于 SC 的池化方法即使在测试时也必须计算频谱分解，因为每个新图的分解都是唯一的。

3.2 minCut问题

给定一个图 G={𝒱,ℰ} ， K路的归一化minCUT 问题（简称为 minCUT）是通过删除边的最小体积在不相交子集中 𝒱 进行 K 分区的任务。相当于最大化

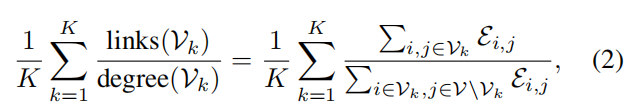
其中分子计算每个聚类内的边体积，分母计算聚类中节点与图形 其余部分之间的边。

设 𝐂∈${0,1}^{N×K}$ 为聚类赋值矩阵 ， $𝐂_{i,j}$=1 如果节点i属于聚类 j ，否则为 0。上面的minCUT问题可以表示为

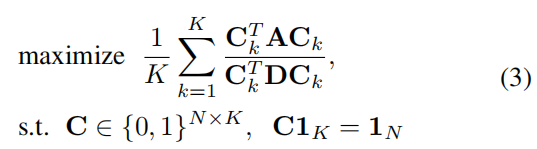
其中$C_k$是C的第k列，由于上述公式的计算是 NP hard的，将其重写为可以在多项式时间内求解的宽松连续公式，并保证接近最优解

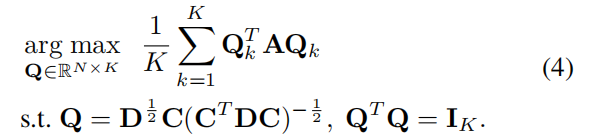
虽然上述最大化公式仍然是非凸的，但存在一个最优解$𝐐^∗=𝐔K​𝐎$ ，其中包含 $𝐔_K∈ℝ^{N×K}$ 对应于最K大特征值的 $\widetilde{A}$ 特征向量，并且 $𝐎∈ℝ^{K×K}$是正交变换。

光谱聚类 （SC） 通过将 k-means 算法应用于 $𝐐^∗$ 行来获得聚类分配，这些行是拉普拉斯特征空间 中的节点嵌入 。SC 的主要局限性之一在于计算 $\widetilde{A}$ 的 𝐐∗ 获得 ，其内存复杂度为 $𝒪​(N^2)$ ，计算复杂度为$𝒪​(N^3)$ 。这阻止了它对大型数据集的适用性。

为了处理 SC 的可扩展性问题，可以通过梯度下降算法来解决上述等式中的约束优化，该算法通过迭代单个复杂度为 𝒪​($N^2$) 甚至 𝒪​(N) 的作来细化解。这些算法通过沿测地线 执行梯度更新，在由正交约束对列 𝐐 引起的流形上搜索解。 替代方法依靠 QR 分解来限制可行解决方案 的空间。

为了学习一个模型，该模型也能为样本外图找到近似的 SC 解，一些工作建议使用神经网络。 有研究训练了一个自动编码器，将 $i^{th}$ 拉普拉斯行映射到第一个 K 特征向量的 $i^{th}$ 分量。

4. 核心算法

本文提出了一种图聚类方法，解决了阻碍 SC 在 GNN 中适用性的局限性。具体来说，我们制定了归一化 minCUT 问题的连续放宽，并通过优化这一目标来训练 GNN 来计算聚类分配。我们的方法学习 SC 找到的解决方案，同时明确考虑节点特征以识别集群。同时，我们基于 GNN 的实现是可微的，不需要计算拉普拉斯的昂贵谱分解，因为它利用了快速计算的空间局部图卷积。这也允许通过简单地评估学习到的函数来对样本外图的节点进行聚类。

算法的框架为：

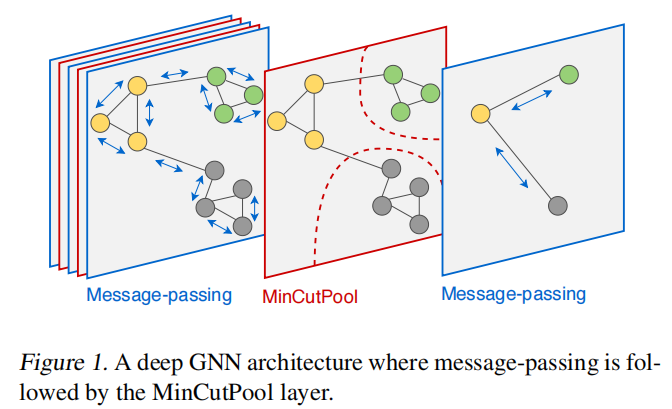
4.1 GNN中的谱聚类

本文提出了一种基于 GNN 的方法，该方法解决了 SC 算法的上述局限性，并根据图拓扑（同一集群中的节点应该是强连接的）和节点特征（同一集群中的节点应该具有相似的特征）对节点进行聚类。我们的方法假设节点特征代表了计算聚类分配的良好初始化。

设$\overline{X}$ 为一个或多个 MP 层产生的节点表示矩阵。我们使用多层感知器 （MLP）计算节点的聚类分配，并在输出层上具有softmax，该感知器将每个节点特征 $𝐱_i$ 映射到软聚类分配矩阵 𝐒 的 $i^{th}$ 行中。

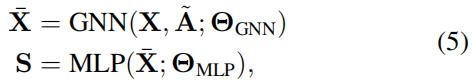
其中 $\theta_{GNN}$ 和 $\theta_{MLP}$ 代表的是可训练的参数。MLP的softmax激活保证并 $s_{i,j} \in [0, 1]$ ，同时强制限制$S1_K = 1_N$ 。
可以在 MLP 中的 Softmax 中添加温度参数，以控制多少 $𝐬_i$ 应该接近单热向量， 即聚类分配中的模糊程度。

参数 $\theta_{GNN}$ 和 $\theta_{MLP}$ 通过最小化由两项组成的无监督损失函数 $L_u$ 联合优化。

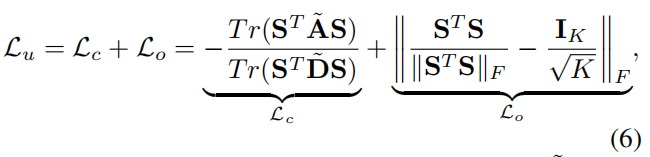
其中 $∥⋅∥_F$ 表示 Frobenius 范数， $\widetilde{𝐃}$ 是 的 $\widetilde{𝐀}$ 次数矩阵

传统的 SC 需要计算每个新样本的光谱分解，而这里的聚类分配是由神经网络计算的，该神经网络学习从节点特征空间到聚类分配空间的映射。由于神经网络参数与图大小无关，并且由于 GNN 中的 MP 操作局限于节点空间并且独立于拉普拉斯谱。

4.2 minCutPool算法

本节提出的方法是一种通用技术专注于在 GNN 中执行池化，引入了 MinCutPool 层。
架构图为

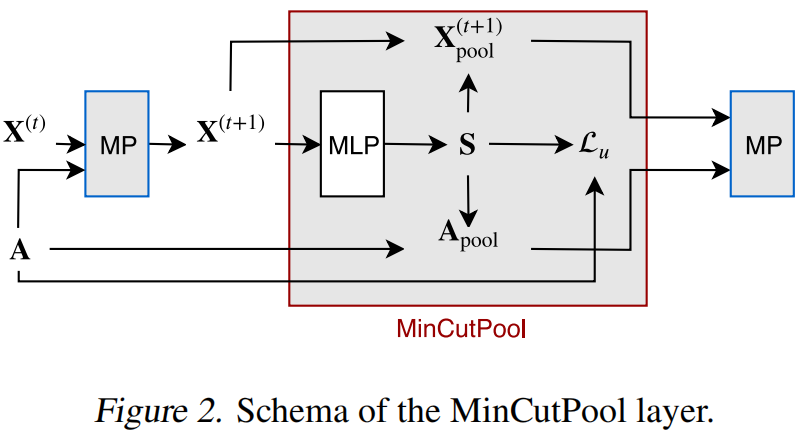
粗化邻接矩阵和合并的顶点特征分别计算为

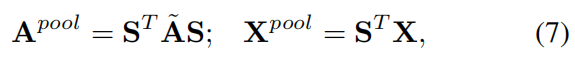
其中，条目 $x_{i,j}^{p​o​o​l}$ 是 $𝐗^{p​o​o​l} \in ℝ^{K×F}$ 聚类 i 中元素之间的特征 j 总和，由聚类分配分数加权。
$𝐀^{p​o​o​l} \in ℝ^{K×K}$ 是一个对称矩阵，其条目 $a_{i,i}^{p​o​o​l}$ 表示聚类 i 中节点之间边的加权和，而 $a_{i,j}^{p​o​o​l}$ 是聚类 i 和 j 之间的边的加权和。
$𝐀^{p​o​o​l}$迹线最大化产生具有许多内部连接且彼此弱连接的聚类。因此，将 $𝐀^{p​o​o​l}$ 是一个对角线主导矩阵，它描述了一个自循环比任何其他连接都强得多的图。
 $\widetilde{𝐀}^{p​o​o​l}$ 通过将对角线归零并应用次数归一化来计算新的邻接矩阵

由于我们基于 GNN 的SC实现是完全可微的，因此 MinCutPool 层可用于构建深度 GNN，从而分层粗略化图表示。
然后，可以通过联合优化 $L_u$ 特定下游任务的任何监督损失来端到端地学习每个 MinCutPool 层的参数。与仅在正交矩阵空间内搜索可行解的 SC 方法相反，$L_o$它只引入了在学习过程中可能部分违反的软约束。这使得 GNN 能够在监督损失和监督损失之间 ℒu 找到最佳权衡，并可以处理具有内在不平衡集群的图。由于是非凸的，因此$L_c$违反正交约束可能会损害与minCUT目标的全局最优的收敛。

计算复杂度： MinCutPool 层的空间复杂度为 𝒪​(N​K)。

无模型池化
这些方法根据拓扑𝐀预先计算粗略图，但没有明确考虑原始节点特征𝐗或GNN产生的中间节点表示。在 GNN 的前向传递过程中，节点特征通过简单的过程进行聚合，并与预先计算的图结构相匹配。

基于模型的池化
这些方法学习如何通过可学习函数来粗略地绘制图形，这些函数将节点特征 𝐗 作为输入，并通过针对任务和手头数据优化的权重进行参数化。虽然更加灵活，但基于模型的方法大多基于启发式方法

DiffPool是一种池化方法，它使用 MP 层来计算输入图的聚类。DiffPool 是端到端学习池化算子的首批尝试之一，并通过最小化聚类分配的熵和链路预测损失来正则化。

5. 实验设置

同时考虑有监督和无监督任务，以将 MinCutPool 与传统 SC 和其他 GNN 池化策略DiffPool算法，进行比较。

5.1 在无监督任务上

实现一个单层 GNN，然后实现一个单层 MLP 来计算 𝐒 ，并通过最小化 $L_u$ 来训练整体架构。
为了进行比较，基于 DiffPool 配置了类似的 GNN 架构，其中优化了辅助 DiffPool 损耗，而没有任何额外的监督损耗。我们还考虑了 SC 类似的聚类，这些聚类基于图谱。

合成网络上的聚类
考虑两个简单的图表：第一个是具有 6 个社区的网络，第二个是常规网格。邻接矩阵 𝐀 是二进制的，特征 𝐗 是二维节点坐标。结果如图

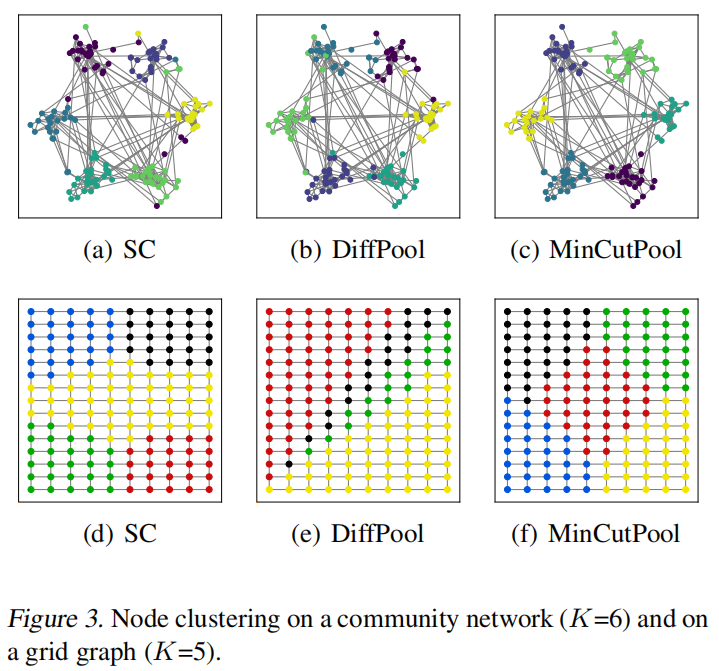
5.2 图像分割

给定一张图像，我们使用过度分割过程 生成的区域作为节点构建了一个区域邻接图。
使用的 SC 技术是递归归一化切割， 它递归地对节点进行聚类，直到收敛。对于 MinCutPool 和 DiffPool，节点特征由每个过度分割区域的平均颜色和总颜色组成。我们将所需集群的数量设置为 K=4 。

完备性分数CS和归一化互信息NMI的指标：为了评估每种方法生成的分区，来检查聚类分配和真实标签之间的一致性。

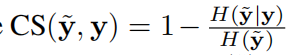
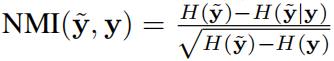
三个算法的比较如下

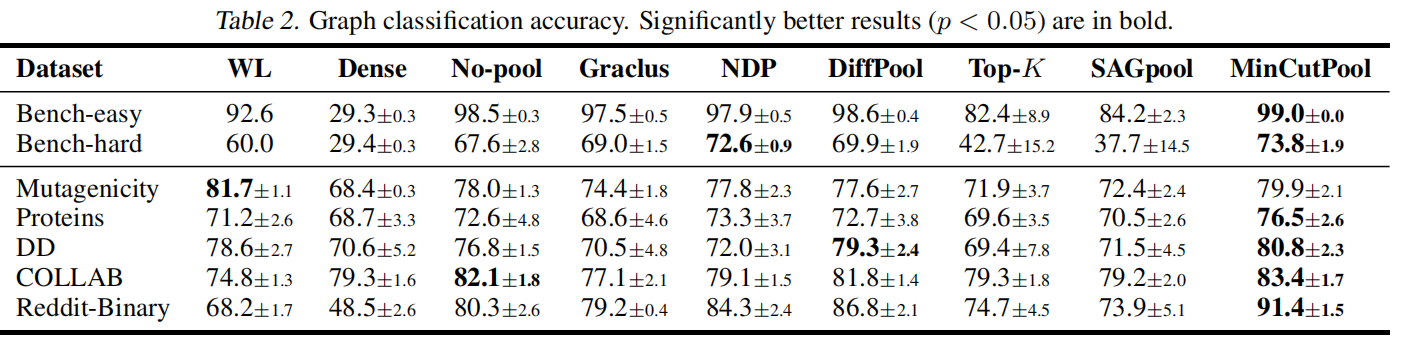
5.3 有监督的图分类

选择对应图分类任务的数据集，选择一个固定的网络模型

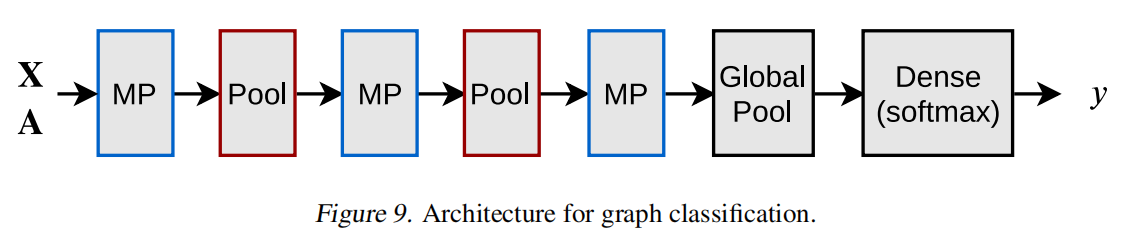
然后针对其池化层进行替换，所有的池化层都设置为降低为一半的参数。

6. 总结

针对谱聚类算法的重要局限性，提出了一种深度学习方法，并设计了一种图神经网络的池化方法，克服了现有池化算子的缺点。结合了图论方法的优点和可学习方法的自适应能力。我们在无监督节点聚类任务上测试了我们的方法的有效性，并且在几个流行的基准数据集上测试了监督图分类任务。结果表明，MinCutPool的性能明显优于现有的GNNs池策略。

7. 个人感想

启发性的SC，主要是解决传统谱聚类的局限性。可以理解为使用额外信息来进一步优化聚类，让下游任务可以表现更好。