论文解读-《The Effectiveness of Curvature-Based Rewiring and the Role of Hyperparameters in GNNs Revisited》

1. 论文介绍

论文题目：The Effectiveness of Curvature-Based Rewiring and the Role of Hyperparameters in GNNs Revisited
论文领域：图神经网络
论文发表：LoG 2024 Oral
论文背景：

2. 论文摘要

消息传递是图神经网络（GNN）中的主导范式。然而，消息传递的效率可能受到图拓扑结构的限制。当信息在传播过程中因在通过瓶颈时被过度压缩而丢失时，就会发生这种情况。为了解决这个问题，最近的努力集中在图重新布线技术上，该技术将源于数据的输入图和执行消息传递的计算图断开连接。一个突出的方法是使用离散图曲率度量，其中已经提出了几种变体，来识别瓶颈并围绕瓶颈重新布线，从而促进信息传播。虽然合成数据集中已经证明了过压制，但在这项工作中，我们重新评估了基于曲率的重新布线给现实世界数据集带来的性能提升。我们发现，在这些数据集中，在重新布线过程中选择的边缘不符合识别瓶颈的理论标准。这意味着它们在消息传递过程中不一定会过度压缩信息。随后，我们证明了这些数据集上的SOTA精度是源自超参数扫描的异常值——包括用于训练的超参数和与重新布线算法相关的专用超参数——而不是一致的性能增益。总之，我们的分析对基于曲率的重新布线在现实世界数据集中的有效性进行了细微差别，并为评估GNN精度改进的方法带来了新的视角。

3. 相关介绍

3.1 图的离散曲率的概念

离散的曲率概念可用于检测图中的瓶颈位置，从而开发出诸如随机离散Ricci流等算法图重连算法。
里奇曲率描述的是两个很接近的边的相交程度，要么发散（负曲率），要么保持平行（零曲率），要么收敛（正曲率）。突出的例子是双曲空间（负曲率）、欧几里得空间（零曲率）和球面（正曲率）。
这些空间的图论对应物是树、四环和三角形。离散曲率概念本质上捕捉了这类结构在给定边周围的分布规律。直观来说，负曲率边在其局部邻域中呈现出更接近树状的结构，因此容易导致信息过度压缩。

平衡福尔曼曲率的定义为

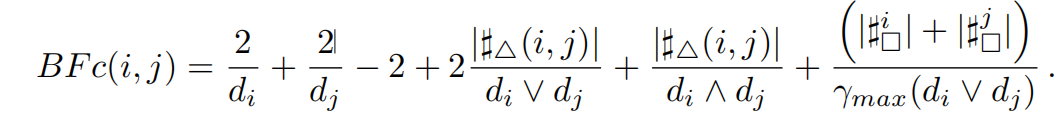
如果min($d_i$, $d_j$) = 1则有 BFc(i, j) = 0。
其中，$d_i$表示的是节点i的度。

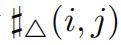
表示的是节点i和j的共同邻居节点

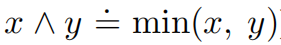
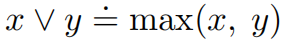
位于i处的邻居节点构成一个不含内部对角线的四循环，表示为

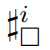
针对原有的平衡福尔曼曲率的定义问题，本文提出的修改后的平衡福尔曼曲率的定义为

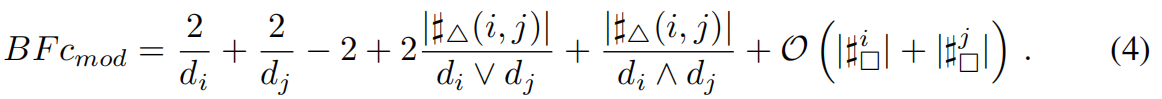
还有，JLc曲率的定义为，（其中为节点i和j间的边的曲率，且$S_+=max(s,0)$）

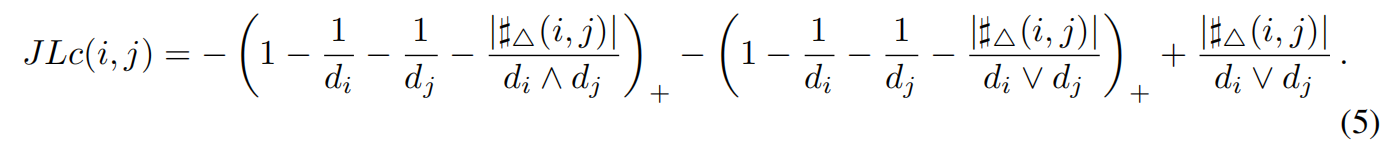
增强福尔曼曲率AFC，有两个变种。对于只有三循环的分布来说，有

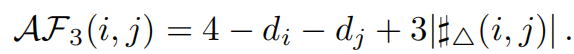
对于四循环分布有

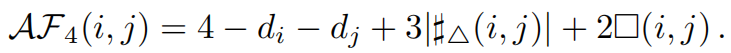
3.2 本文贡献

1，文章的目标是分析基于曲率的图重连算法的有效性，来提高算法在非人工合成数据集上的表现。
2，通过分析超参数扫描的作用，解释了图重连的算法的作用，但是有些效果是得益于超参数调优中的异常值，我们的研究对图数据集的重连方法有效性提出质疑，并为后续探索如何评估GNN改进效果、以及如何在合成数据集之外实现理论与实验的结合提供了研究起点。

4. 曲率和过度挤压问题

根据著名的切格不等式，切格常数可以通过谱间隙来近似计算，即归一化图拉普拉斯矩阵的第一个非零特征值。诸如光谱间隙等全局性测量方法并不能传递关于局部瓶颈位置的信息，因此不一定有助于缓解过度压缩。
基于之前的结论，一个非常负的平衡福尔曼曲率的边是导致过度挤压的原因。本文给出理论4，说明了负曲率的边会引发其周围一大群的节点的扭曲信息。

上述定理4给出了一个理由，在负曲率边周围重新构建图（添加三角形或四环，这些结构会带来正向贡献），因为这会增加δ，从而软化方程8中的边界。其中的集合$Q_j$被明确构建为与边i∼j周围树状结构对应的j的邻居，而平衡福尔曼曲率使我们能够控制从节点i沿边i∼j向这些邻居传递的信息流。

4.1 图重连算法

图重连技术的核心理念在于，通过将输入（真实）图与用于计算任务的图解耦，可以找到缓解前一节提到的过度压缩和平滑问题的方法。

4.2 标准基线数据集中缺乏有效的负曲率边

满足曲率的条件为：

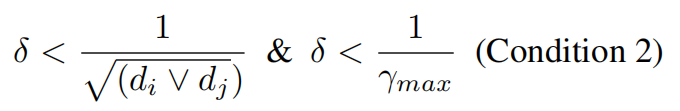
发现上面的基于度的曲率计算太严格，采用更宽松的条件

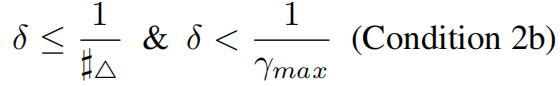
采用新的条件后有更多的边被选中

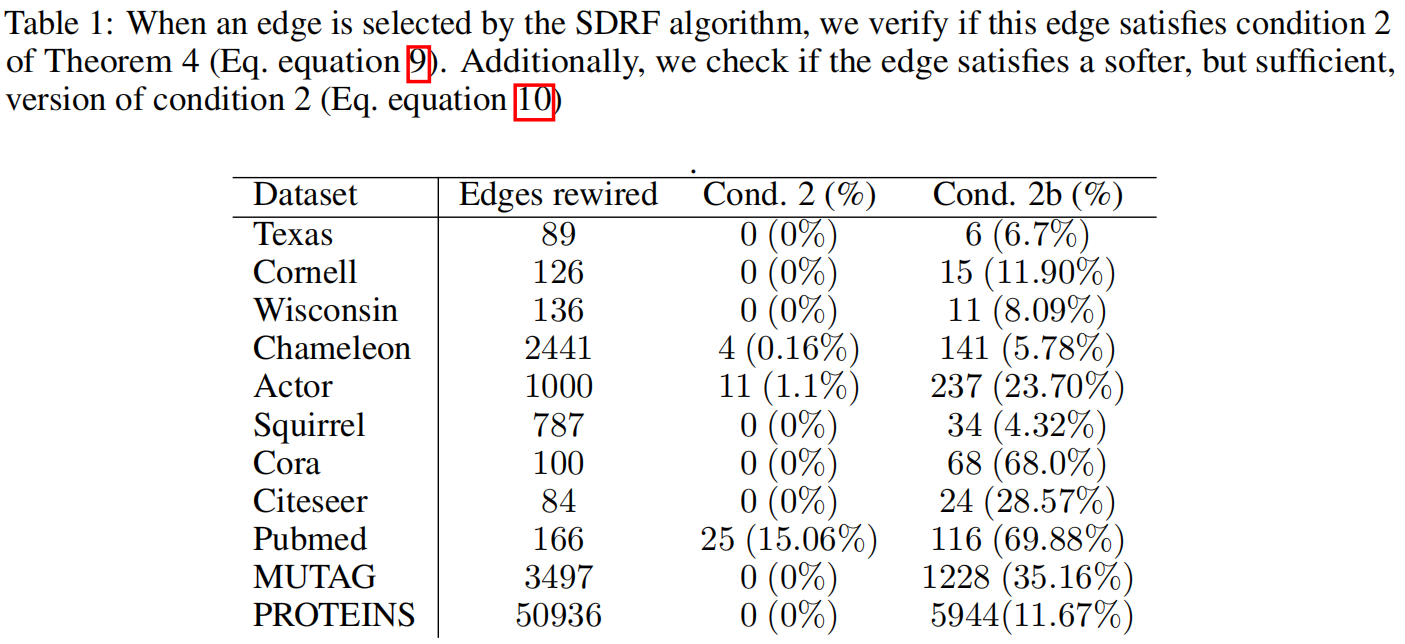
但是新的条件下，会发生一些边满足了条件2但是不满足条件2b的情况，这个在一定程度数上减少了对瓶颈的解释。
对多个数据集的实验数据为

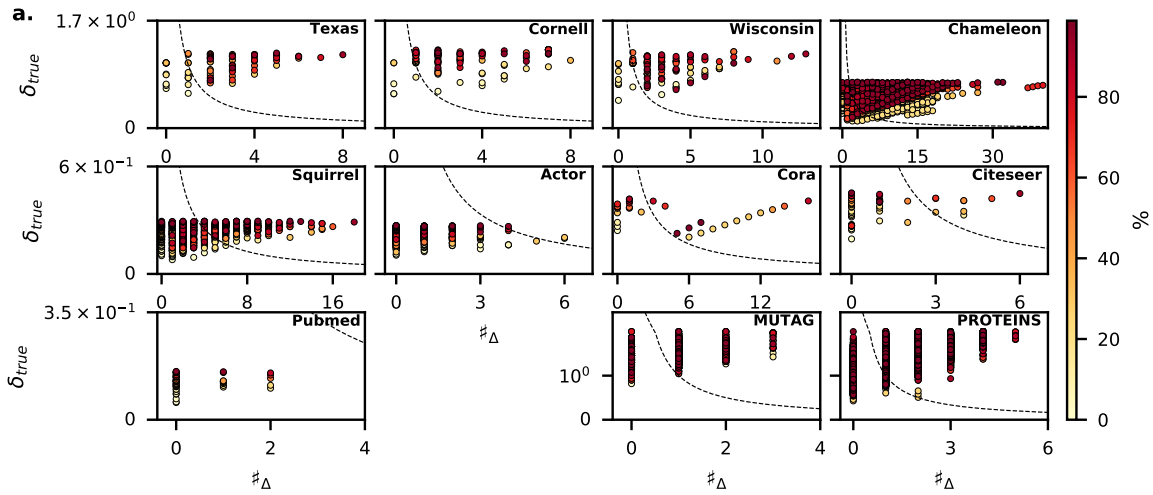
4.3 图重连的超参数依赖

首先是GNN训练的超参数，如学习率，隐藏层，隐藏维度等，其次是SDRF算法的，最大迭代次数，temperature，曲率阈值。虽然超参数的调节是一个重要的部分，但是评价算法不应该从超参数层面来。
所以使用超参数扫描的方式来对各个曲率的算法进行对比，选择每个算法表现最好的实验结果来进行对比。

4.4 实验设置

为了分析不同的曲率在节点分类任务上的效果，使用9个数据集来验证。
数据集分别是：Texas，Cornell，Wisconsin，Chameleon，Squirrel，Actor，Cora，Citeseer，Pubmed。
在图分类任务上使用数据集：MUTAG，PROTEINS

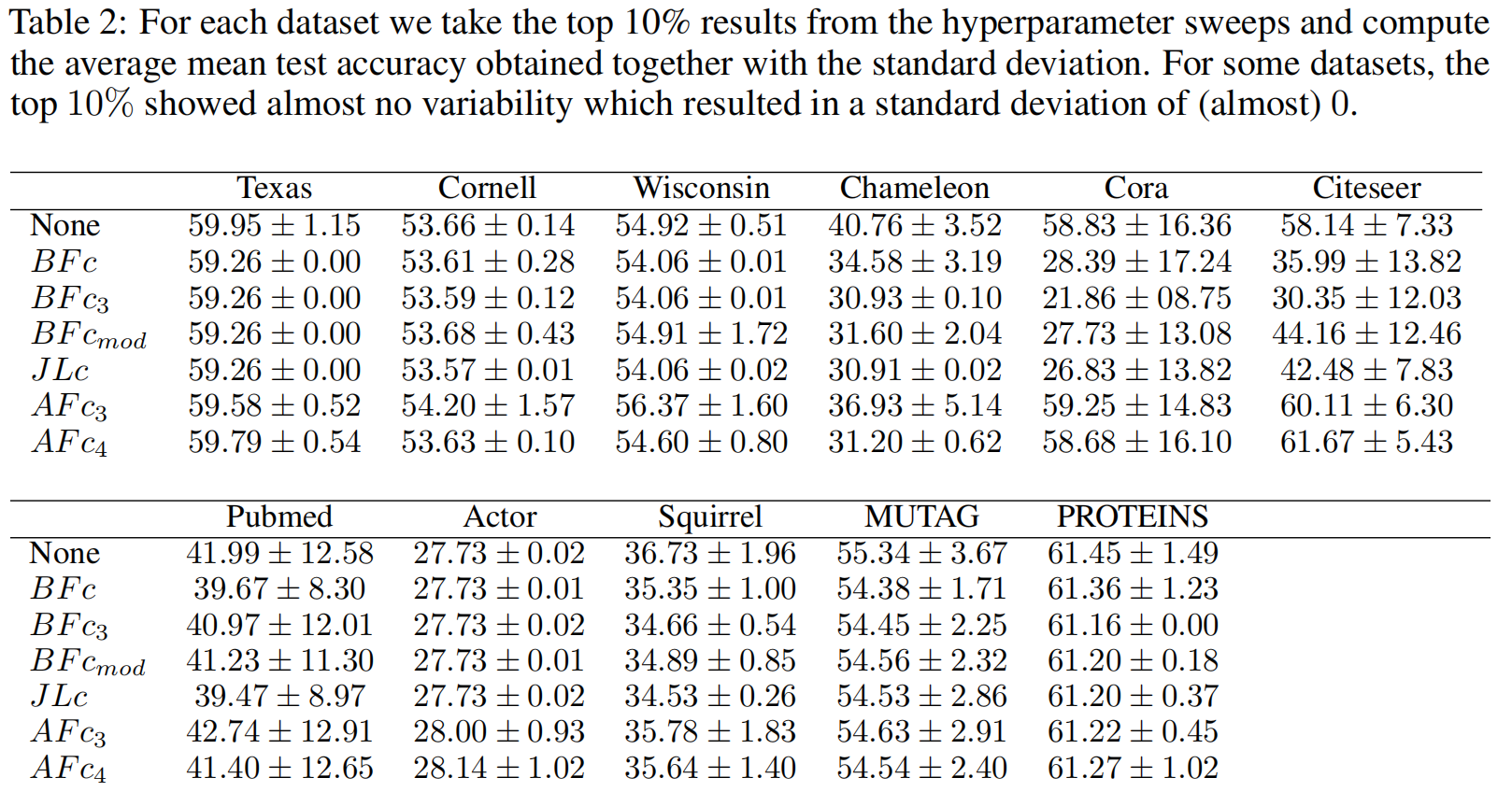
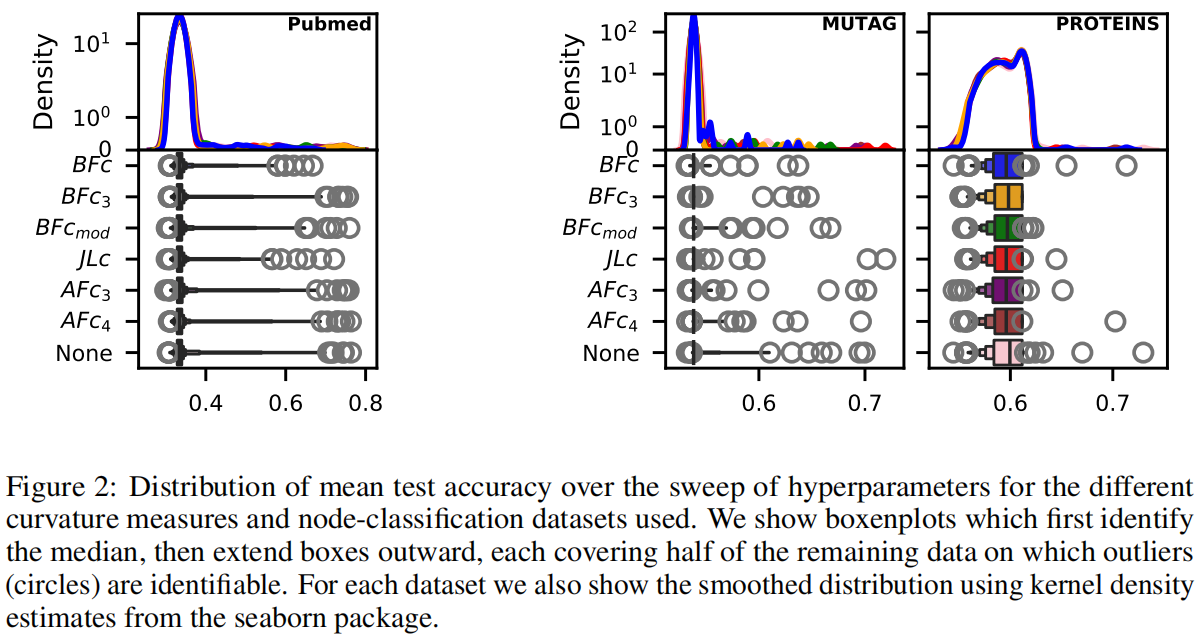
第一个观察是在所有数据集中，没有任何曲率度量能够持续将平均测试准确率的分布从“无”分布（即不进行任何重连）中偏移。
实验也说明了AFC的效果最为显著，但是在严格意义上的统计来说，AFC比None并没有显著的性能优势。

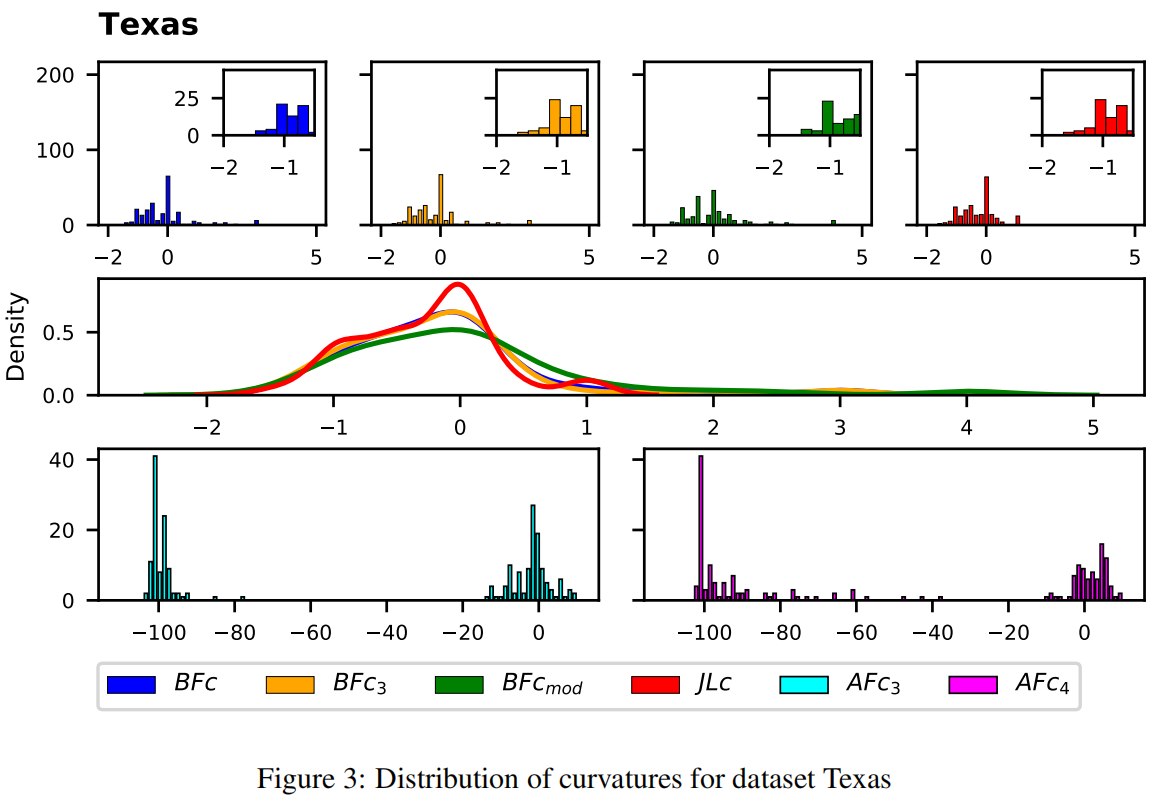
在Texas数据集上的曲率分布情况

5. 总结

全文没有给出新的算法，而是指出了之前基于曲率的算法和现实数据集上的一些问题，通过替换不同的曲率计算公式，发现处理后的数据集得到的实验效果，在跟None环境下比较并没有显著的优势。

6. 个人感悟

论文不一定要提出更好的算法，可以是基于目前的算法，深入研究，并建立一套分析模式和实验来分析当前的算法，并从中得到有意义的结论即可。