论文解读-《Graph Attention with Random Rewiring》
1. 论文介绍
论文题目:Graph Attention with Random Rewiring
论文领域:图神经网络,图重连算法
论文发表:ICLR 2025
论文背景:

2. 论文摘要
图神经网络已成为图结构深度学习的基础。现代GNN的主要模式包括消息传递、图形重布线和图形转换器。本文介绍了一种新的GNN结构——基于注意力的随机结构图重布线(GRASS),它综合了这三种模式的优点。GRASS通过叠加一个随机规则图来重新布线输入图,增强了远程信息传播,同时保留了输入图的结构特征。它还采用了一个独特的加法注意机制为图结构数据定制,提供了一个图归纳偏见,同时保持计算效率。我们的实证评估表明,GRASS在多个基准数据集上取得了最先进的性能,证实了其实际有效性。
3. 相关介绍
3.1 背景介绍
虽然Graph Transformer在处理GNN的欠可达,过度平滑,过度挤压问题有着良好的表现,然而,许多GT由于依赖二次时间复杂度的Transformer结构而面临可扩展性挑战,这使得难以推广到大型图中。
为了解决复杂度问题,线性时间的GPS+Transformers MPNN给出了解决方案,时间复杂度为O(|V|+|E|);另一个算法 Exphormer ,产生了图的稀疏化的Transformers的解决方案。
3.2 本文贡献
1,致力于设计一种GNN,整合消息传递所提供的图归纳偏差、通过图重连实现的信息流优化,以及注意力机制的表征能力。
2,根据上面的三个原则,提出了一个GRASS算法,Graph Rewiring Attention with Stochastic Structures,
3,本文证明了a),将图重连算法和消息传递相结合的直观效果与实证有效性,b),针对图结构设计的加性注意力机制比Transformer风格的点积注意力的架构更有优势,c),随机重连算法的消息传递与GT之间的关联。
4,实验证明了GRASS的有效性,获得了SOTE效果。
3.3 图重连算法
虽然图重连技术通过改善图连通性来增强消息传递神经网络(MPNNs)的信息传播能力,但这种方法可能损害图结构的信息性特征,从而削弱其归纳偏置。
3.3.1 GAT算法
在理论层面,一个MPNN的表达能力是无法超过WL图同构性测试的。GT借助Transformer架构让MPNN能够超越局限。不需要依靠节点邻居间消息传递,GT能够促进所有节点间的同步注意力机制,不受图结构的限制。然而,将图归纳偏置整合到这些Transformer模型中颇具挑战性,因为它们最初是为欧几里得数据设计的。
3.3.2 图编码
图编码算法,通过整合结构信息到边和节点中,提高了GNN的表达能力。如LapPE(图拉普拉斯位置编码)和RWSE(随机游走结构编码)。
4. GRASS的设计
4.1 设计目标
围绕GNN的关键特性,主要聚焦节点和边的处理,同时兼顾可扩展性。
节点方面
- 置换等变性:不同于句子的token或图像的像素,图中的节点是无序的
- 有效的消息传递:需要面对长距离的节点间消息传递
- 选择性的聚合方式:模型应该只聚合相关节点和边的信息,MPNN通常聚合到其他无关的节点边信息,从而导致了过度平滑问题。
边方面:
- 关系的表征:模型应该可以表达节点与边的关系。除了输入图边特征所表示的语义关系外,结构关系可通过模型添加的边编码来表征。为了让模型理解节点间的关系,边表示应整合来自边特征和边编码的双重信息,并通过网络层进行有效利用。
- 方向性保持:许多图的边是有向的,模型应该保持和使用边的方向性信息。
可扩展方面:
- 计算高效:我们允许模型不受此限制地预处理数据以捕捉关键结构特征,只要模型的不可预计算步骤保持O(|V| + |E|)时间复杂度。可预计算操作每个数据集只需执行一次,与训练次数和轮数无关,从而降低其对整体效率的影响。
4.2 算法结构
算法的结构图,可分为预计算好的和真正需要启动训练两个部分
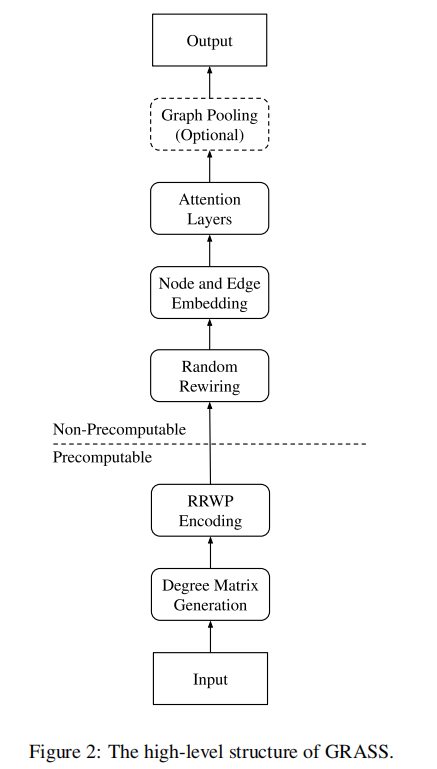
在训练前,可以预计算度矩阵和图的随机游走概率;在每次训练迭代中,GRASS随机重连图结构,对节点和边重编码,将图结构数据通过多个注意力层进行处理,生成具有相同结构的输出图。对于需要图级别表示的任务(如图回归和图分类),需对输出图执行池化操作以获得单一输出向量。
4.3 图编码
GRASS算法使用了RRWP相关随机游走概率编码和DE度编码来表示结构关系。
RRWP编码:是一个理论和实际应用中具有高度表达性的工具。
RRWP具体步骤:
第一步,首先计算随机游走概率,需要获得转移矩阵T,其中Tij代表从节点i到j的一次随机游走的概率。
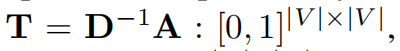
其中D是度矩阵,A是邻接矩阵。
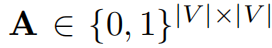
第二步,T的多次幂可以组成RRWP张量P,代表多次随机游走的叠加概率。
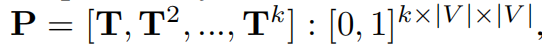
第三步,针对张量P,对角线的Pii,可以作为节点编码,其他为边的编码。
所有节点编码都经过批量归一化(BN)处理以改善其分布,同时批量噪声也充当正则化器,能增强模型对输入图中结构噪声所产生的随机游走概率中噪音的抵抗能力。
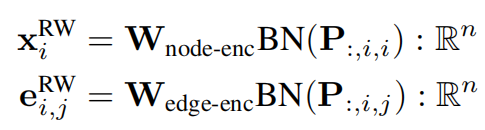
为了计算高效的要求,慢于O(|V|+|E|)的操作需要提前计算。而P是可以提前计算得到,且只需要计算一次。因为P只依赖于原始的邻接矩阵A。
4.4 度编码
对于度数比较小的数据集,模型可以学习到节点的度为一个嵌入张量E,
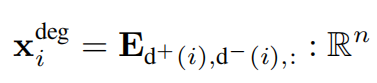
对于度量大的数据集,可以更高效学习到一个线性的层
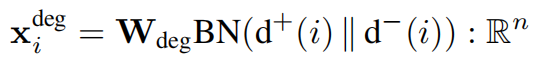
编码的应用
在进入注意力层之前,RRWP编码会被同时添加到节点特征和边特征中(包括通过散发重连添加的边),而度编码仅被添加到节点特征中。
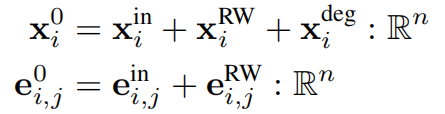
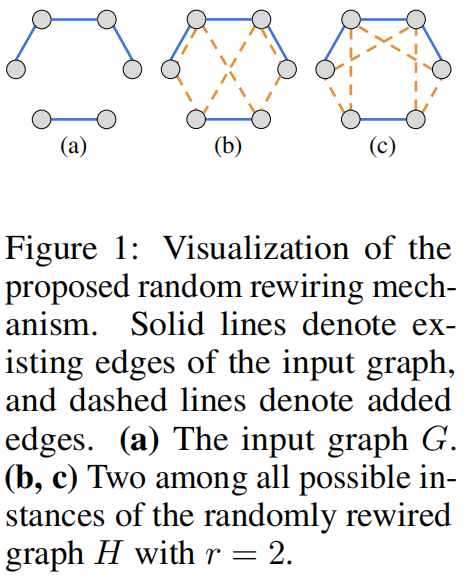
4.5 随机图重连
图直径的影响:将正则图叠加到输入图上可显著减小其直径。因为正则图的直径符合
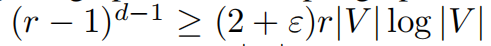
且给图添加边不会增加其直径只会减小。所以,图重连后的图的最大直径是O(logr|V|)。
内部不相交路径的影响
由于过度挤压可归因于通过节点固定大小的特征向量传递过多信息,增加两个节点间内部不相交路径的数量,可能通过允许信息并行通过更多节点传播来缓解过度挤压现象。
谱间隙的影响
叠加随机正则图可能通过增加重连图的谱隙来缓解过度挤压问题。
随机正则图的产生
伪代码为

使用随机permutation算法,可以构建一个随机伪矩阵,为随机正则图。
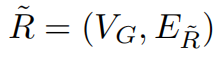
其边的集合是

GRASS希望叠加的图表保持简洁,以避免注意力机制中出现不必要的冗余。所以产生的图的上界需要符合:
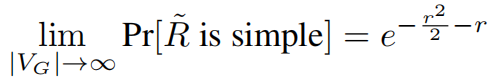
因此,当R˜不符合简单图条件时,我们仅需移除其中的自循环与多重边,从而得到R——该图始终符合简单图标准,但未必具有规律性。
图重连
将新产生的图R和原始图进行融合,得到最终的融合图H。
注意力机制
许多Graph Transformer模仿了为欧几里得数据设计的Transformers结构,GRASS使用了基于注意力的节点聚合,其中注意力分数通过边的MLP聚合器计算得到,这种方式更适合图结构数据。
注意力机制的细节图如下
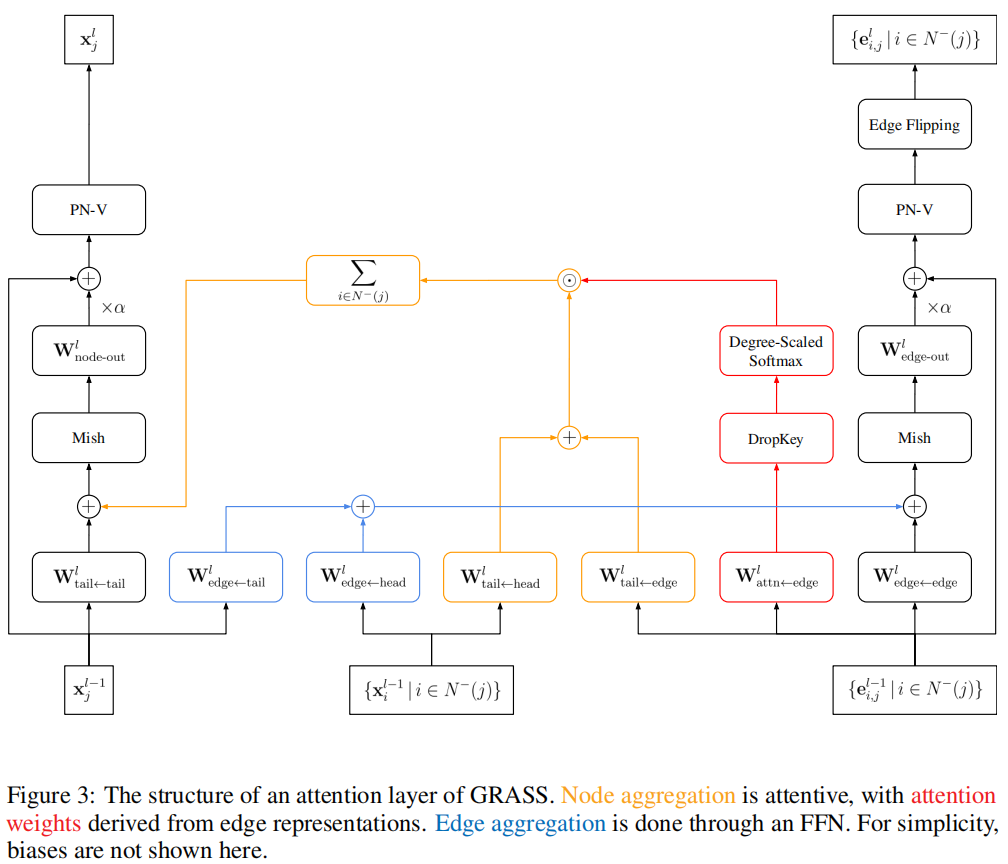
要满足关系表征的需求,边表征必须与节点表征同步更新。与节点不同(其邻域是一组节点),有向边总是包含一个头端和一个尾端,二者构成有序对。无向边可以通过两条方向相反的有向边来表示,这使得我们可以将这一观察结果推广到无向图中。
注意力机制可以写为
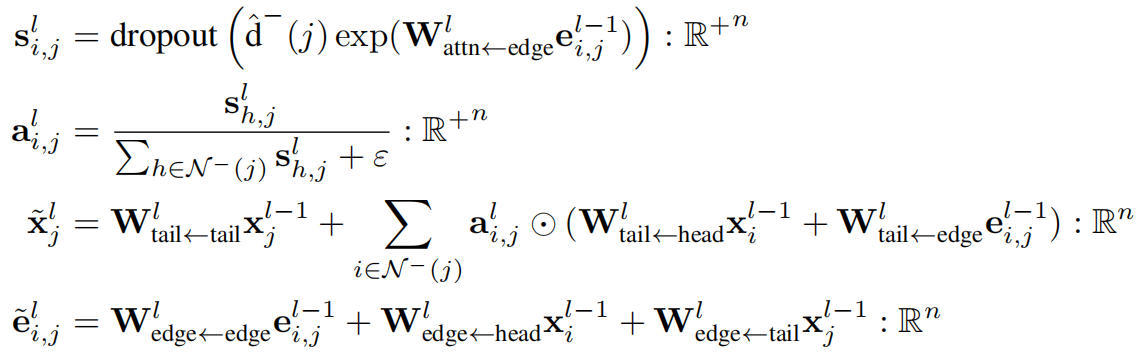
其中 ⭕ 代表的是 Hadamard乘积。
GRASS使用DropKey来作为一个正则化器,在图注意力机制的语境下,该方法能有效降低模型对图中特定边存在的依赖性。Dropkey随机删除一些边,算是随机图重连(只增边)的一个补充。
噪声注入作为一种有效的正则化方法已广为人知,对于图结构数据而言,随机删除边的操作已被证实具有正则化效果。
注意力机制的输出会经过FFN,其中$\phi$是类似Relu的非线性激活函数
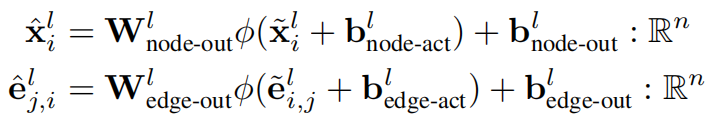
归一化和残差连接
PN-V是Power-Normalization功率归一化的变体,对批量数据的均方根进行标准化处理,相较于BN方法,在处理大方差输入时具有更高的稳定性。
边翻转
为了解决这一问题,我们对每条边的方向进行了跨层切换:在奇数层中,边的方向与重连图H中的边方向一致;而在偶数层中,则将方向反转。这种设计使得模型即使在输入图是有向图时,也能实现双向信息传递,从而显著提升模型的表达能力。
图池化
在图级任务中,需要在NN的输出端进行图池化处理,从而为每个图生成向量表示,捕捉与任务相关的全局特征。GRASS采用求和池化法——这种简单方法虽与韦斯费勒-莱曼检验同样强大,但许多更复杂的池化方法却无法做到这一点。
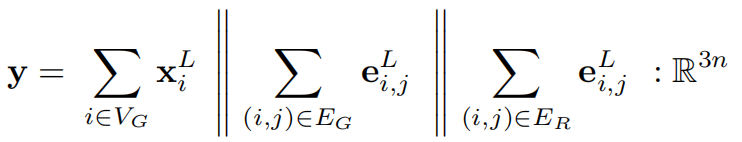
在每一层中,应用一个基于边的表示计算注意力权重的节点聚合器,以及一个用于更新边的表示以反映节点关系的多层感知机边缘聚合器。
4.6 GRASS的解释
假设GRASS的MPNN是在一个噪声图上。原始的邻接矩阵A_G和生成的A_M有
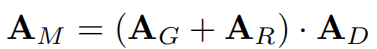
GRASS是一个稀疏的GT,
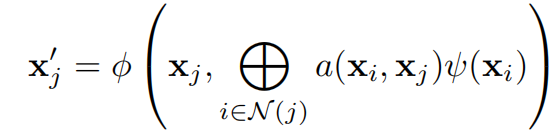
其中 $\phi$ 和$\psi$ 是神经网络模块, $a$是注意力机制权重函数。
我们的设计围绕高效能图神经网络的关键特性展开。该框架主要聚焦节点(N1-N3)与边(E1-E2)的处理机制,同时兼顾所提出模型的可扩展性(S1)要求。
5. 实验设置
5.1 基线数据集实验
在五个GNN的benchmark数据集上,ZINC,MNIST,Cifar10,Cluster,和pattern,还有三个来自LRGB的数据集。
实验数据为
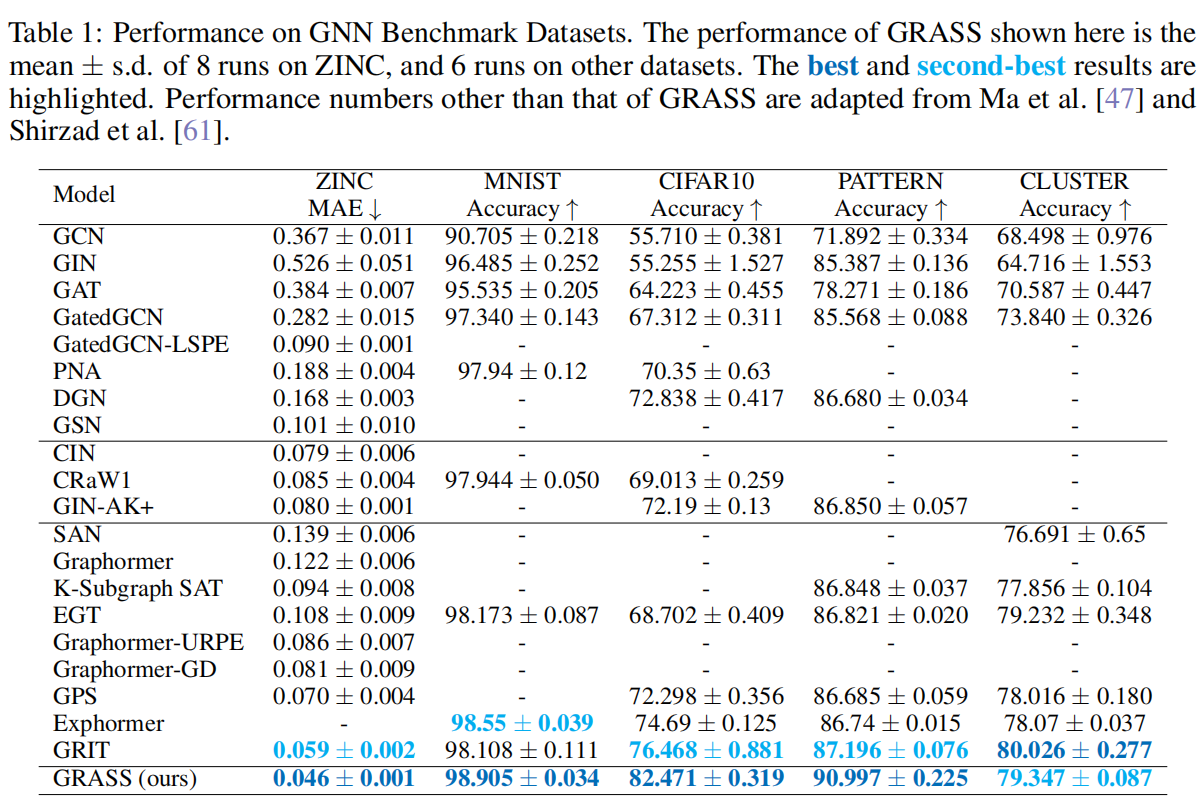

在大部分的数据集上都取得了最好的效果。比第二好的算法GRIT且更低计算复杂度。
5.2 消融实验
证明了整个算法模型的有效性,移除掉算法中的任意一项都难以实现最好效果

验证不同随机正则图的度r对效果的影响

6. 总结
引入注意力机制来优化整个图重连技术,吸收了注意力机制的优点,同时降低了算法的复杂度。
值得好好研读的注意力机制论文。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号