论文解读-《On the Bottleneck of Graph Neural Networks and its Practical Implications》

1. 论文介绍

论文题目：On the Bottleneck of Graph Neural Networks and its Practical Implications
论文领域：图神经网络，图结构学习
论文发表：ICLR 2021
论文背景：

2. 论文摘要

自提出图神经网络（GNN）以来，训练GNN的主要问题之一是它们难以在图中的远程节点之间传播信息。我们对此问题提出了一种新的解释：GNN在跨长路径聚合消息时容易出现瓶颈。这个瓶颈导致指数增长的信息过度压缩成固定大小的向量。因此，当预测任务依赖于远程交互时，GNN无法传播来自远程节点的消息，并且性能较差。在本文中，我们强调了GNN中固有的过度压缩问题：我们证明了瓶颈阻碍了流行GNN在训练数据中拟合远程信号；进一步的研究表明，平均吸收入射边的GNN，如GCN和GIN，比GAT和GGNN更容易受到过挤压；最后，我们指出，先前的工作，广泛调整GNN模型的长期问题，遭受过度挤压，打破瓶颈改善其最先进的结果没有任何调整或额外的权重。

3. 相关介绍

基于消息传递的GNN的每个节点通过聚合来自直接邻居节点的消息来更新本节点的特征。为了能捕获到更远距离的连接的节点的消息，通过堆叠多个GNN层来实现，不同的学习问题需要解决图中节点之间不同范围的交互，这种节点之间需要的交互范围，称之为问题半径。
由于学习问题主要取决于数据集中的短程信息，这就解释了为什么比问题半径更多的层可能是多余的，相比之下，在同样依赖长程信息的任务中，假设性能有限的原因是过度压缩。
为了允许一个节点从半径为K（即跳跃数为K）的其他节点接受信息，GNN需要至少K。否则出席那欠可达问题。
随着层数的增加，每个节点视野中的节点数量指数增长，而每个节点的特征维度是固定的，所以指数增长的信息被压缩为固定长度的节点向量，图无法传播从远处节点流动的消息，只能从训练数据中学习邻居周围的信息。
类似RNN模型的瓶颈问题，传统的seq2seq模型在每一个解码器都有一个瓶颈问题，模型必须把整个输入序列转为一个固定大小的向量。在GNN中，节点包含的视野信息越多，节点的数量越多，包含的信息也多，信息压缩越严重。

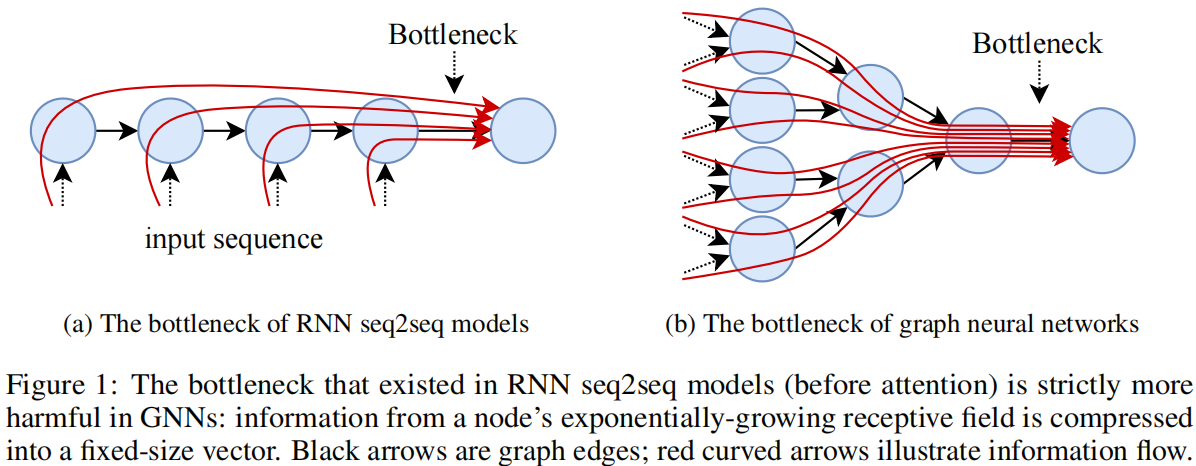
图神经网络难以有效地远距离传播信息或从深层架构中获益，层数增加时性能常下降。GNN深度限制的普遍解释是过度平滑，即节点表示随着层数增加而变得难以区分，但这不能完全解释长距离任务上的问题。现有GNN模型通常无法捕获真实世界图中关键的长距离依赖关系。

4. GNN的瓶颈问题

4.1 定义

可以把一个节点的视野定义为一个集合$N_v^K$的形式，循环定义为：

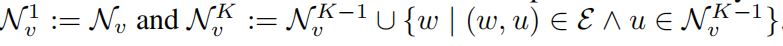
当预测问题依赖节点之间的远距离的作用时，GNN必须具有这些相互作用的估计范围相同的层数，否则这些远处的节点将无法相互作用。

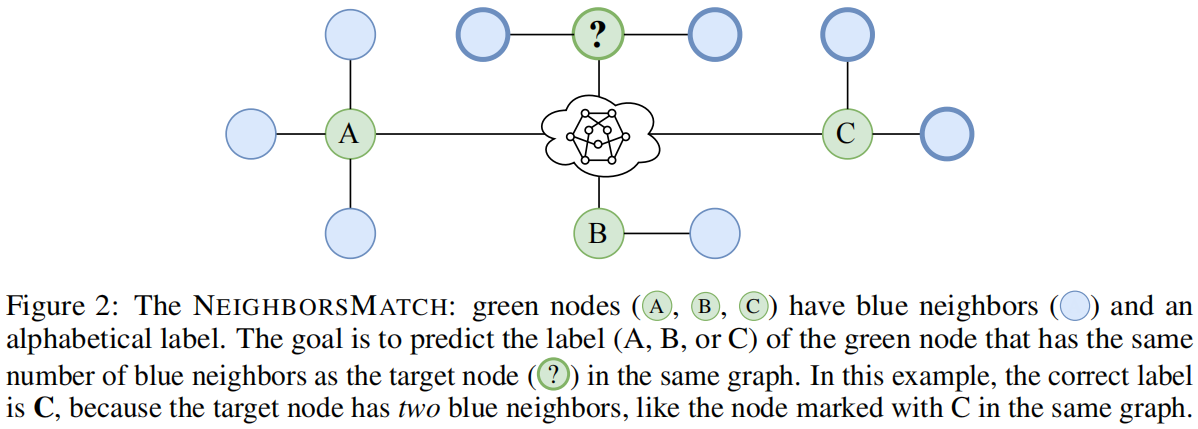
图2中的neighborsmatch问题。绿色节点(A,B,C)有不同数量的蓝色邻居(A)和字母标签。数据集中的每个示例都是一个不同的图，从邻居数量到标签的映射也不同。图的其余部分(标记为)表示一个通用的、未知的图形结构。目标是根据蓝色邻居的数量预测用问号标记的目标节点的标签。在这种情况下，正确的答案是C，因为目标节点有两个蓝色邻居，就像在同一图中标记为C的节点一样。数据集中的每个示例都有从邻居数量到标签的不同映射，因此必须对数据集中的每个图执行目标节点和所有绿色节点之间的消息传播和匹配。
由于模型在预测标签之前必须传播所有绿色节点的信息，因此在目标节点不可避免地会出现瓶颈。这个瓶颈会导致过度压缩，这可能会阻止模型完美地拟合训练数据。

4.2 短范围和长范围的问题

之前的许多的GNN工作都是基于在短范围的局部特征上，其潜在的归纳偏差是节点的局部领域内的邻居节点，且不一定需要长距离的交互。
长程相互作用，因此需要大量的GNN层，由于每个节点的感受野随着层数呈现指数级增长，因此层数越多，过度挤压越有害。但是在本质上是局部问性特征的问题上，瓶颈影响不大，因此GNN只需要几层就可以表现良好。

5. 实验设置

5.1 合成基准

NEIGHBORSMATCHproblem问题从人为设计的直观方式说明过度压缩的受到问题半径的影响程度。这里基于问题半径的变化来观察模型的训练精度，以表明过度挤压会阻止模型在训练过程中学习远距离的信息。

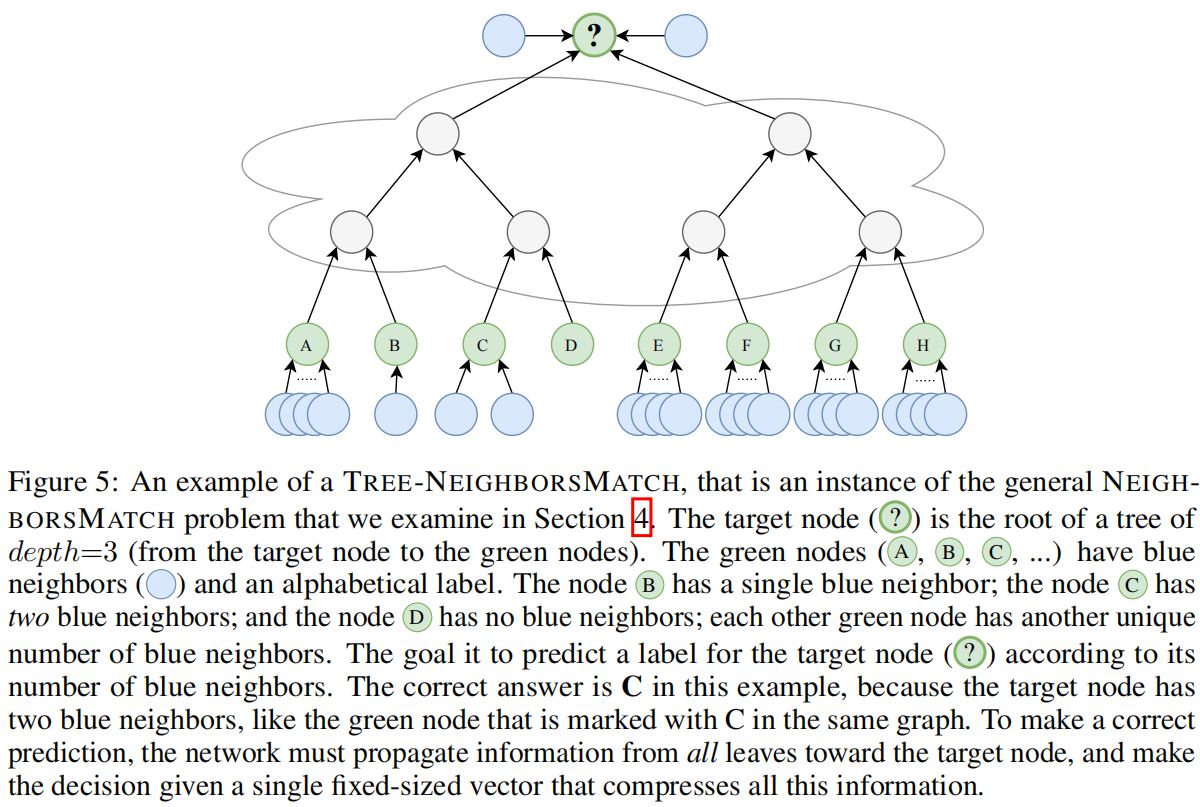
tree-neighborsmatch从单个节点v的角度来看，以树的深度来模拟这种指数增长的视野，有实验结果

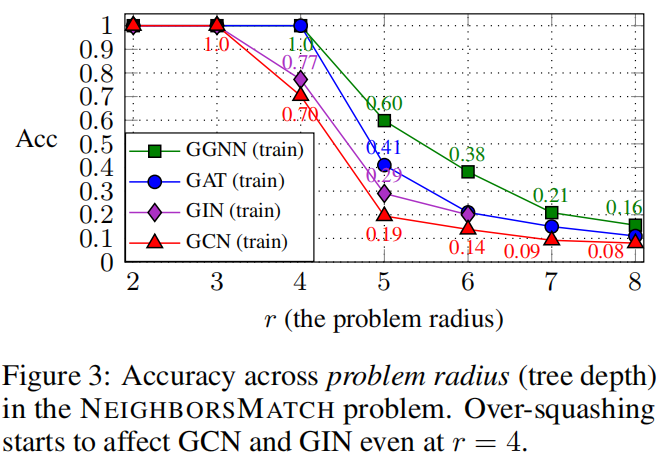
实验结果发现在r=4就开始无法拟合，在r=5开始所有的GNN都无法拟合。
GCN和GIN最多在r=3的时候拟合，GGNN和GAT在r=4的时候仍然拟合，这种差异可以用他们的邻居聚合计算来解释，考虑r步中接收消息的目标节点，GCN和GIN在将所有邻居和目标节点表示相结合之前聚合它们。GAT在给定目标表示情况下使用注意力对传入消息进行加权。
如果所有的GNN都达到了较低的训练精度，基于GNN的模型通常如何拟合远距离的训练数据。

5.2 QM9

如何衡量过度挤压问题 ，从数值的角度，解决过度挤压是否会解决模型训练和预测有帮助。
添加全邻接层FA，来替换GNN的最后一层。全邻接层式一个GNN层，其中每个节点对都有一条边连接。

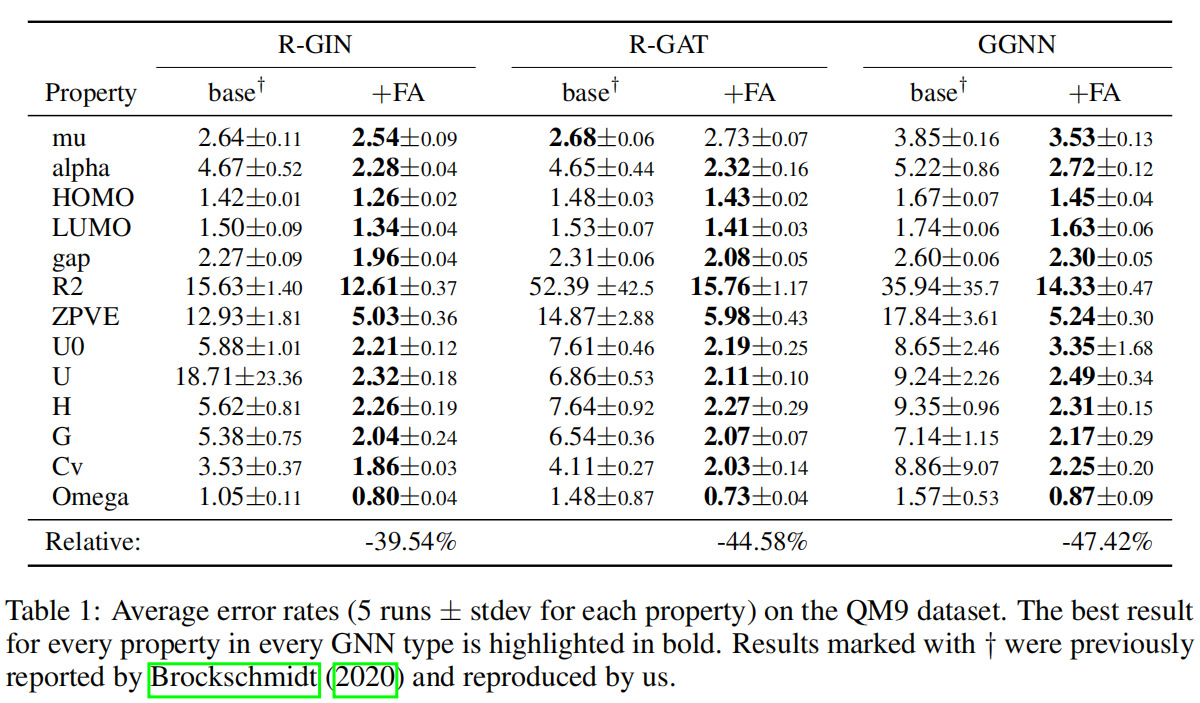
实验数据结果表明，通过将单个层修改为FA层来突破瓶颈，能显著降低错误率。在六种GNN类型上平均降低42%。这些实验清晰地证明了原始GNN模型中存在瓶颈效应。

在更大的模型上是否有同样的效果：在另外一组有着双倍维度的模型上测试，仅仅获得了5.5%的提升。
如果所有图神经网络都能从节点间的直接交互中获益，或许连图结构本身都不再必要？训练了另一组模型，其中所有K层均为全连接层，从而完全忽略原始图拓扑结构；这些模型的误差竟高出1500%（表现更差）。

5.3 消融实验

长距离的长有多长，计算Tree-NEIGHBORSMATCH问题的r有多大。
将此类树的元数记为m（实验中设为2）；计数基数b=2；浮点变量位数f=32；并将GNN的隐藏维度（即节点向量h(v_k)的尺寸）记为d。

在与靶区节点交互并预测标签之前，必须用一个尺寸为d的向量来封装所有绿色节点传递的信息。该向量包含d个浮点元素，每个元素以f位存储。总体而言，这个向量能区分的可能情况数量为b^(f·d)种。该向量能区分的可能情况数量必须大于其在训练数据中可能遇到的不同样本数量，该要求如公式4

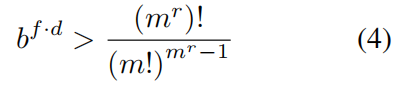
对于二叉树(m=2)和f=32位(b=2)的浮点数值，有公式5.

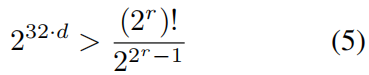
6. 对照实验和验证

1，欠可达和过度挤压：验证了大多数图的直径都在现有层数之内，排除了可达性不足的原因
2，模型容量：将基础的GNN隐藏维度加倍，仅仅带来微小提升，而FA带来了大幅提升，说明瓶颈并不是简单的模型容量问题
3，图结构：使用所有FA层训练的模型表现远不如混合方法，说明了原始图拓扑结构对于大部分计算仍然很重要。

7. 总结

本文引入”过度挤压“作为一种信息论瓶颈，是GNN在长距离任务上表现不佳的主要原因。理论分析表明为缓解过度挤压所需要的隐藏维度存在指数级下限，强调了简单增加 模型容量的不切实际性。提出并实证验证了一种简单的干预措施，即”全相邻层“，通过修改GNN的最后一层，允许所有节点之间相互传递消息，有效打破信息瓶颈，且无需增加新的权重或大量调优。

8. 个人感悟

引入RNN的瓶颈概念，根据对照实验和消融实验来分析，是分析类，验证类的好论文。值得一读。