论文解读-《Dirichlet Energy Constrained Learning for Deep Graph Neural Networks》

1. 论文介绍

论文题目： Dirichlet Energy Constrained Learning for Deep Graph Neural Networks
论文领域：图神经网络
论文发表：ICLR 2021
论文背景：

2. 论文摘要

图神经网络（GNNs）有效地集成了深层结构和拓扑结构建模。然而，现有的GNN在多层次叠加时，由于存在过平滑问题，性能会显著下降。当GNN递归地聚集邻居的表示时，节点嵌入趋向于收敛到相似向量。为了实现深度GNN，最近探索了几种方法。但它们是从卷积神经网络技术或启发式策略发展而来的。深GNNs的设计没有可概括的理论指导原则。为此，我们利用节点嵌入的Dirichlet能量分析了deep GNNs的瓶颈，并提出了一个可推广的原则来指导deep GNNs的训练。在此基础上，设计了一种新型的深度GNN框架——EGNN。它可以根据各层的Dirichlet能量提供上下约束，避免过度平滑。实验结果表明，EGNN通过使用深层实现了最先进的性能。

3. 相关介绍

3.1 背景介绍

一个关键的局限是GNN在有层数达到一定数量后，整个网络的表现会下降明显。实验的经验值是GNN的层数小于3层。随着GNN的层数增加出现的过度平滑的问题，一般的解决方案有特征归一化和残差连接，还有一些启发式策略是随机特征传播和随机丢弃边。
最近的一项研究将Dirichlet能量用于衡量过度平滑问题，基于对节点间距离的衡量。

3.2 本文三个贡献

1，提出了一个通用法则，迪利克雷能量限制学习，基于迪利克雷能量正则化来训练深度GNN。针对每一层定义一个合理的迪利克雷能量限制，基于该约束，可同时loss优化和能量优化。
2，提出了一个新的架构，EGNN，包含三个模块，正交的权值控制，下界残差控制，偏移Relu激活函数。GNN的权值是通过对称矩阵来初始化实现正交的。

3.3 迪利克雷能量限制学习

节点对的距离被广泛用于衡量基于特征相似度的过度平滑问题。
迪利克雷能量的定义为

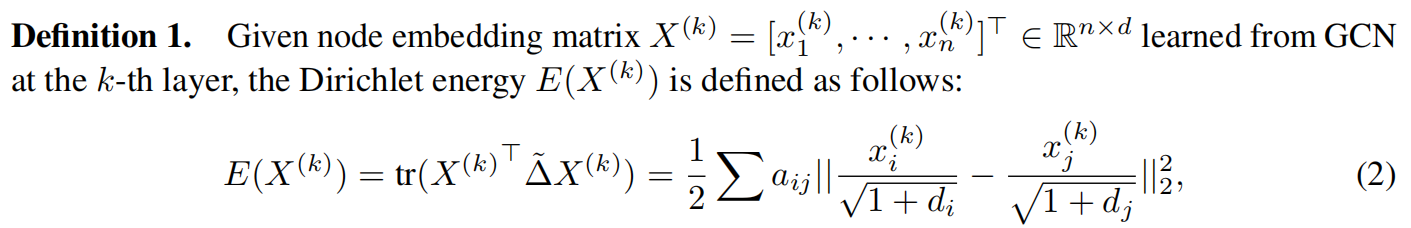
其中$tr$是求矩阵的秩，$a_{ij}$ 是边的权重，$d_i$是节点i的度。
对于迪利克雷能量值，越大则各个特征之间越分开，甚至是同类的节点也弥散开，越小则是各特征挤在一起，即过度挤压现象。
我们需要找到一个度，让不同类别的节点的分开，相同类别的节点靠在一起。

确定迪利克雷能量的边界

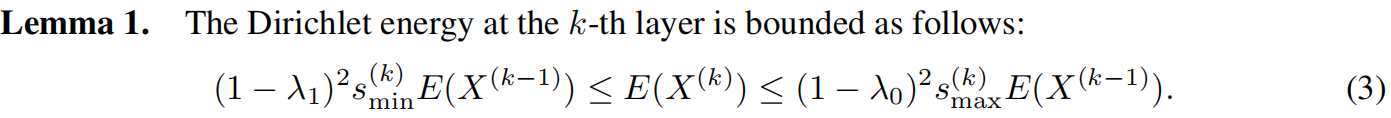
其中$\lambda_1$和$\lambda_0$ 是矩阵$\tilde{\Delta}$的分别最靠近1和0的非零特征值。$s_{min}^{{(k)}$和$s_{max}}$分别是权重矩阵$W^{(k)}$的最小和最大奇异值的平方。
一般现实的图数据，邻接矩阵$\tilde{\Delta}$所得到的特征值的范围是$[0, 2)$。
所以有引理2：

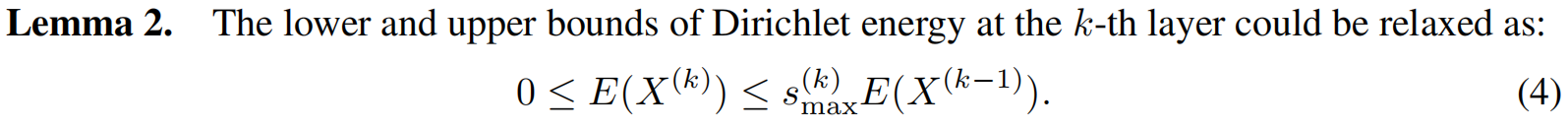
实验中发现深层的GNN一些权重矩阵会逼近0矩阵，那说明其特征值也趋于0，即迪利克雷能量变为0从而产生过度平滑问题。
从而可以有

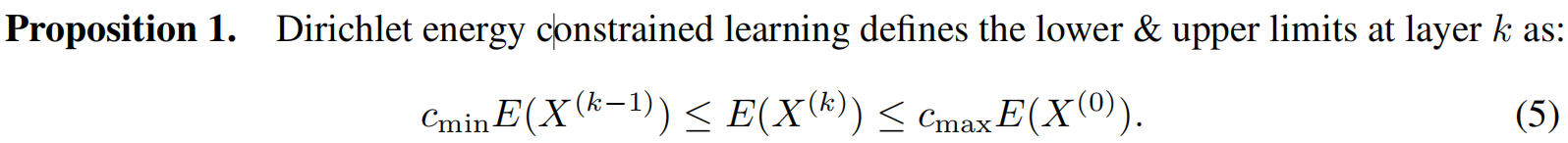
其中$c_{min}$和$c_{max}$是正的超参数。且$c_{min}$满足范围$(0,1)$区间，可以满足限制

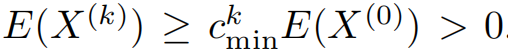
同时 $c_{max}$满足范围$(0,1]$区间，才能避免过度分离。

最终优化问题转为优化loss函数和能量限制

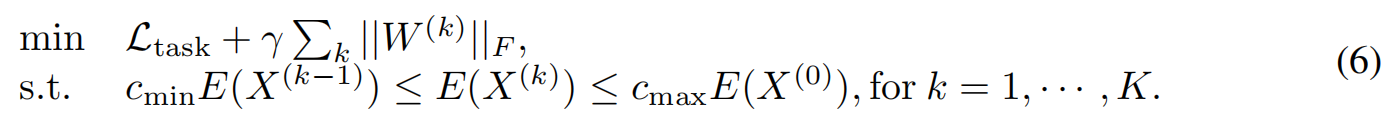
4. EGNN

4.1 正交的权重控制

根据引理2可以知道限制$s_{max}^{(k)}$的值就可以限制迪利克雷能量的上界。传统的权重初始化工具（如 Glorot初始化）没有办法实现限制特征值的范围，这里采用正交初始化，用显式的特征值来进行权值初始化。我们推导出命题2来初始化EGNN所有层的权重$W(k)$及其平方奇异值
命题2为

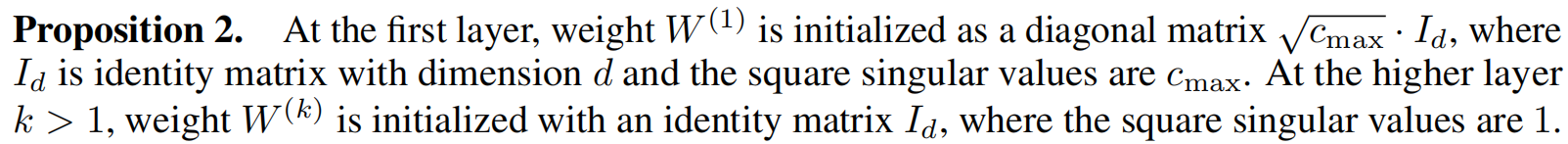
根据上面的命理的初始化方法，可以满足每一层的迪利克雷上限。

正交正则化
为了在训练过程中也保证其满足限制，需要在优化问题中加入正则化项。

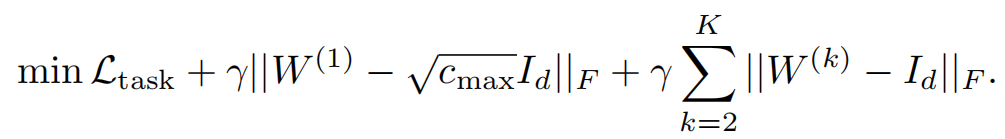
4.2 下界残差连接

上面一章节使用初始化方法和正则化项满足了迪利克雷上界，这个章节来保证下界。根据引理1可以知道下边界是

在密集连接的图中，邻接矩阵的特征值大概率会趋于1，所以尽管$s_{min}^{(k)}$$\leq$$0$，也会让迪利克雷能量小于下界而导致过度平滑问题，为了解决这个问题，引入残差连接

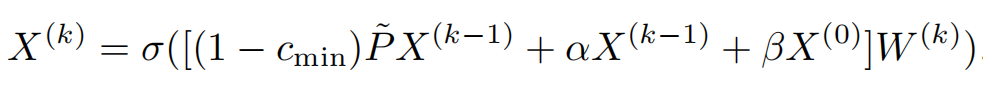
其中$\alpha$和$\beta$是残差连接强度，取决于迪利克雷限制学习的下界，满足$\alpha+\beta$$=$$c_{min}$
如下两个引理，在约束学习中，通过所提出的下界残差连接可以同时满足下限和上限要求。

证明了上界的要求

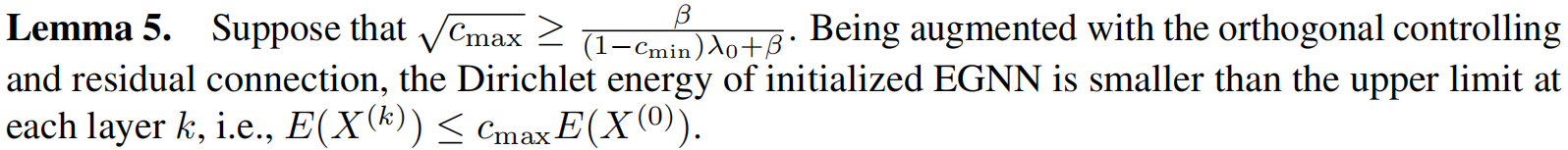
4.3 SRelu激活函数

如果采用常规的Relu函数，因为Relu函数会把负输出置为0，那就意味着每次经过Relu，整个迪利克雷能量会下降。尽管可训练权重和残差连接经过精心设计，下降的迪利克雷能量仍可能突破下限。

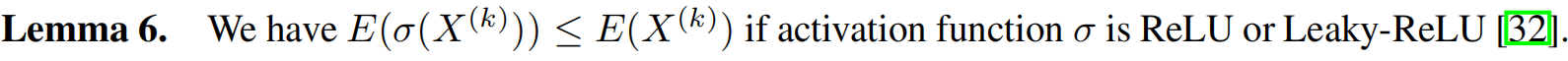
所以，引入一个带偏移的Relu函数

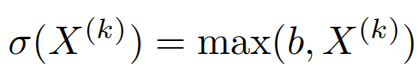
其中b是一个可学习的偏置，在每一层的特征$X^{(k)}$的多个维度共享。
当偏置项b趋近于∞时线性恒等激活近似成立，若节点嵌入小于特定阈值b则激活非线性映射。

4.4 和其他工作的比较

为了训练深度的GNN，也有很多其他的方法来实现。

4.4.1 嵌入归一化

PairNorm算法是通过限制每一层的节点对的距离保持在一个常量范围内，从而克服过度平滑
本文的迪利克雷能量其实也是节点对距离的变种。

4.4.2 边丢弃

随机隐藏一些边，从而让图稀疏化来克服过度平滑问题
在实际应用中，丢弃率必须根据不同任务仔细确定。相比之下，本文方法赋予模型自由度，使其能在较大且适当的范围内优化狄利克雷能量。

4.4.3 残差连接

受CNN的启发，残差连接被应用于保留先前节点嵌入并缓解过度平滑问题。特别是在相关研究中，最后一层的嵌入被完全复用和整合。

4.4.4 模型简化

模型SGC为了避免过度拟合问题来移除了所有的激活函数和训练权重。类似于EGNN的$c_{max}=1$ $b=-\infty$ 的情况。

5. 实验设置

选择的数据集：Cora，Pubmed，Coauthor-Physics，Ogbn-arxiv
选择的基线模型：GCN，PairNorm，DropEdge，SGC，JKNet，APPNP，GCNII。

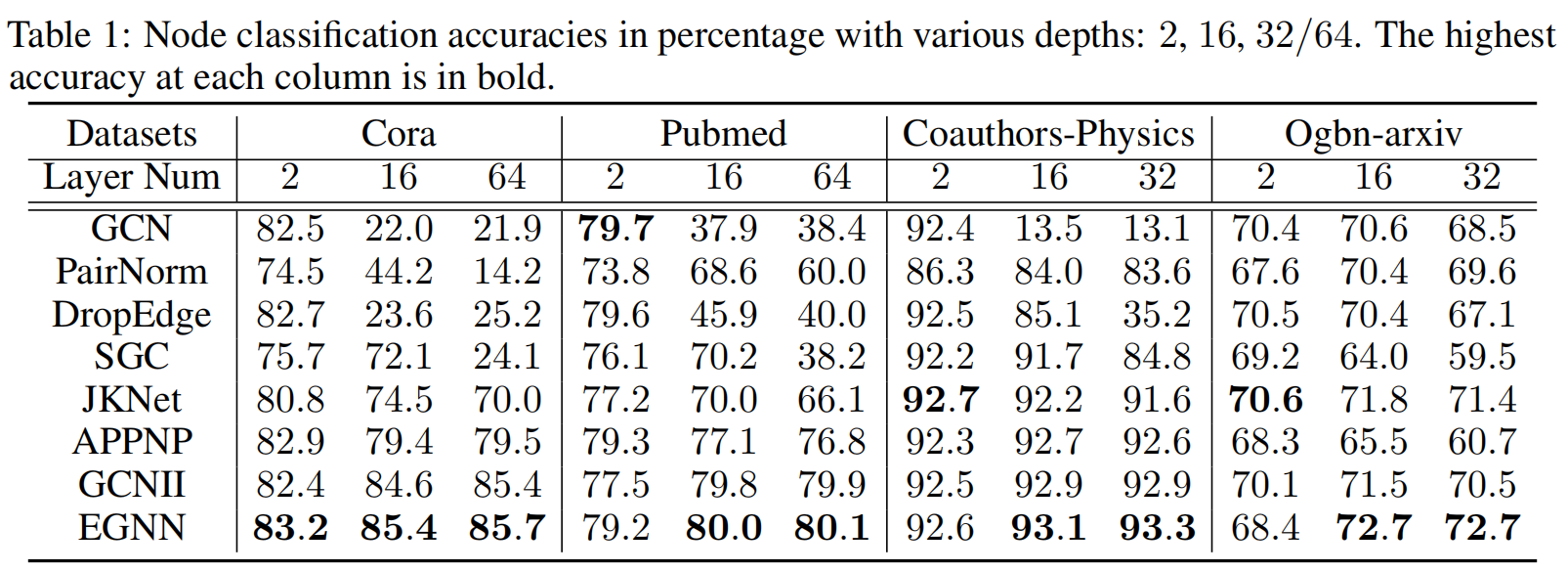
节点分类任务的实验结果

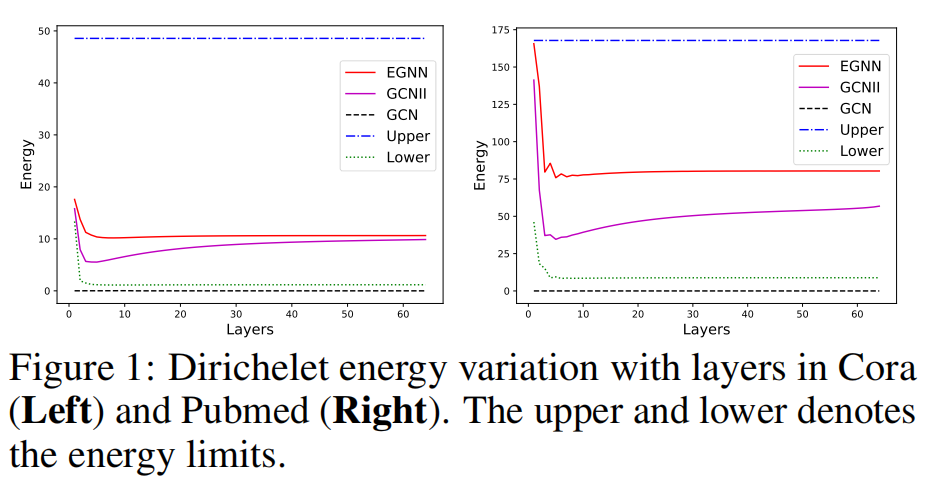
迪利克雷能量的可视化

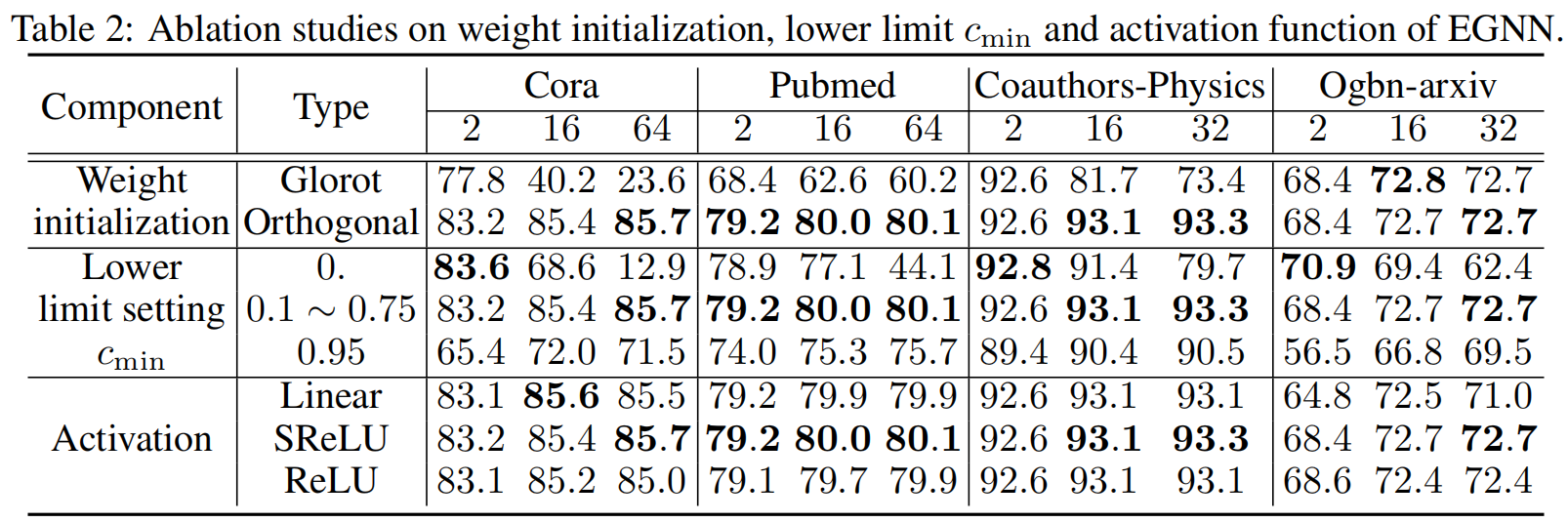
消融实验
对于正交权重初始化与正则化组件，我们将其与传统Glorot初始化和Frobenius范数正则化进行比较和替换
对于下界残差连接，我们选择下界不同的超参数设置$c_{min}$
对于激活函数，对比线性激活函数，SRelu和Relu

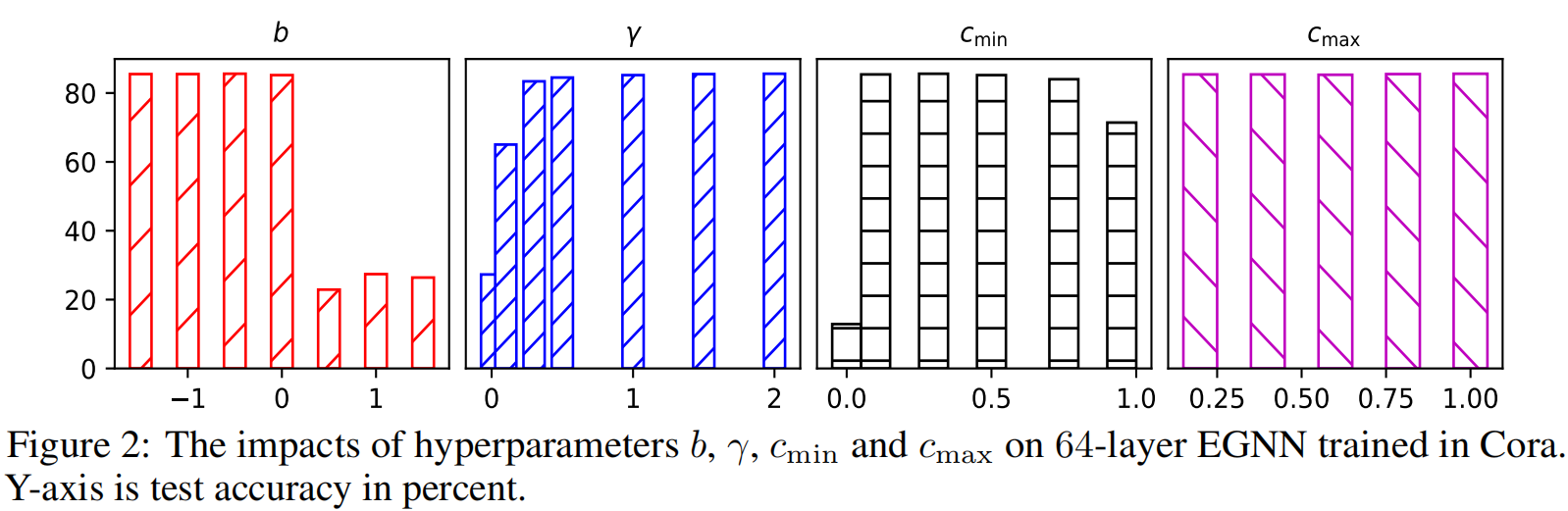
不同的超参数设置下的影响

6. 总结和个人感悟

使用迪利克雷能量来指代图邻接矩阵的平滑度，同时优化损失函数和迪利克雷能量，从优化的角度来解决过度平滑问题的一种。缺点是各项限制太多，每一层的权重都需要维持在区间内，一定程度上降低了通用性，增加了训练难度。
论文从观点立意，到网络架构的调整，参数的优化，是一个中规中矩的研发流程。