论文解读-《DiffWire Inductive Graph Rewiring via the Lovász Bound》
1. 论文介绍
论文题目:DiffWire: Inductive Graph Rewiring via the Lovász Bound
论文领域:图神经网络,图重连算法
论文发表:Learning on Graphs Conference 2022
论文背景:

2. 论文摘要
图神经网络(GNN)已被证明可以在处理与图相关的任务方面取得有竞争力的结果,例如节点和图分类、链接预测以及各种领域的节点和图聚类。大多数GNN使用消息传递框架,因此被称为MPNN。尽管它们的结果很有希望,但据报道,MPNNs存在过度平滑、过度挤压和伸展不足的问题。文献中提出了图重新布线和图池作为解决这些局限性的解决方案。然而,大多数最先进的图重布线方法无法保持图的全局拓扑结构,既不可微也不可归纳,并且需要调整超参数。在本文中,我们提出了DiffWire,这是一种利用Lovász界进行MPNN中图重连的新框架,具有原则性、完全可微性和无参数性。所提出的方法通过在MPNN中提出两个新的互补层为图重新布线提供了一个统一的理论:CT层,一个学习节点连接跳跃数并将其用作边重新加权的相关函数的层;GAP层,一个根据网络的性质和手头的任务优化频谱间隙的层。我们使用用于图分类的基准数据集分别实证验证了这些层的价值。我们还对CT层用于同质和异质节点分类任务进行了初步研究。DiffWire将节点连接跳跃数的可学习性与曲率的相关定义结合在一起,为创建更具表现力的MPNN打开了大门。
3. 相关介绍
3.1 背景介绍
有效解决图的过度挤压和过度平滑的问题,有图池化和图重连方法。
很多的图重连方法依赖于边采样策略,边会根据一个相关函数产生的权重来进行采样,边的相关性可以通过不同的方式计算,如随机,相似度,或者边的曲率等。
目前图重连方法的SOTA的采样策略有三个大的局限性:1,不能保留整个图的全局拓扑结构,2,大部分图重连方法既不可微也不可归纳,3,基于扩散度的相关函数是超参数配置的,无疑增加了一层复杂度。
图结构学习GSL:同时学习最优化的图结构和相关的特征。diffWire算法可以视为是GSL算法,CT-layer是一个基于度量的神经网络,GAP-layer是一个直接优化图结构的神经网络
3.2 本文的贡献
1,最重要的贡献是提出了一个理论框架DiffWire,是可微的,归纳式的,而且没有超参数限制。基于Lovasz边界;
Lovasz边界是一个把跳跃数和网络的谱间隙联系起来的边界,DiffWire可以预测最优图结构。目前研究领域的跳跃数和曲率,曲率和谱间隙之间的关系并没有一个统一的理论来描述。
我们的目标是把图扩散和曲率理论进行联系,给出一个新的图重连方法,能够保证图的结构。
2,使用CT作为一个相关性函数来进行边的重加权,由此产生一个CT layer作为GNN的一部分来学习CT;
3,使用GAP-layer来进行优化任务的谱间隙;
4,将CT layer和GAP-layer进行训练去获得CT处理后的特征和最小化图的谱间隙;
4. DiffWire算法
根据统一理论,给出两种新的层,CT层,学习跳跃数时间和作为相关性函数来进行边的重加权,GAP层,基于神经网络来优化谱间隙
整个算法的框架如下

4.1 Lovasz边界
Lovasz边界是图论和组合优化中的一个重要工具,用于分析图的各种性质,在谱图理论和图划分问题上有着重要的作用。改进后的Lovasz边界,在图分析和机器学习上更具有实用性,核心在于将图的拉普拉斯矩阵的特征值和图的几何性质(如有效阻尼)联系起来。
关于Lovasz边界有如下的不等式,该边界说明了图的任意两个节点的有效阻尼收敛到一定的范围。
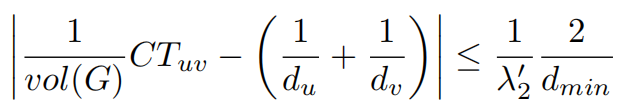
其中H_uv是从u节点到v节点所经历的期望跳跃次数,其中通勤时间(commute time)CT_uv=H_uv+H_vu,CT_uv是从u节点跳跃到v节点再返回到u节点的总的期望跳跃次数,也是两个节点的有效阻尼。vol(G)是图的体积volume,即图的所有节点的度的总和,d_u和d_v分别是节点u和v的度,d_min则整个图的最小的度。
其中谱间隙的定义为
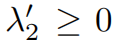
也是归一化拉普拉斯矩阵的第一个非零特征值
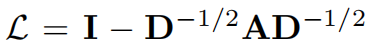
所以有:谱间隙越大,CT_uv/vol(G)就越接近1/d_u+1/d_v,因此通勤时间的信息含量就越少。
在图分类任务中,CT层,侧重于不等式左侧,当图的谱间隙较小的时候产生良好表现;GAP层,侧重于不等式右侧,当图的谱间隙较大的时候采用。
有效阻尼CT_uv可以看作是另一种节点u和v之间的相似度度量,用作节点相似性度量的优势
- 1, 全局视角。有效阻尼考虑了图中所有的可能的路径而不是最短路,期望跳跃步数。
- 2,鲁棒性:基于整个图的结构,对局部扰动和噪声有更好的鲁棒性
- 3,与谱特性的联系: 与图的拉普拉斯矩阵的特征值和特征向量直接关联
4.2 CT层
谱稀疏化和通勤时间的关系
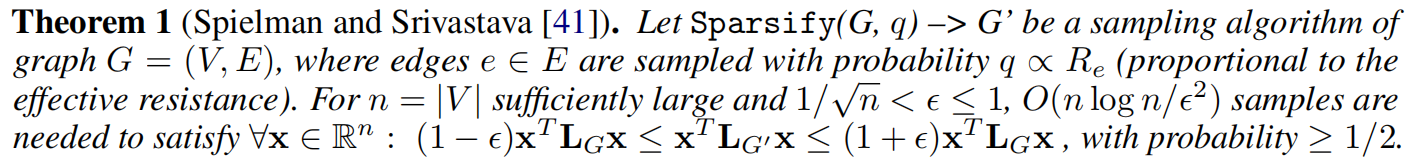
定理1可以用迪利克雷能量来简单解释,基于通勤时间的采用是一种保留图原始结构的同时对图进行重连的方法,受到迪利克雷能量限制。
通勤时间嵌入
通过神经网络的方式来学习,因为有效阻尼的计算方式可以由
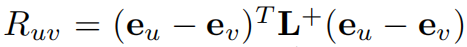
其中,e是单位向量,e_u是只有在u位置为1,其他为0的单位向量。
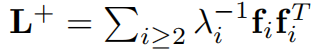
所以,通勤时间嵌入矩阵Z为
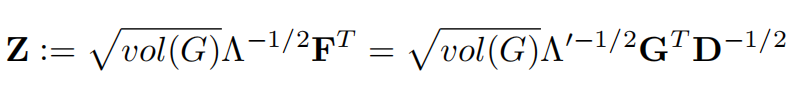
CT层的详细描述为
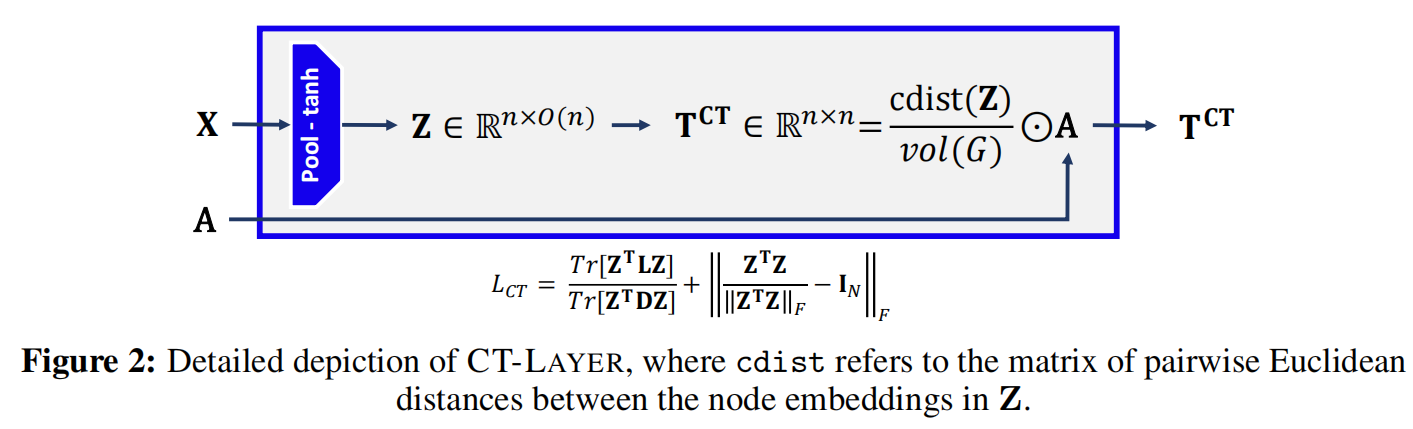
核心思想是学习节点之间的通勤时间,将其用作边缘重加权的相关函数。通勤时间是有效电阻的线性函数,因此CT-layer能够间接学习节点之间的有效阻尼关系。
CT层的工作原理:
- 1,学习通勤时间:通过神经网络学习节点之间的通勤时间,表示为节点特征的函数。
- 2,计算相关函数: 根据学习到的通勤时间来计算边的权重调整因子,作为边缘重加权的相关函数
- 3,边缘重加权: 使用计算得到的权重调整因子来调整原始图的边权重,生成新的加权图。
此外,CT层是完全可微的设计,那意味着可以将CT层之间作为神经网路一部分来参与训练
在同质图中节点倾向于相似节点相连,CT层会加强这种结构;在异质图中不同类型的节点倾向于相连,CT会调整边权重,连接特征空间相近但图结构距离远的节点
4.3 GAP层
Lovasz边界的不等式的右侧依赖于图的谱间隙,因此图谱间隙越大,通勤时间就越长,越接近无信息状态。
GAP层关注如何重新连接图的邻接矩阵A,以最小化图谱间隙。使用关于A的每个分量的梯度,即使用拉普拉斯矩阵或者归一化拉普拉斯矩阵来计算梯度。
使用比率割的近似来进行图重连
相关的梯度为
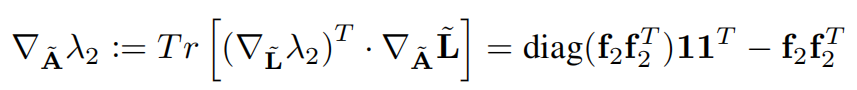
使用归一化割的近似来进行图重连
相关的梯度为
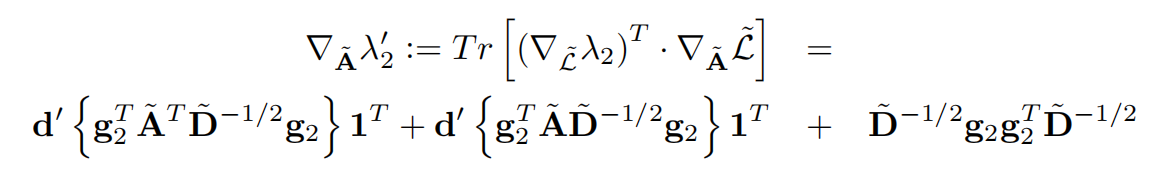
GAP层的详细描述

核心作用是优化图的谱间隙,基于改进后的lovasz边界理论,直接优化图的拉普拉斯的特征值。(最大化拉普拉斯矩阵的第二小的特征值)
GAP层的定义

面临的挑战:
- 1,非凸问题,谱间隙优化是一个非凸问题,存在多个局部的最优解
- 2,计算复杂度,特征值分解的计算复杂度较高
- 3,离散型:图重连操作的增减边是离散操作,难以持续优化
GAP层和CT层之间的协同作用
共同优化图的结构和谱特征,体现在几个方面
- 1,互补优化目标:CT层关注节点间的有效阻尼关系,GAP层关注全局的谱特性,两者实现局部和全局的平衡。
- 2,信息共享:CT层的有效阻尼信息给GAP层,更好优化谱间隙。
- 3,联合训练:共同形成端到端的整个训练架构
5. 实验设置
本文的实验主要是在图分类上,基线模式是MinCut
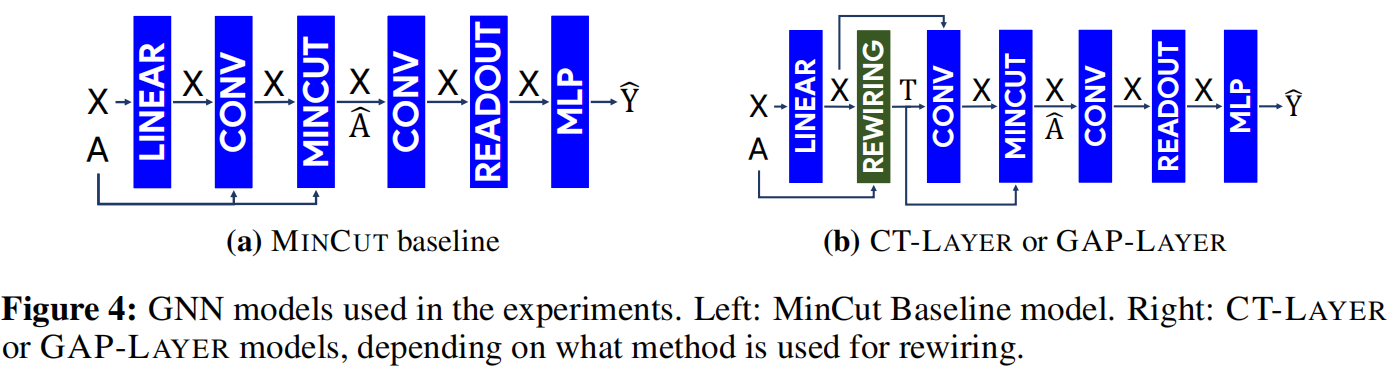
实验结果说明了CT层和GAP层在图分类任务上可以显著提高基线模型的表现。
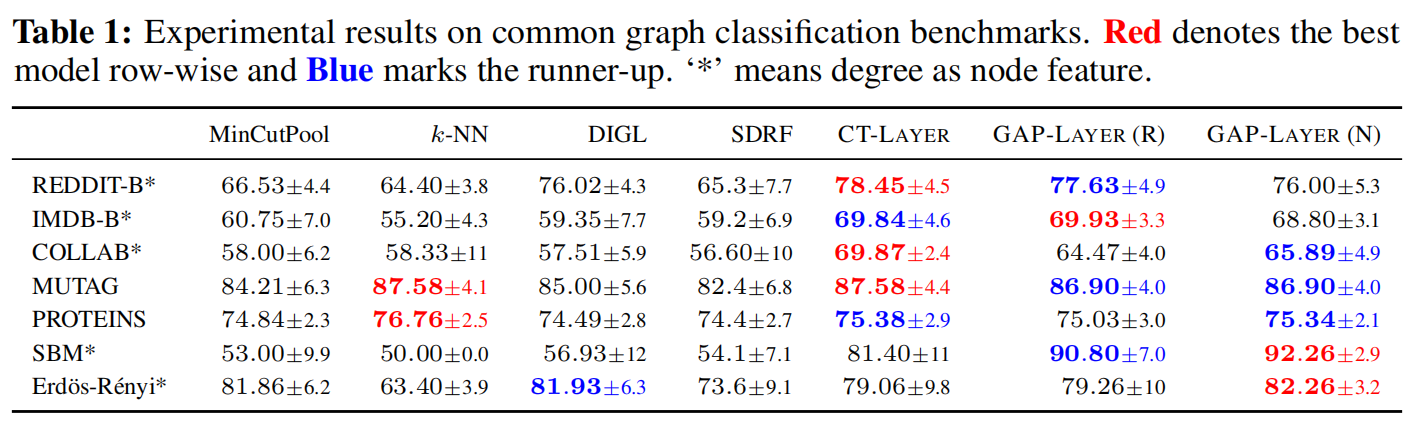
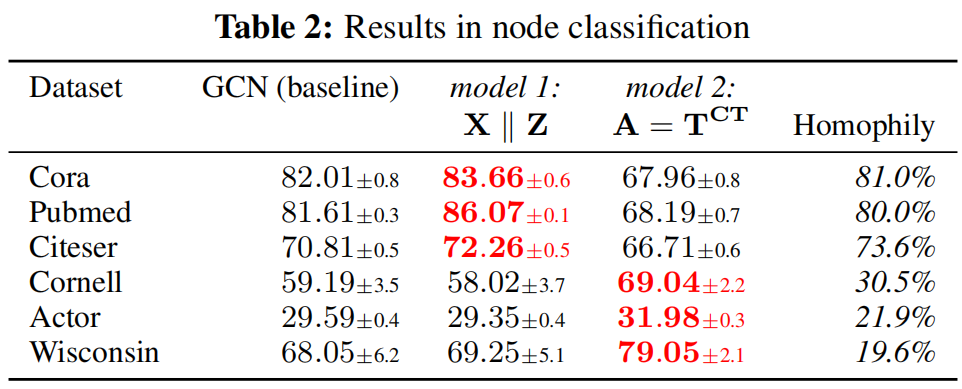
本文两层算法主要是针对图分类任务的表现而设计的,但同样在节点分类上由应用的潜力。
其中model1是在同构图中使用CTEs作为特征表现更好,model2是在异质图上使用 $T^{CT}$作为邻接矩阵的表现更好。
6. 总结和个人感悟
同时考虑局部和全局,局部依靠通勤时间,全局依靠谱间隙。来达成一个平衡。
总的来亮点是局部和全局性质的考虑。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号