论文解读-《Diffusion Improves Graph Learning》

1. 论文介绍

论文题目：Diffusion Improves Graph Learning
论文领域：图神经网络，图重连
论文发表：NeurIPS 2019
论文核心算法：DIGL
论文背景：

2. 论文摘要

图卷积是大多数图神经网络（GNN）的核心，通常通过直接（一跳）邻居之间的消息传递来近似。在这项工作中，我们通过引入一种强大但空间局部化的图卷积来消除仅使用直接邻居的限制：图扩散卷积（GDC）。GDC利用了广义图扩散，例如热核和个性化PageRank。它缓解了真实图中噪声和经常任意定义的边的问题。我们发现GDC与基于光谱的模型密切相关，因此结合了空间（消息传递）和光谱方法的优点。我们证明，用图扩散卷积代替消息传递，可以在监督和无监督任务以及各种数据集上的各种模型上持续显著提高性能。此外，GDC不仅限于GNN，而且可以轻松地与任何基于图的模型或算法（如谱聚类）相结合，而不需要对后者进行任何更改或影响其计算复杂性。我们的实施可以在网上获得。

3. 主要内容

由于消息传递神经网络仅利用直接邻域信息，因此常被称为空间方法。另一方面，基于频谱的模型不仅依赖单跳邻居，还能捕捉更复杂的图结构特性。为了调和这两种独立方法并融合其优势，我们提出了一种受谱方法启发的新型消息传递技术：GDC。

3.1 论文贡献

1，提出了GDC，一种更强大、更通用且空间局部化的替代方案，它采用稀疏化广义图扩散形式来替代消息传递机制
2，分析了GDC和图扩散的谱属性，展示了图扩展可以表示为等价的多项式滤波器，分析了GDC在图谱上的作用
3，比较和分析了GDC的多个变种，展示了其在图监督和图非监督学习上的应用

3.2 广义图扩散

通过扩散矩阵来定义一个广义上的图扩散

为了让S能够最终收敛，需要设置一些严格的条件，让所有的θ的和为1，T的特征值范围为[0,1]。

转移矩阵T包括随机游走转移矩阵和对称转移矩阵。
随机游走转移矩阵为

对称转移矩阵为

进一步通过加入自循环来调整随机游走矩阵

3.3 图扩散

两个常见的图扩散是PPR（Personalized PageRank）和热核，还有一种特殊的。
其中PPR的转移矩阵是随机游走矩阵，θ值是基于跳转概率的值

热核算法的转移矩阵是随机游走矩阵，θ的取值为

还有一种特别的图扩散算法

4. Graph Diffusion Convolution 图扩散卷积

算法架构图

发现GDC的过程，使用经过稀疏化的邻接矩阵依然在模型中有效，这就可以使用度校正随机分块模型来重连接图。所以GDC可以用于任何基于图的模型和算法

从GDC直觉来看，算法平滑了图的邻居，类似一种去除噪声的高斯滤波。PPR能够重建采样随机块模型（SBM）图的基础概率矩阵。

4.1 稀疏化

一般的图扩散都会形成一个稠密矩阵。然而矩阵S代表的是两节点之间的影响，是高度局部化的。相较于基于频谱的模型，这具有显著优势，因为频谱域无法提供任何局部性概念。空间定位特性使我们能够直接截断S矩阵中的较小数值并恢复稀疏性，从而得到矩阵S̃。
考虑了两种稀疏化方案：1. top-k方法：选取每列中块值最高的k个条目；2. 阈值方法：将低于设定阈值的条目置零。
需要注意的是，稀疏化预处理阶段仍需计算稠密矩阵S。但很多图扩散方法以近似计算而高效。
此外，top-k截断法会生成规则图，这种方法适用于批处理方法，并能解决与节点度数差异过大相关的问题。
最终经过稀疏化，转移矩阵可以写为

局限：
GDC是基于同质性图的假设。对于异质图，有一个方法扩展到GDC上是使用负边的权值。

4.2 GDC的谱分析

GDC是一个基于空间的方法，但是仍然可以被图谱领域的图卷积算子给解释。接下来主要分析GDC算法和基于谱的方法的联系，
图卷积可以定义为

为了让GDC的转移矩阵与θ，和多项式与ξ建立联系，有

上面的得到了，直接反映了图扩散和谱方法的联系。

由上面的置信度关联为

4.3 GDC的谱属性

我们现在将讨论范围扩展到GDC的所有部分，并分析它们如何改变图拉普拉斯算子的特征值。
GDC包含四个步骤：

• 1 ，计算转移矩阵T
• 2，根据图扩散公式和T来获得S
• 3，将S的小值截断进行稀疏化，来得到新的S
• 4，基于新的S来计算新的转移矩阵T。

对于转移矩阵，计算转移矩阵T仅改变我们用于分析图谱的拉普拉斯矩阵类型，一般使用对称转移矩阵或随机游走矩阵。

求和运算不会改变原矩阵的特征向量，因为对于矩阵T的特征向量vi及其对应特征值λi，有Tᵏvᵢ = λᵢTᵏ⁻¹vᵢ = λᵢᵏvᵢ。这也表明特征值会按此规律进行转换。

对于PPR是

对于热核是

PPR（个性化PageRank）与热核都充当着低通滤波器的角色。对应于图中大规模结构的低特征值被放大，而对应于精细细节但同时也包含噪音的高特征值则被抑制。

4.4 稀疏化的分析

因为稀疏化会改变其特征值和特征向量，无法直接建立联系。所以使用特征值扰动理论

实验发现，稀疏化的微小改动影响最大的是最大的和最小的特征值。

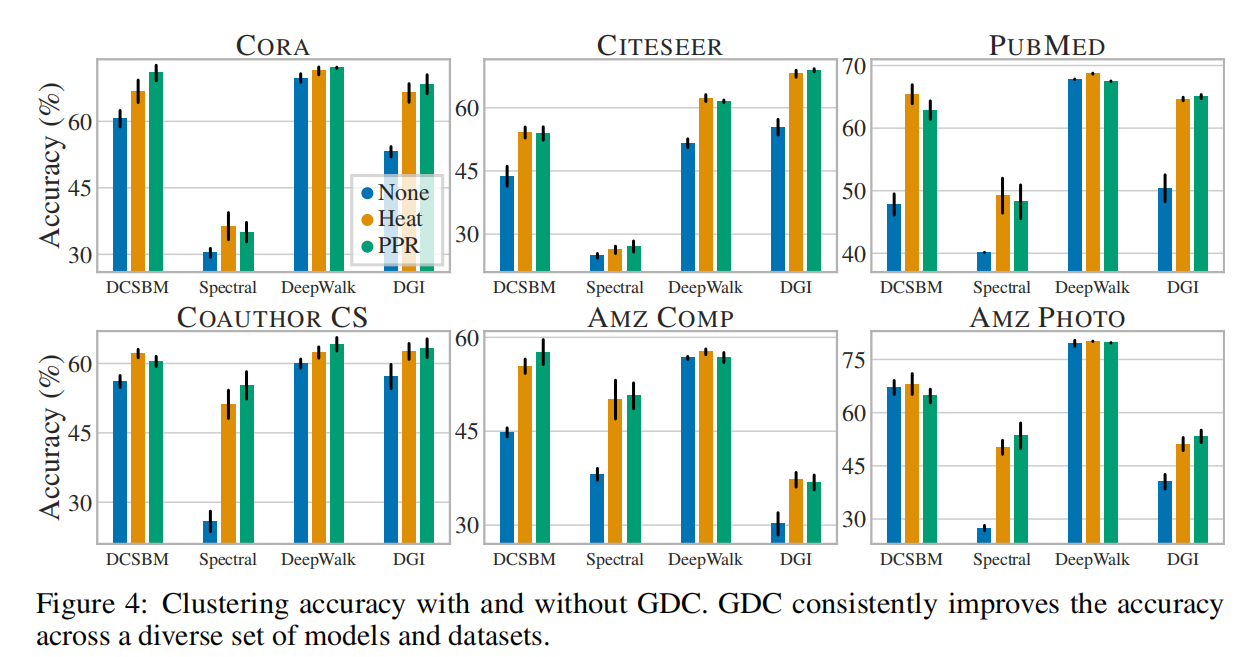
5. 实验设置

数据集选择6个：文献引用网络citeseer，cora，pubmed，co-author CS，AMAZON COMPUTERS 和 AMAZON PHOTO。
将GDC使用在9个模型上，监督模型有 GCN，GAT，JK，GIN，ARMA。非监督模型有：DCSBM，谱聚类，DeepWalk，和DGI。

6. GDC算法Python代码

整个算法就一个函数可以实现

def gdc(A: sp.csr_matrix, alpha: float, eps: float):
    N = A.shape[0]
    # Self-loops
    A_loop = sp.eye(N) + A # A_loop = I + A

    # 2. 构建对称归一化的转移矩阵 T_sym = D^(-1/2) * (A+I) * D^(-1/2)
    # 这一步将邻接矩阵转换为概率转移矩阵，使信息能够在图上平滑传播
    D_loop_vec = A_loop.sum(0).A1  # 计算每个节点的度（行和）
    D_loop_vec_invsqrt = 1 / np.sqrt(D_loop_vec)  # 计算度的平方根的倒数
    D_loop_invsqrt = sp.diags(D_loop_vec_invsqrt)  # 构建对角矩阵 D^(-1/2)
    T_sym = D_loop_invsqrt @ A_loop @ D_loop_invsqrt  # 对称归一化

    # 3. 基于PPR的扩散：计算无限级数 S = α(I - (1-α)T_sym)^(-1)
    # 这是一个递归过程，表示从每个节点出发，以概率 α 停留在当前节点，或以概率 (1-α) 转移到邻居
    S = alpha * sp.linalg.inv(sp.eye(N) - (1 - alpha) * T_sym)  # 解析解形式的PPR矩阵

    # 4. 稀疏化处理：移除权重小于阈值 eps 的边，降低计算复杂度
    S_tilde = S.multiply(S >= eps)  # 保留 >= eps 的元素，其余置零
    
    # 5. 列归一化：将稀疏化后的矩阵转换为列随机矩阵（每列和为1）
    # 这使得矩阵可以作为转移概率矩阵使用
    D_tilde_vec = S_tilde.sum(0).A1  # 计算稀疏化矩阵的列和
    T_S = S_tilde / D_tilde_vec  # 列归一化：T_S = S_tilde * D_tilde^(-1)
    
    return T_S

7. 总结和个人感悟

图扩撒领域的经典，重点是作者引用稀疏化扩散方法，该空间上的方法和谱域相关方法的等效。