论文解读-《Understanding over-squashing and bottlenecks on graphs via curvature》

1. 论文介绍

论文题目：Understanding over-squashing and bottlenecks on graphs via curvature
论文核心算法：SDRF
论文领域：图神经网络
论文发表：outstanding paper honorable mention at ICLR 2022
论文背景：

2. 论文摘要

大多数图神经网络（GNN）使用消息传递范式，其中节点特征在输入图上传播。最近的工作指出，来自远程节点的信息流失真是限制依赖于长距离交互的任务的消息传递效率的一个因素。这种现象被称为“过度压缩”，被启发式地归因于图瓶颈，其中k跳邻居的数量随着k值的快速增长。我们对GNN中的过度压缩现象进行了精确的描述，并分析了它是如何从图中的瓶颈中产生的。为此，我们引入了一种新的基于边的组合曲率，并证明了负弯曲边是导致过度挤压问题的原因。我们还提出并实验测试了一种基于曲率的图重布线方法来缓解过度挤压。

3. 相关工作

过度平滑的问题已经有研究，过度挤压的问题还没有良好解决方案，目前已有的图重连方案，通过减少图的瓶颈来缓解。但是关于过度挤压和拓扑结构的瓶颈问题的关系还是没有清晰的描述。
我们使用流形领域（局部具备欧几里得空间性质的拓扑空间）的微分几何来描述过度挤压问题。本文的理论为研究图的性质提供了一个引人入胜的框架，特别指出图与流形类似，具有使其更适宜在双曲几何空间中实现的曲率特征。

3.1 本文贡献

首个从几何角度来研究消息传递神经网络中的图瓶颈现象和过度挤压问题

3.2 过度挤压问题的分析

对于消息传递神经网络MPNN，在此我们采用增广归一化邻接矩阵来实现节点间信息传递，该方法直接导致消息函数ψ的度归一化处理。
若存在长程依赖关系，来自非相邻节点的信息需在网络中传播而不被过度扭曲。但是在很多情况下，邻居感受野的范围尺寸会以r层数的方式指数级增长，邻居节点的指数增长的信息也会被压缩到固定尺寸的特征，这就发生了过度挤压现象。

3.3 使用雅可比矩阵来进行分析

只要更新函数和消息聚合函数是可微的，那么第l层隐藏层的特征h对于输入特征x就是一个可微函数。那么信息过度压缩现象可以理解为：当节点i的表示h(i)无法受到与其相距r的节点s的输入特征x_s影响时发生的情况。
有引理1，雅可比矩阵的边界为

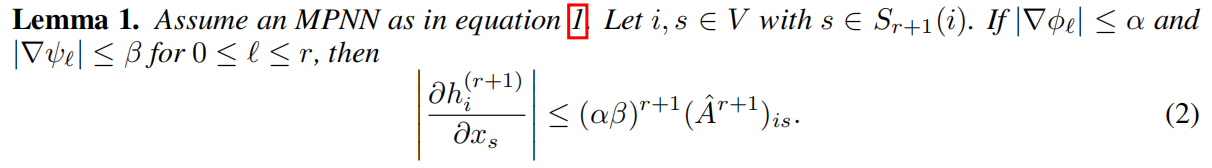
引理给出通过节点特征的雅可比因子来衡量过度挤压问题。

3.4 图曲率和图瓶颈

黎曼几何中的一个自然对象是里奇曲率，这是一个双线性形式，用于确定测地线的分散性，即从具有"相同"速度的邻近点出发的测地线是保持平行（欧几里得空间）、收敛（球面空间）还是发散（双曲空间）。
节点的连接关系主要有三种情况

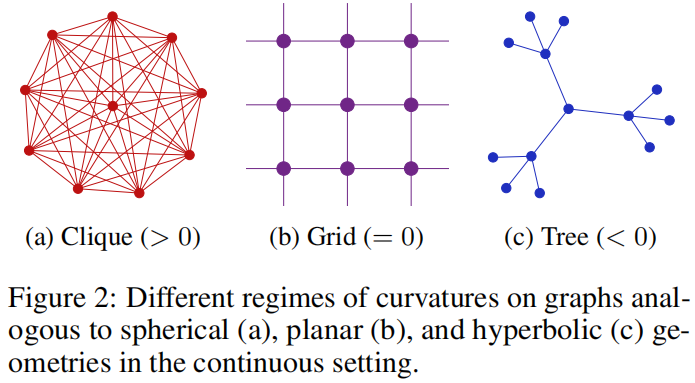
基于边的曲率主要有两类，Forman曲率和Ollivier 曲率，本文提出了一种新的曲率。
平衡福尔曼曲率定义为：

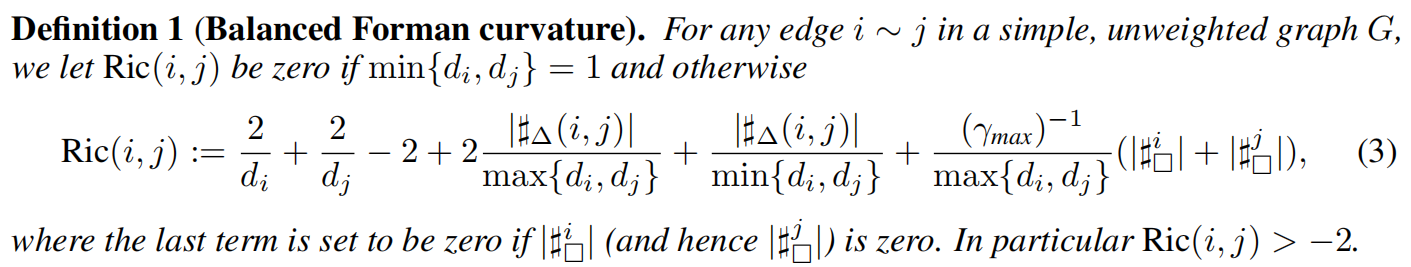
有引理

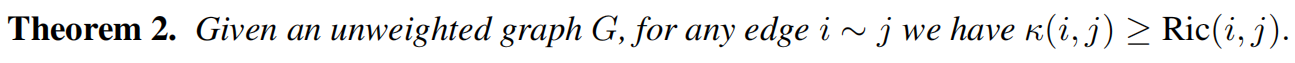
所以有

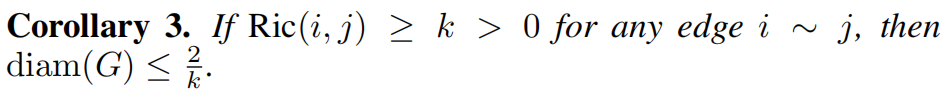
根据上面的分析，建立了局部曲率和雅可比值的关系。那接下来需要证明的是：具有高负曲率的边正是导致图结构瓶颈并引发过度挤压现象的元凶。

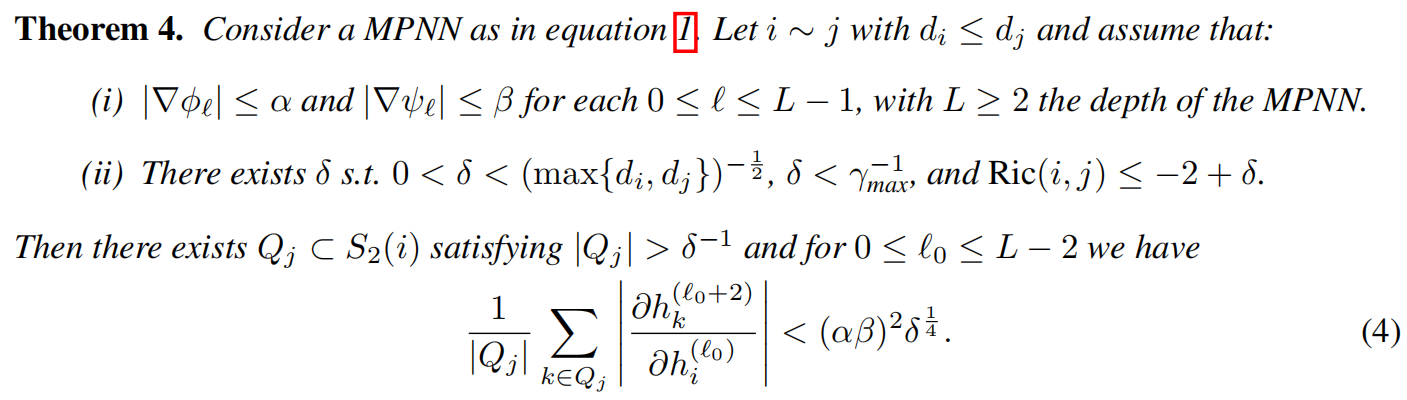
条件1总是成立的，这使我们能够控制消息传递函数。
定理4表明，若存在如情形(ii)所述的负曲率边，则存在大量节点k，使得图神经网络平均而言难以在两层内将信息从i传播至k——尽管这些节点k与i的间距仅为2。
在这种情况下，过压缩现象通过方程4中的雅可比行列式测得，从而导致信息传播受阻。若当前任务涉及长程依赖关系，那么由负曲率边引发的过压缩效应可能会影响模型性能。

3.5 通过Cheeger常量限制的瓶颈

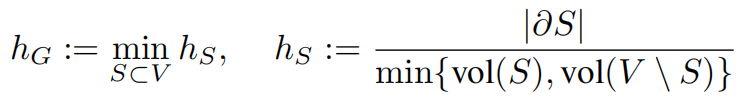
所以有Cheeger不等式

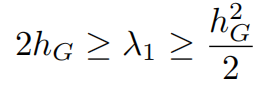
由于定理4表明负曲率边会导致瓶颈效应，我们预期hG与图的曲率之间存在关联。

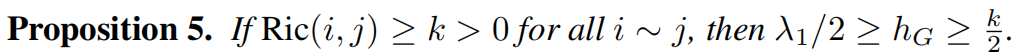
曲率存在正下界使我们能够控制hG，从而控制该图的谱隙

4. 基于曲率的图重连方法

最近出现了一种趋势，即将输入图与用于信息传播的图进行解耦。这可以采取图子采样或重采样的形式来处理可扩展性问题或拓扑噪声，使用更大的基于基序或多跳滤波器，或者将图改变作为预处理步骤或为下游任务进行自适应调整。
我们还严格证明，基于随机游走的重新布线方法通常可能无法获得边集，该边集在切赫常数衡量的瓶颈性方面有显著改善。
一种基于曲率的重新布线方法应着力缓解图中强负曲边。为此，我们实施了一种名为"随机离散里奇流"(SDRF)的简单重布线方法

算法伪代码

在每一次迭代中，给图添加上最负曲率的边，移除掉最为正曲率的边。
该方法受到连续（逆向）里奇流的启发，旨在使边缘曲率均匀化。这与图结构上里奇流的直接扩展不同——在那些方法中，跨负曲率边缘传播信息会变得越来越耗费计算资源。

GNN的曲率示意图

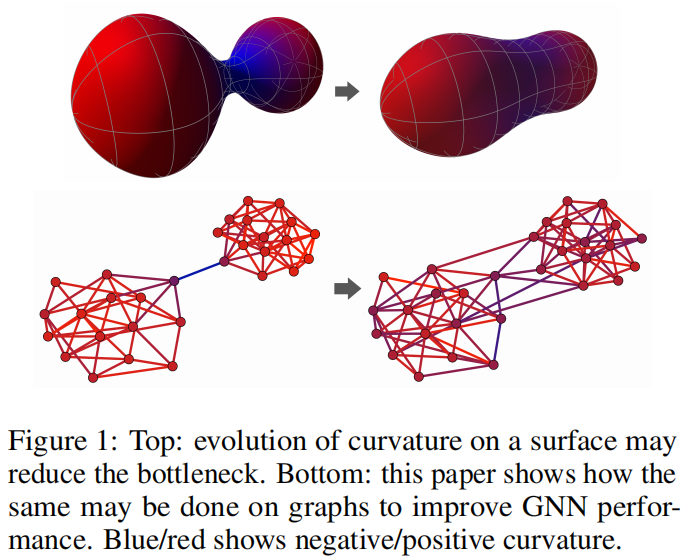
基于随机游走的图重连可以解决图瓶颈吗？
比较好理解SDRF的方法是对比基于随机游走的图重连算法和SDRF方法。
假设我们给定一个具有较小h(G)值的图G，希望通过重新布线将其改造成图G0，使其切比雪夫常数显著改善，从而缓解节点群间的瓶颈效应。
一种基于随机游走的重新布线方法，如DIGL，其作用是通过平滑图邻接关系，从而倾向于促进短距离节点之间的连接。这种方法不能很好解决结构瓶颈，而是在那些处于长扩散距离的节点上反而更为显著。
考虑一个经典的例子，PPR（Personal Page Rank）矩阵的定义为

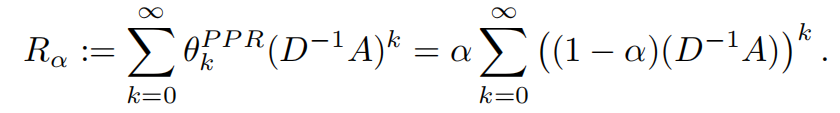
那么，基于R来进行图重连后，新的Cheeger常量的计算方式为

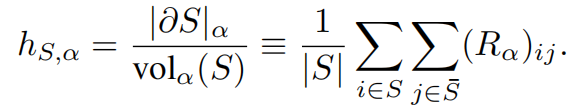
基于此，很难去提高该值。

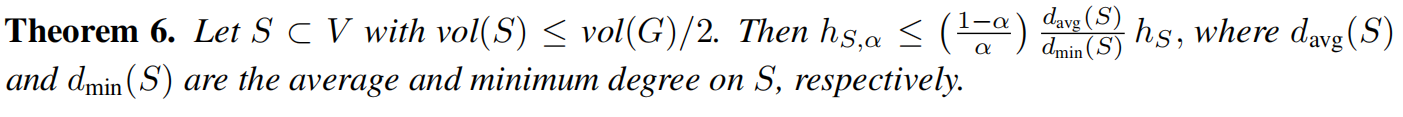
新型Cheeger常数直接受旧常数控制的特性源于这样一个事实：类似Klicpera等人(2019年)采用的随机游走方法，其设计初衷是对社群内部边而非社群间边产生更显著影响，因为该方法优先考虑短扩散距离节点。
定理6暗示着像DIGL这样的扩散方法可能无法产生具有充分改善瓶颈的新边集E0。

更好的保存图结构，算法针对的是最大负曲率的边。
SDRF修改的边一般是有最大负曲率样本的，而这样样本一般是高度节点。对高度节点的修改，让度的分布可以更好的保存。同时GCN对高度节点的扰动更有稳定性。

同质性和图瓶颈
虽然目前的图重连算法都是基于图的拓扑结构而不考虑节点的同构和异构。DIGL方法是提高图中基于短扩散距离的节点的连通性。对于一些同质数据来说，有着短扩散距离的节点一般更可能是不同标签，DIGL就给数据引入了噪声。
SDRF是主要关注最负曲率的边，在不显著增加不同标签节点间连接性的情况下减小了瓶颈。

5. 实验设置

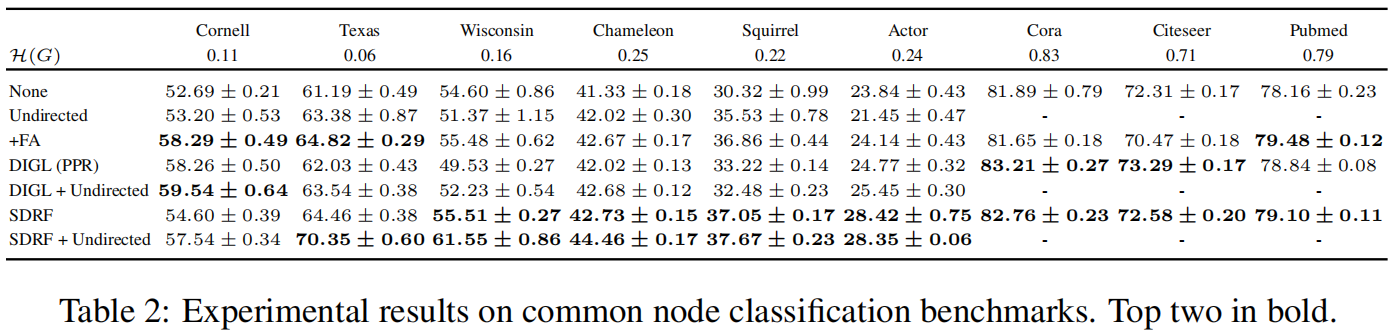
对比方法有DIGL 和 +FA方法
实验数据为，节点分类任务SDRF表现最好。

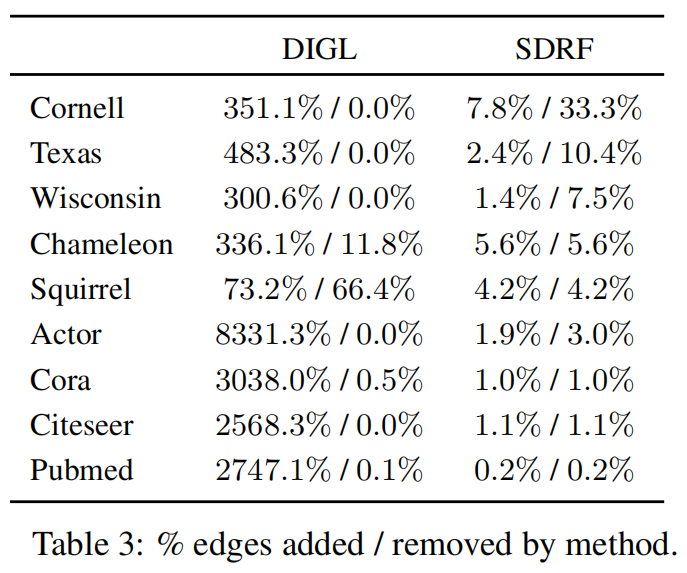
图拓扑改变
SDRF可以尽可能保存原始的图拓扑结构

6. 总结和个人感悟

理论证明了图瓶颈造成了图过度挤压的根源，证明了图重连方法关注解决图瓶颈即可，而图瓶颈是由于最负面曲率节点来决定的，最终的工作是添加最负曲率的边即可。
论文的理论分析太多。整体上不是很懂，后续有时间再来读