论文解读-《Revisiting Over-smoothing and Over-squashing Using Ollivier-Ricci Curvature》
1. 论文介绍
论文题目:Revisiting Over-smoothing and Over-squashing Using Ollivier-Ricci Curvature
论文领域:图神经网络
论文发表:ICML 2023
论文代码:https://github.com/hieubkvn123/revisiting-gnn-curvature
论文背景:

2. 论文摘要
图形神经网络(GNN)已被证明在本质上容易受到过平滑和过挤压问题的影响。这些问题限制了GNN在考虑远距离信息时的有效性,从而限制了其对复杂图形交互进行建模的能力。我们的研究揭示了局部图几何与这两个问题的发生之间的关键联系,从而为使用Ollivier Ricci曲率在局部尺度上研究它们提供了一个统一的框架。具体地,我们证明了过度平滑与正图曲率相关联,而过度挤压与负图曲率相联系。基于我们的理论,我们提出了Batch Ollivier Ricci Flow算法,这是一种新的重新连线算法,能够同时解决过平滑和过挤压问题。
3. 相关介绍
GNN存在过度平滑问题,在更深层的节点的特征变得难以区分;
GNN受到过度挤压的限制,当消息传播被特征维度的瓶颈阻碍时会发生过度压缩,从而压缩远距离的消息。
现有方案通过孤立解决过度平滑和过度挤压的问题,缺乏统一的理论解释。
3.1 本文的贡献
- 1,证明了非常弯曲的OR边会导致节点表示变得相似,从而建立了过度平滑问题与高OR边曲率之间的联系。
- 2,证明了低OR边的值决定了整个图传递消息的瓶颈,也揭示了过度挤压问题和负OR边曲率的联系。
- 3,基于本文的理论结果,提出了BORF算法,一个全新的基于边曲率来重连的方法,同时来缓解过度平滑和过度挤压问题
3.2 相关工作
MPNN消息传递网络
节点u在K层的特征表示为X,那么一个通用的表达公式为

其中ψ是第K层的消息函数,⊕是聚合函数,ϕ是更新函数。那么针对不同结构的GNN,有

3.3 过度平滑的问题
当GNN的层数增加,任意两个邻居节点u和v的特征会趋向一致。公式可以写为
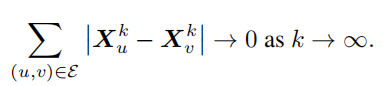
节点发生过度平滑的效果图如下

3.4 过度挤压问题
公式(1)展示的是信息在每层只传递节点间为1的距离,层的数量就是每个节点的接受域的大小。
随着层数增加,每一个节点的视野域呈现指数级增加。这导致呈指数级增长的远距离顶点之间的信息被压缩成固定大小的向量,从而限制了模型捕捉长程依赖关系的能力。
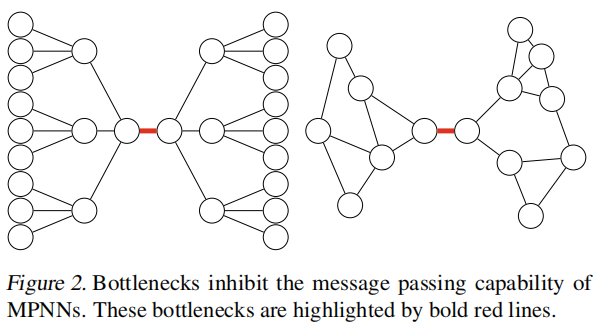
4. Ollivier-Ricci曲率
Ricci曲率是微分几何领域内常见的几何概念。在黎曼流形的局部邻域,空间的Ricci曲率表征了平均测地线色散,即附近点的给定方向上的直线路径是否有保持平行(零曲率)、收敛(正曲率)或发散(负曲率)的趋势。至关重要的是,里奇曲率的定义取决于在所考虑的空间内指定方向或更精确地说切线向量的能力。
4.1 Ollivier-Ricci介绍
为规避图上缺乏切线结构的局限,Ollivier-Ricci通过考察邻近点的随机游走来实现。
定义µ为从起步于v点到结束于P点的随机游走的概率。Π(µu, µv)是两者的联合概率分布。W1 表示这些分布之间的L1 Wasserstein距离。
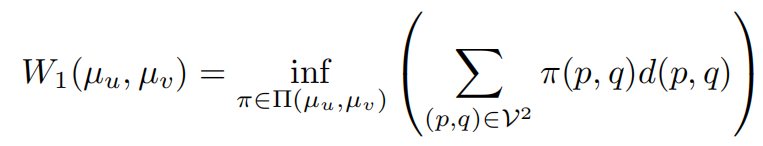
这个变量衡量了从u到v的随机游走的最小变量。
定义Ollivier-Ricci曲率k为
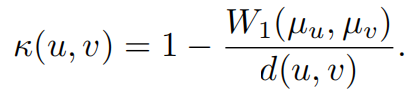
其中d表示的是原始距离。如果k为0,那么表示随机游走在一个平衡的距离,如果小于0,那是发散的,大于0则为收敛。
从直观来看,两个节点的共同邻居越多,则为正曲率,否则为负。
当k的定义完成,其中W1是一个需要优化的值,在线性优化中的优化函数为

图曲率的分析
对于u和v,假设deg(u)=n, deg(v)=m,n>m,那么有
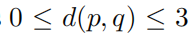
所以有
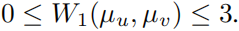
对于k可以有边界:

在不同的邻居节点下的k值的示意图
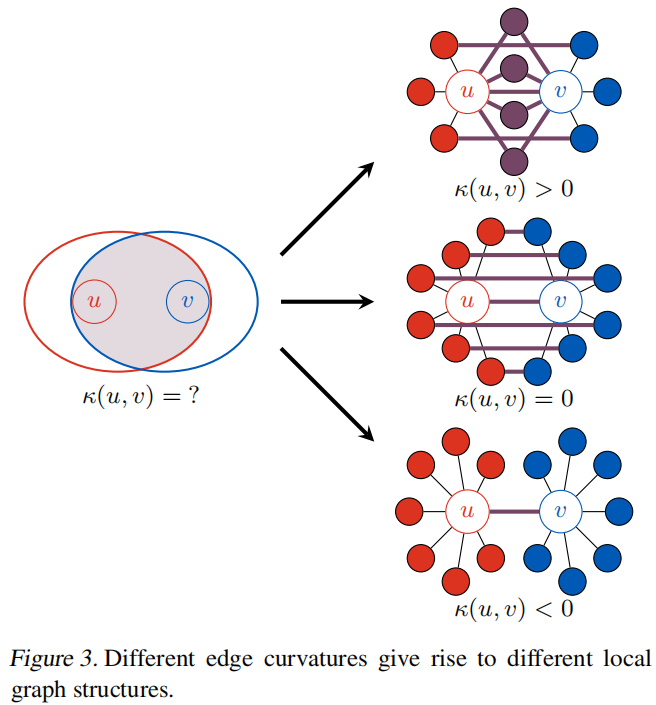
4.2 正曲率和过度平滑的联系
根据不等式,曲率K是u和v的共同邻居的部分的下边界。
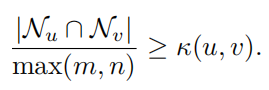
具有高度重叠邻域的节点聚合了几乎相同的信息,导致特征同质化。
有定理4.2 对于具有非常正曲率的边会强制相邻节点特征变得相似。

如果整个图都是正曲率,那么所有节点的特征会很快收敛到可区分的表征。这就解释了浅层GNN的过度平滑是由于正的曲率导致的。
对于任何的u和v有该不等式
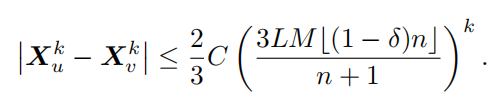
过度平滑问题的可以被C1, C2>0 的限制下
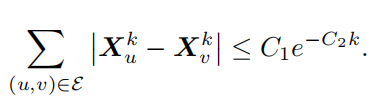
4.3 负曲率和过度挤压问题
局部图的瓶颈的出现,会导致负曲率的出现,因此出现过度挤压的问题。
通过瓶颈分析来建立,负的曲率说明了阻碍消息传递的结构性瓶颈

5. BORF算法
理论分析了过度平滑问题一般出现在大量的节点有高正曲率,过度挤压问题一般出现在大量的节点有高负曲率。
BORF算法简述,批次计算,每一批次进行三步:
- 第一步,先扎到最小曲率的h条边和最大曲率的k条边
- 第二步,通过向h条最小弯曲边的集合添加连接,来统一缓解图瓶颈问题。选取方法的目标是为了最小化消息传递消耗,整个图的消息传递成本为W1
![borfgnn22]()
那么,选择连边的p和q两个点的函数为
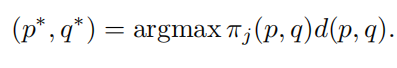
- 第三步,移除k条最大曲率的边
该算法还可以基于数据特点,对数据进行单纯的增加边,单纯的减去边,或者重置图的连边。
算法流程

其他的图重连算法
SDRF 基于边缘度量平衡福尔曼曲率(BFC),该曲率实际上是Olliver-Ricci曲率的下界
从根本上说,SDRF算法通过迭代方式寻找具有最低BFC的边,计算每条可能新增边对BFC造成的变化量,最终选择对前述边的BFC影响最大的那条边进行添加。
FoSR FoSR基于启发式方法,认为谱间隙能表征图的连通性。
在每一次迭代中,该算法会估算哪条缺失的边能最大程度改善谱间隙,并将该边加入图中。
6. 实验设置
使用于广泛应用的节点分类和图分类任务。
节点分类:Cora,Citeseer,texas,Cornell,WISCONSIN,Chameleon
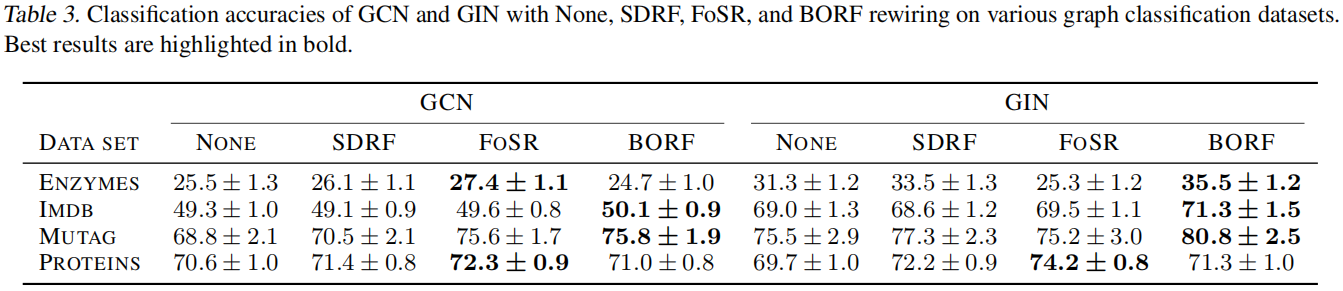
图分类: ENZYMES, IMDB, MUTAG, PROTEINS
基线模型是在GCN和GIN上进行
在节点分类上,BORF取得了最好的效果
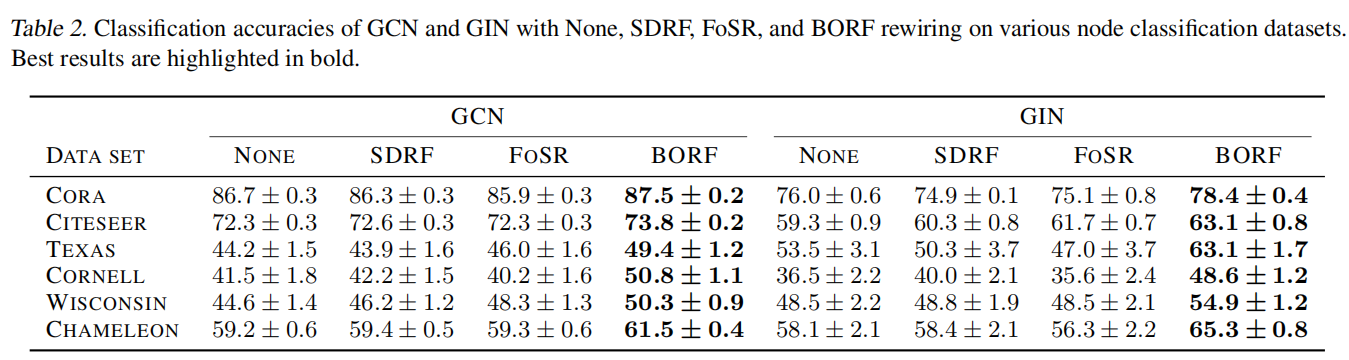
在图分类任务上,BORF也取得较好的效果
7. 核心代码
计算单条边的ricci曲率的核心代码
def _compute_ricci_curvature_single_edge(source, target):
"""Ricci curvature computation for a given single edge.
Parameters
----------
source : int
Source node index in Networkit graph `_Gk`.
target : int
Target node index in Networkit graph `_Gk`.
Returns
-------
result : dict[(int,int), float]
The Ricci curvature of given edge in dict format. E.g.: {(node1, node2): ricciCurvature}
"""
assert source != target, "Self loop is not allowed." # to prevent self loop
# If the weight of edge is too small, return 0 instead.
if _Gk.weight(source, target) < EPSILON:
logger.trace("Zero weight edge detected for edge (%s,%s), return Ricci Curvature as 0 instead." %
(source, target))
return {(source, target): 0}
# compute transportation distance
m = 1 # assign an initial cost
assert _method in ["OTD", "ATD", "Sinkhorn", "OTDSinkhornMix"], \
'Method %s not found, support method:["OTD", "ATD", "Sinkhorn", "OTDSinkhornMix]' % _method
x, y, neighbors_x, neighbors_y, d = _distribute_densities(source, target)
optimal_plan = ot.emd(x, y, d)
optimal_cost = optimal_plan * d
optimal_total_cost = np.sum(optimal_cost)
optimal_cost = pd.DataFrame(optimal_cost, columns=neighbors_y, index=neighbors_x)
# compute Ricci curvature: k=1-(m_{x,y})/d(x,y)
result = 1 - (optimal_total_cost / _Gk.weight(source, target)) # Divided by the length of d(i, j)
logger.debug("Ricci curvature (%s,%s) = %f" % (source, target, result))
return {
(source, target): {
'rc_curvature' : result,
'rc_transport_cost' : optimal_cost,
}
}
8. 结论
作者针对过度挤压和过度平滑的问题,给出了理论分析,基于该理论引出了对应的解决算法。理论证明+实验效果证明了其算法的有效性。



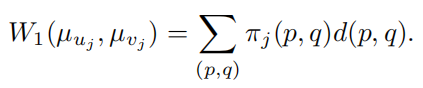

 浙公网安备 33010602011771号
浙公网安备 33010602011771号