论文解读-《Disentangled Graph Spectral Domain Adaptation》

1. 论文介绍

论文题目：Disentangled Graph Spectral Domain Adaptation
论文发表：ICML 2025
论文领域：图神经网络，非监督域适应，迁移学习
论文背景：

2. 论文摘要

分布转移和标签的缺乏阻止了图学习方法，特别是图神经网络（GNNs）的跨域推广。与嵌入对齐的无监督图域自适应（UDA）相比，无监督图域自适应（UGDA）由于表示中的属性和拓扑耦合而变得更具挑战性。除了嵌入对齐，UGDA转向拓扑对齐，但受所采用的拓扑模型和伪标签估计能力的限制。为了缓解这一问题，本文提出了一种解耦合图谱域自适应算法（DGSDA），该算法通过解耦合属性和拓扑对齐，并直接对齐拓扑之外的灵活图谱滤波器。具体地说，Bernstein多项式逼近在很大程度上模拟了待逼近函数的行为，用于捕捉复杂的拓扑特征，避免了昂贵的特征值分解。理论分析揭示了DGSDA的紧GDA界和多项式系数正则化的合理性。定量和定性实验验证了该算法的优越性。

3. 相关工作

传统的域自适应算法，使用中间的特征表达来最小化跨域的差异，可以分为两类：一类方法是最小化预定义的概率差别度量，另一类是使用对抗性学习技术。目前很多的域自适应算法都有着传统的局限性，主要解决特征级偏移而忽视结构的偏移。

对于解决图的结构自适应策略的领域有，StruRW算法通过边重新分配权重的机制来减缓跨域的条件邻居分布。PariAlign算法引入一种双自适应框架，通过自适应边调节权重同时重新校准节点的影响，并通过分类损失重新加权来抵消标签分布不匹配。

4. 论文贡献

论文的贡献可以总结为四点

• 1，提出了一个新的UGDA（非监督图域自适应）方法，解耦合属性和拓扑对齐，使用模型对齐来替换拓扑对齐
• 2，提出了一个新的DGSDA（解耦合的图谱域自适应）方法，通过直接对齐谱滤波器来实现，DGSDA是一个end-to-end，参数高效，能够处理高阶表达信息。
• 3，通过Bernstein多项式来分析了DGSDA的紧GDA界，和对对齐损失函数的调整。
• 4，用实验证明了UGSDA方法可以取得了一个新的SOTA

5. DGSDA介绍

特征向量空间对齐，是UDA非监督域自适应领域广泛采用的手段。拓扑结构模型的能力和伪标签样本的预估的准确度，决定了拓扑对齐的质量。

为了解决这个问题，本文提出了DGSDA解耦合图谱域自适应算法（Disentangled Graph Spectral Domain adaptation），将属性和拓扑结构对齐进行解耦合。

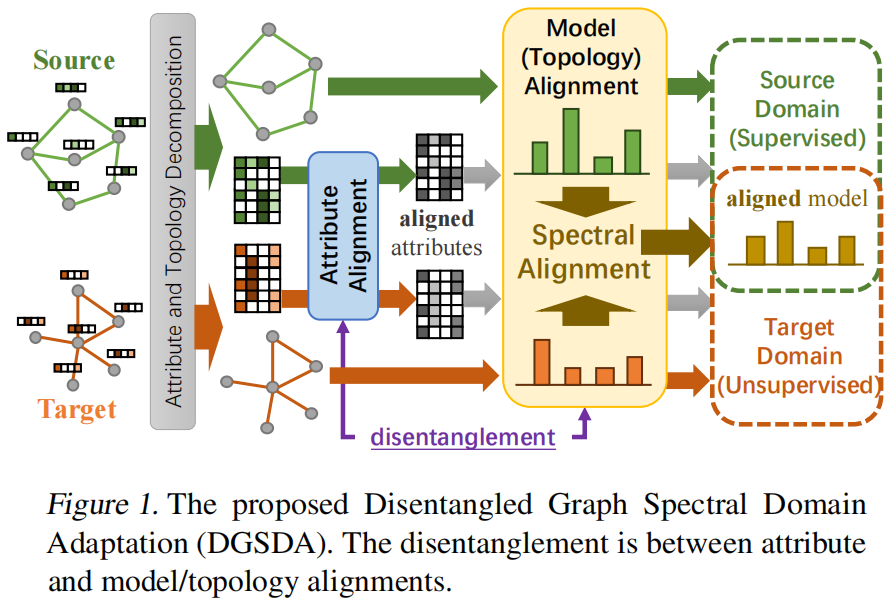
DGSDA分为两个部分来详细说明，分布偏移去耦合，图谱域自适应。

5.1 分布偏移去耦合

UGDA的目标是让特征空间分布对齐。图域自适应过程包括两个步骤：节点属性对齐，和拓扑对齐。
特征空间的对齐的目标是实现下列的相等
$$ P^S(H|Y) = P^T(H|Y) $$
因为有贝叶斯公式
$$ P(A, X|Y) = P(X|Y) P(A|X,Y) $$
所以在这里需要去处理，使用特征提取器来处理两者不相等的问题
$$ P^S(A,X|Y) \neq P^T(A, X|Y) $$
假如节点可以对齐，那么拓扑对齐问题从上面的公式，转换为
$$ P^S(A|X, Y) \neq P^T(A|X, Y) $$
最终可以把公式转为下，解决A的数据偏移的场景
$$ P^S(A|H_X, Y) \neq P^T(A|H_X, Y) $$

5.2 图谱域自适应

可以从实现GNN的对齐而不是拓扑对齐。
以谱GNN为例，图拓扑以其拉普拉斯矩阵的特征向量为U确定滤波数据的谱空间，U的定义在如下式子中。

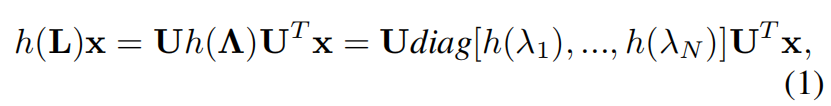
将GNN在多个领域内进行对齐，等同于拓扑结构的对齐。

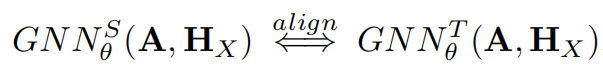
这样处理有三个好处

• 1，端到端的模型对齐，是拓扑对齐的最优。模型对齐等同于拓扑对齐+选择合适的GNN。相反，拓扑对齐也需要需要额外的GNN
• 2，模型对齐，为参数对齐，会更加有效。相比于边的计数，模型参数会更小和更独立
• 3，GNN的类型数量很多，相反，拓扑结构模型的数量很少

5.3 谱滤波对齐

由于拉普拉斯矩阵的特征值分解，最简单的谱GNN的计算开销很大。采用BernNet，其简单，高效，且理论支持学习任意的图谱滤波器。
t在[0, 1]的K阶Bernstein多项式近似为：

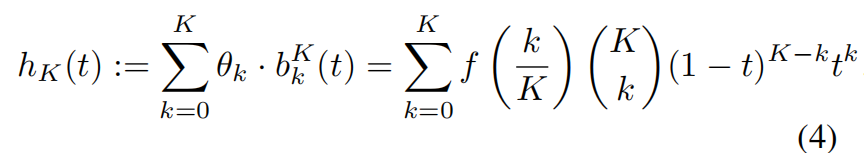
其中b为k阶Bernstein基

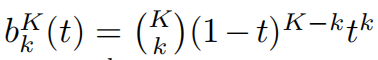
根据公式（1），那么对于谱域GNN在x的信号可以写为：

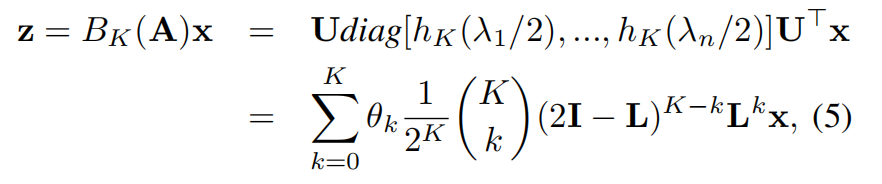
BernNet的好处：

• 1 ，z可以近似任意连续的滤波器
• 2，不需要高消耗的特征分解
• 3，BernNet可以通过指定θk精确地实现了GNN中常用的现有滤波器，例如线性/脉冲低通滤波器、线性/脉冲高通滤波器和脉冲带通滤波器。直观地，基（2I−L）=I+A和L分别对应于平滑和锐化操作。

GNN对齐的损失函数为：

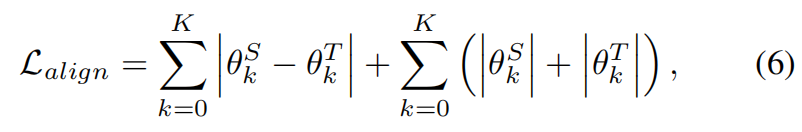
整个DGSDA的损失函数如下，包含四个部分，源域编码器，目标域编码器，节点属性对齐，模型对齐。

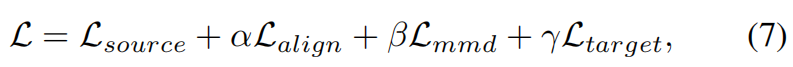
6. 理论分析

本节来分析域自适应的边界。

首先来看看Lipschitz连续的定义，

根据Lipschitz连续的定义，图数据的DA边界可以表达为

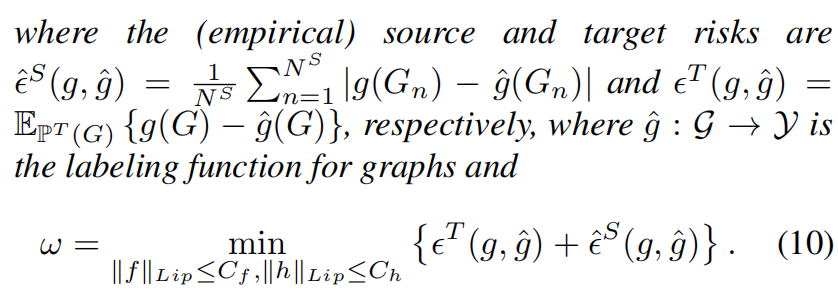
融入K阶的BernNet由：

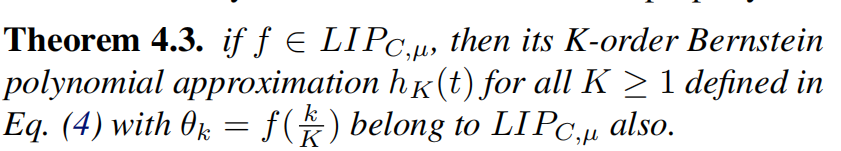
然后有：

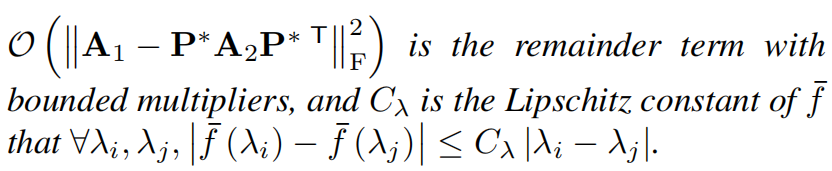
可以得到边界的上下界。

7. 实验设置

数据集：来自三个类型的benchmark数据集，引用网络，社交网络和交通系统的数据。
索引引用网络数据集：ArnetMiner（A），Citationv1（C）和 DBLPv7 （D）。
社交网络数据集：Catalog 和 twitch-DE/EN
交通系统数据集：Ariport-Brazil（B），Europe（E）和USA（U）。

基线：（1）只有源数据的方法；（2）使用节点空间特征向量来解决图域自适应问题，（3）适用于图结构偏移的GDA方法；（4）适用于传播的GDA方法

在索引引用网络数据集上的表现

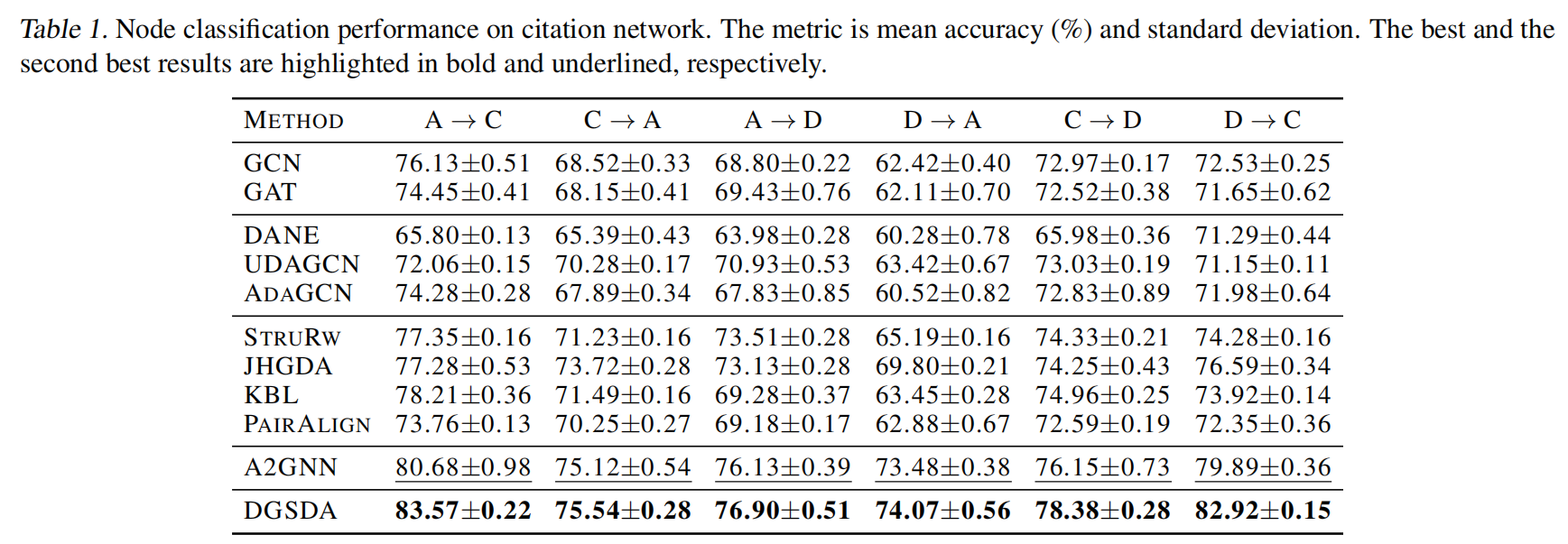
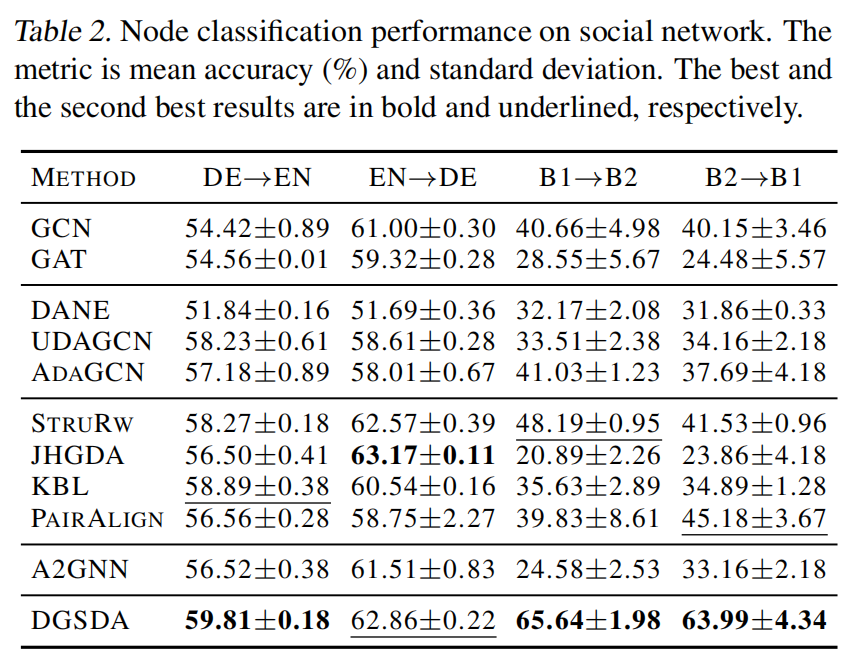
社交网络数据集上的表现

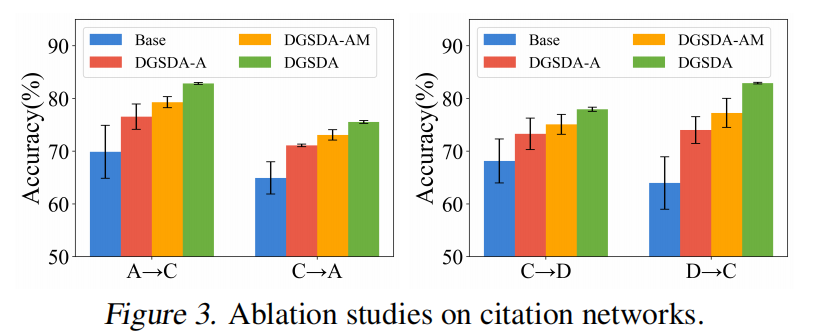
消融实验
针对损失函数中，是否三项都需要考虑的消融实验。

8. 总结

文章结合理论说明，结合实验证明了提出方法的优越之处。
openreview的链接 https://openreview.net/forum?id=846O8wcn8K