论文解读-《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》

1，论文介绍

论文题目：Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
论文范围：图神经网络
论文发表：NIPS，2016

我看网上都把这个叫做ChebyshevNet，那这里就把本文提出的核心算法叫做切比雪夫网络。

本文是基于用在低维度规则化网格数据的CNN，结合谱图理论，提出一个基于图的卷积网络，并给出了数学证明和快速设计基于图的卷积网络的数值方案。
卷积算子是具有平移和旋转不变性的，说明了CNN识别的特征是基于他们的空间位置。
要设计基于图的CNN算法，最大的瓶颈是定义高效学习和丰富表达的本地化图算子。

2. 本文贡献

1，谱图公式，基于图信号的已有的工具，建立了基于图的CNN的谱图理论公式
2，严格本地算子，谱算子应该有着一定的球半径K，K表示到中心点的跳数
3，低计算复杂度
4，有效的池化
5，实验证明，图算法应该和CNN在MNIST上的表现一样优异。

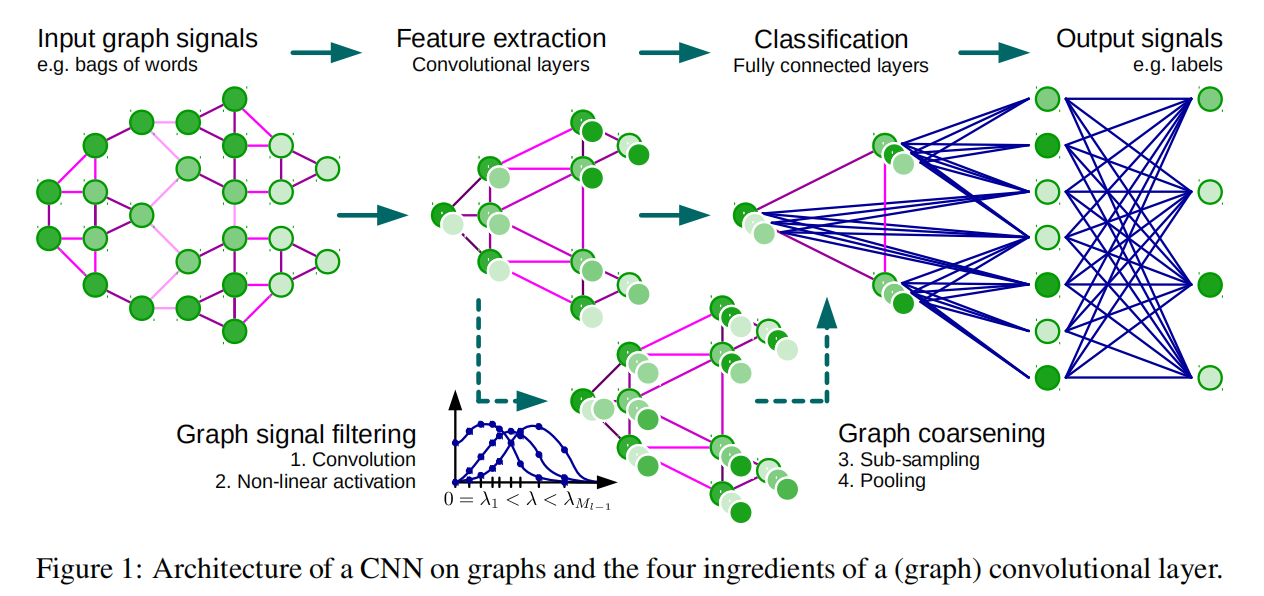
3. 本文算法

设计基于图的CNN模型需要三个基本的步骤：

• 1，设计基于图的本地卷积算子
• 2，将相似顶点同组化的图粗化技术
• 3，将空间分辨率换取更高过滤分辨率的图池化技术

3.1 本地谱域算子

有两种设计卷积算子的策略：空域和谱域。
空域的技术是通过有限尺寸的核操作为局部算子，虽然图卷积在空域上可行，但面临如何选择局部化的邻居
谱域的技术通过卷积在谱域上实现Kronecker delta，为图提供了定位算子。这里的卷积可以定义为在傅里叶基中对角化的线性算子（由拉普拉斯算子的特征向量表示）。谱域中的算子不是自然的局部化的，且转换也是由于图傅里叶基相乘的消耗巨大。这两个限制都可以通过选择特殊的滤波器参数来克服。

图傅里叶变换
对于无向图G=（V，E），其拉普拉斯矩阵是 L = D - A，其中D是节点的度矩阵，A是邻接矩阵。
归一化之后的拉普拉斯矩阵为：

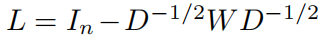
其中I是单位矩阵。
由于拉普拉斯矩阵是对称矩阵，可以进行谱分解，通过变换，可以实现拓扑结构的图到拉普拉斯矩阵，再到谱图；从而实现了空域到谱域的变换。

图信号的谱滤波器
通过g0的滤波信号可以定义为：

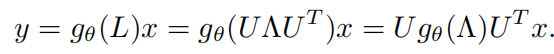
对于该非参数滤波器有着两个较大的缺陷： 在顶点域上的非局域化，学习复杂度o(n)，数据的维度。

局部滤波器的多项式参数化
将滤波器用多项式来进行近似，

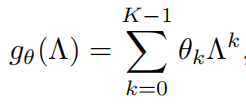
方法的优势：

• 1，拉普拉斯的K阶多项式表示的谱域滤波器正好是K局部化
• 2，学习复杂度为O(K)，为滤波器的大小，和传统的CNN有着相同的复杂度

学习滤波

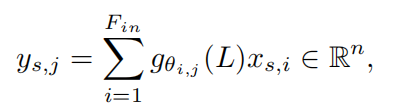
3.2 图粗化技术

该技术是针对图的有意义的邻域，把相似的向量进行聚类组合。多层的池化叠加，类似于图的多尺寸架构，保留局部的几何特征。

图信号的快速池化技术

4. 相关工作

图信号处理这个新兴方向的旨在弥合信号处理与谱图理论之间的鸿沟，是图论和谐波分析的融合。
目标是基础的信号分析算子从规则网格式的数据到图的非规则结构数据转换。

在非欧式空间的CNN

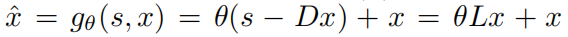
5. 实验设置

简单比较了本文提出的基于图的CNN和经典CNN的效果。效果很接近，但本文算法差了一点。作者猜测是光谱滤波器的各向同性特性导致的。

然后就是跟传统的如线性SVM，多维朴素贝叶斯，softmax 和 FC网络，进行比较。传统的算法都比较简单，本文算法也没有取得绝对性的优势。

6. 结论

本文的理论性比较强，还没有完全理解明白，先记录下目前的理解，后面再回来完善。