专题研究-差分隐私

差分隐私

什么是差分隐私？
差分隐私需要做到的是使得攻击者的知识不会因为新样本的增加而发生变化。针对这个概念最简单直接的定义就如下。

ε 就被称为隐私预算，一般而言， ε 越小，隐私保护越好，但是加入的噪声就越大，数据可用性就下降了

但是在使用过程中，定义的差分隐私太过严格，在实际的应用中需要很多的隐私预算。因此为了算法的实用性，后面引入了松弛版本的差分隐私。本来 ε 是无法bound住，但是我们考虑松弛项 δ ，整体依旧满足差分隐私。一般 δ 都设置的比较小。

差分隐私技术以牺牲一定的数据准确度为代价，能够为用户数据提供严格的隐私保护。
全文分为三个部分：中心化差分隐私，本地化差分隐私，洗牌模型差分隐私。以下逐个进行介绍

中心化差分隐私

函数f表示对数据的统计查询
函数M代表的是差分隐私的随机化机制

对连续型输出结果会用： 加性噪声（Laplace噪声）
对离散型输出结果会用： 指数机制

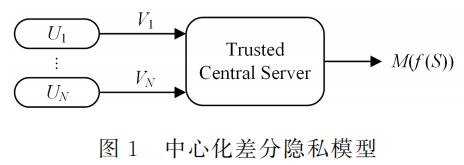
差分隐私能够保护隐私的关键在于为统计信息添加了一定的随机性。适量的随机性可以使得两个相邻数据集发布的统计信息有一定概率相等。

CDP的经典算法

最典型的是适用于数值类型输出的laplace机制，适用于非数值类型输出的指数机制

Laplace机制

著名的加性噪声机制，会向数值型的统计输出结果添加从位置参数为0的Laplace分布中采样得到的噪声。
![[差分隐私007.png]]
敏感度指的是任意两个相邻数据集所得统计输出的最大差值。

Laplace机制的一大好处在于其选择的Laplace概率分布函数。这个概率分布是对称无偏的。

指数机制

对数据集进行的统计查询的输出域一个离散的有限集合。
指数机制定义一个可用性函数映射，为每个数据集和其可能的输出值构成的二元组映射到一个实数值上。

本地化差分隐私

本地化差分隐私模型，和中心化差分隐私的区别：
中心化：噪声添加对象是数据集的统计信息
本地化：噪声添加在原始数据上

噪声扰动机制：基本方法大都是随机响应机制

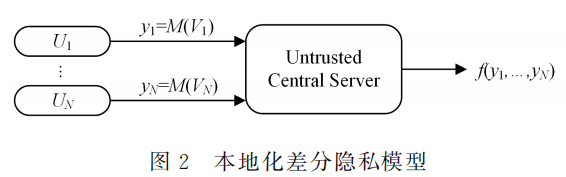
经典算法

一个本地化的随机化算法首先将原始信息进行适当编码，然后在编码的基础上进行随机扰动，掩盖原始信息。

k维随机响应机制

核心思路：来源自回避性回答偏差。
随机响应指的是提交信息的用户以一定的概率提交真实信息，否则随机提交其他信息。

LDP模型中，用户在本地执行随机响应算法后，服务器收集所有扰动值并对各类数据计数，然后使用相应的修正算法计算每类数据的真实频率。

最优一元编码机制（OUE）

一元编码机制，使用了最简单直接的编码方式。每一个原值编码为一个d比特长的特征向量，对向量的每一个比特进行扰动。
效果：每一个仅含一个特征位的特征向量都会被随机化为包含若干个特征位的向量,原始特征位会以较大概率p保留,而非特征位会以较小的概率q反转为特征位。

最优本地哈希机制（OLH）

本地哈希机制，第一部分：通过哈希函数族将原始数据D压缩为更小的数据域G上，第二部分是在压缩后的数据域上部署随机响应。

给定的隐私预算下选择最优的参数g，实现最优的统计精度，即最优本地哈希机制，其估计方差与最优一元编码相同。

k子集选择机制

将一个值映射到值域上的一个大小为k的随机子集。在k-子集选择机制上，每个原始值V以概率p被随机编码为一个包含V在内的k子集，以概率q被随机编码为一个不包含V的k子集。

Hadamard响应机制

一个基于Hadamard矩阵进行编码的LDP机制，利用了Hadamard矩阵的行间距汉明距离大的特点，提高了统计性能，利用快速Walsh-Hadamard变换提高了计算效率。

用于键值数据的LDP机制

对键值类型数据统计的难点在于,键值数据具有两个不同的数据维度,且两个维度之间存在着内在的关联性,因此在对每个维度进行随机化的过程中就必须考虑其中的关联性,若两个维度独立地添加噪声则会对数据效用产生很大影响。

一个名为 PrivKVM 的机制来估计键值数据的频率和均值,考虑到键值相关性,该协议使用了多轮交互的方式迭代地改进对键值的均值估计,当迭代次数足够多时,可证明其均值估计值为原始值的无偏估计量。

针对多维数据的采样方法

一个关键问题是隐私预算的分配，基于组合原理。

差分隐私的后处理优化算法

利用非负性约束和归一性约束对 LDP 的频率查询结果进行后处理的10种机制,并研究分析了不同机制的性能,该工作通过实验证明针对不同的频率查询类型宜使用不同的后处理方法,并给出了详细的后处理方案选择策略,例如针对全数据域的频率估计建议使用 BaseＧCut方法,针对最频繁值的频率估计则应使用Norm 方法。

差分隐私洗牌模型

一种隐私保护的软件监控系统架构，整体架构分为编码器，洗牌器和分析器3个组件，ESA架构
编码器：为用户输入值添加噪声扰动得到随机化输出
洗牌器：将编码器提交的消息进行匿名处理并随机排序，然后转发给分析器
分析器：收集用户的输出并通过修正方法计算得到所需要统计信息的无偏估计量

其中函数Π（x） 表示经过洗牌处理后的顺序

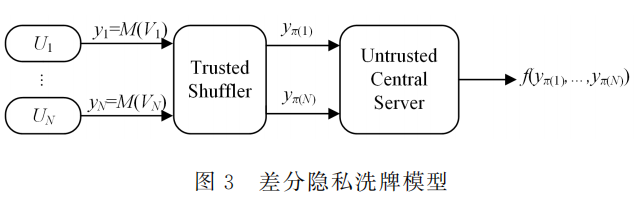
Cheu的工作，单消息洗牌模型 ==> 多消息洗牌协议，分析了差分隐私算法的性能，并证明了洗牌精度的水平严格介于CDP和LDP之间，得出了洗牌模型的可以通过增加消息数来提高精度。

在CDP模式下，随机化机制由受信的服务器执行，主要的考量目标是随机化机制的估计精度。
在LDP和洗牌模型下，用户端需要本地化执行编码和随机化计算，并把结果发给服务器或者洗牌器，需要考虑精度，用户端计算复杂度和通信复杂度，可信洗牌器的高效实现也是一个待优化的问题。

评价指标

误差界：衡量不同差分隐私模型性能的。 分析不同模型在满足 e-差分隐私的条件下解决求和估计问题。

样本复杂度：一个优化问题，e-差分隐私协议对任意数据集S能够以常数概率1-B成功解决该问题至少需要的样本数量N的复杂度。

三种差分隐私的比较

总结

差分隐私感觉目前的使用场景仍然不广泛，多在学术研究领域和一些特殊应用领域。根源在于差分扰动越大带来的不准确度也越高。