cora数据集详解

Cora数据集介绍

该数据集是论文引用图的数据集，数据来自 www.research.whizbang.com/data 。收集了来自机器学习领域内的7个子方向的论文，
一共有2708篇论文，其中相互之间的引用关系5429条关系链。
可用的下载地址： https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz

数据集处理

一般下载的原始数据集是分为三个文件的，如下图所示。

但是在很多仓库里面可以看到作者用的是处理后的数据形式

一般常用的数据是处理之后的数据集合，可以把cora数据集转为了标准的数据形态，把数据转为 ind.cora.x, ind.cora.y, ind.cora.tx, ind.cora.ty, ind.cora.allx, ind.cora.ally, ind.cora.graph;

下面分别介绍各个子集的含义

ind.cora.x 训练集节点特征向量，尺寸为(140, 1433)，保存对象为 scipy.sparse.csr.csr_matrix

ind.cora.tx 测试集节点特征向量，尺寸为(1000, 1433)，保存对象为scipy.sparse.csr.csr_matrix

ind.cora.allx 包含有标签和无标签的训练节点特征向量，可以理解为除测试集以外的其他节点特征集合，训练集是它的子集，保存对象为scipy.sparse.csr.csr_matrix

ind.cora.y one-hot表示的训练节点的标签，保存对象为numpy.ndarray

ind.cora.ty one-hot表示的测试节点的标签，保存对象为numpy.ndarray

ind.cora.ally one-hot表示的ind.cora.allx对应的标签，保存对象为numpy.ndarray

ind.cora.graph 保存节点之间边的信息，保存格式为{index: [index_of_neighbor_nodes]}

ind.cora.test.index 保存测试集节点的索引，保存对象为 list

处理代码注释

# 入口函数，需要加载cora数据调用这个即可
def load_ind_cora_data(cora_path):
	x, y, tx, ty, allx, ally, graph, test_index = load_ind_cora_pkl(cora_path)
	train_index = np.arange(y.shape[0])					# 训练集的范围 [0, ysize)
	val_index = np.arange(y.shape[0], y.shape[0] + 500)	# 验证集的范围 [ysize, ysize+500)
	sorted_test_index = sorted(test_index)				# 测试集的范围 

	x = np.concatenate((allx, tx), axis=0)		# 全体的X数据
	y = np.concatenate((ally, ty), axis=0).argmax(axis=1)	# 全体的Y数据

	x[test_index] = x[sorted_test_index]
	y[test_index] = y[sorted_test_index]
	num_nodes = x.shape[0]

	train_mask = np.zeros(num_nodes, dtype='bool')
	val_mask = np.zeros(num_nodes, dtype='bool')
	test_mask = np.zeros(num_nodes, dtype='bool')

	train_mask[train_index] = True
	val_mask[val_index] = True
	test_mask[test_index] = True

	adj_matrix = build_adjacency(graph)		# 构建邻接矩阵
	return x, y, adj_matrix, train_mask, val_mask, test_mask

根据上面的入口函数来看加载函数

# 从磁盘中加载文件
def load_ind_cora_pkl(cora_path):
	dataset_str = 'cora'
	names = ['x', 'y', 'tx', 'ty', 'allx', 'ally', 'graph', 'test.index']
	objects = []
	for i in range(len(names)):
		file_path = os.path.join(cora_path, 'ind.{}.{}'.format(dataset_str, names[i]))
		if names[i] == 'test.index':
			out = np.genfromtxt(file_path, dtype='int64')   # test.index是一个文本类型，直接从文本里获取数组
		else:
			out = pkl.load(open(file_path, 'rb'), encoding="latin1") # 从二进制加载原数据类型
			out = out.toarray() if hasattr(out, 'toarray') else out
		objects.append(out)

	x, y, tx, ty, allx, ally, graph, test_index = tuple(objects)
	# x, tx, allx 类型是 scipy.sparse._csr.csr_matrix 存储的是样本
	# y, ty, ally 类型是 numpy.ndarray, [3, 4, 3...] 存储的是标签
	# graph 类型是 collections.defaultdict  {node: [adjnode1, adjnode2,...]}
	return x, y, tx, ty, allx, ally, graph, test_index

邻接矩阵的处理过程

# 传入的是一个以节点为key以邻接节点数组为value的dict，返回一个稀疏矩阵
def build_adjacency(adj_dict):
	edge_index = []
	num_nodes = len(adj_dict)   # 2708,点的总数
	for src, dst in adj_dict.items():
		edge_index.extend([src, v] for v in dst)
		edge_index.extend([v, src] for v in dst)
		# 这里用的是无向图 （那么引用-被引用 ，和 被引用 - 引用，两条边都需要加入）
	edge_index = list(k for k, _ in itertools.groupby(sorted(edge_index)))
	edge_index = np.asarray(edge_index)
	# 把所有的邻接边都收入到一个list里面 ，格式为 [[node1, node2], [node1, node3], ...]
	adj_matrix = sp.coo_matrix((np.ones(len(edge_index)), 
								(edge_index[:, 0], edge_index[:, 1])),
								shape=(num_nodes, num_nodes), 
								dtype='float32')
	# 将edge_index类型，转为adj_matrix，转为稀疏矩阵
	return adj_matrix

针对上面得到的邻接矩阵，需要进行归一化处理，代码如下

# 传入的是一个稀疏矩阵，返回一个稀疏矩阵
def normalization(adj_matrix):
	adj_matrix += sp.eye(adj_matrix.shape[0])   # 邻接矩阵需要把对角线置为1
	degree = np.asarray(adj_matrix.sum(1))		# 对邻接矩阵的行求和得到每一个节点的度向量
	d_hat = sp.diags(np.power(degree, -0.5).flatten()) # 根据度向量 求得 每一行的归一化分母
	return d_hat.dot(adj_matrix).dot(d_hat).tocoo()   # 归一化处理，并转为稀疏矩阵存储

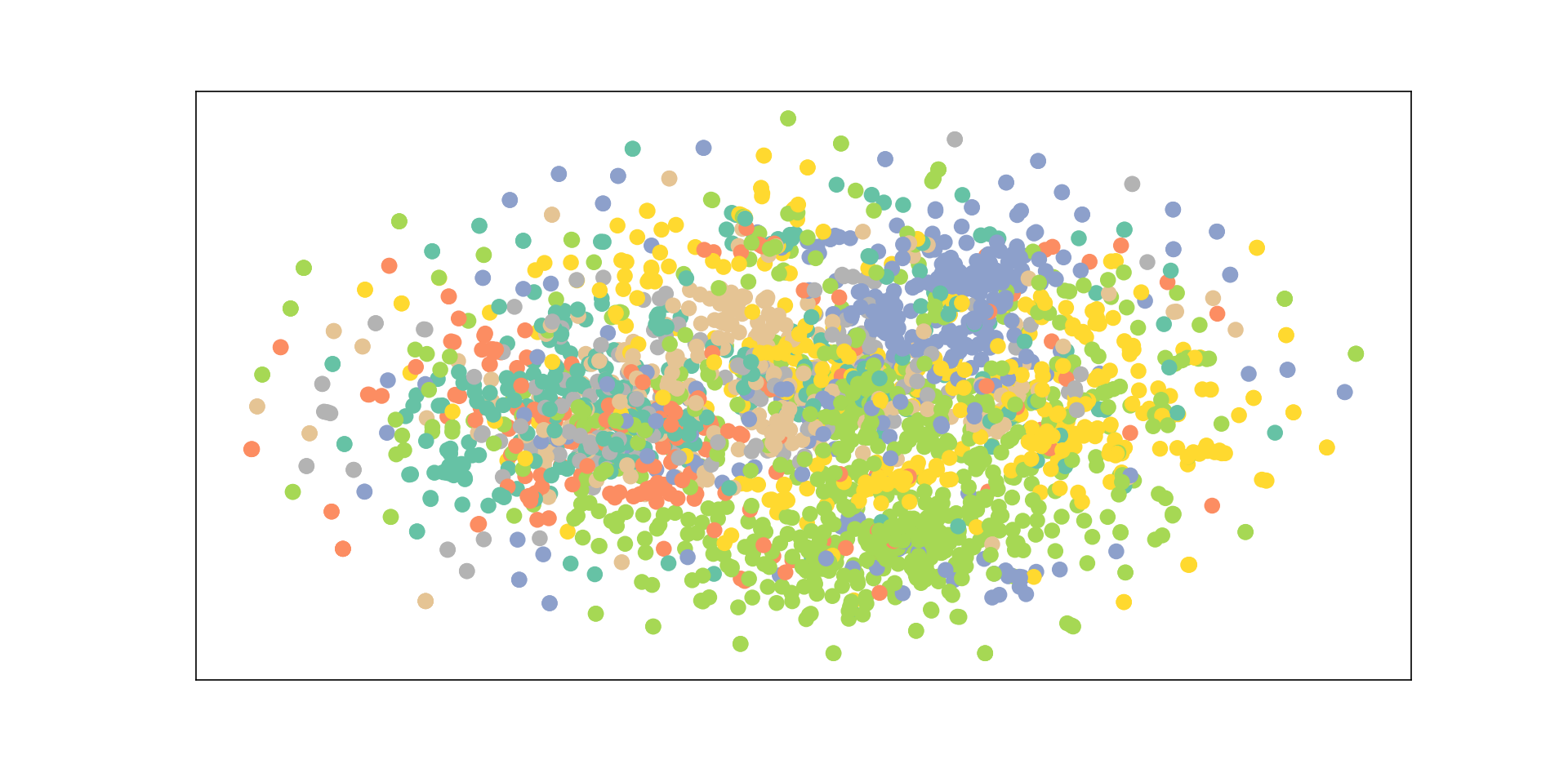
进一步分析x的分布结构，使用代码进行分析

# 使用TSNE进行x和y的可视化
def visualize(x, y):
    z = TSNE(n_components=2).fit_transform(x) 
    plt.figure(figsize=(10,10))
    plt.xticks([])
    plt.yticks([])

    plt.scatter(z[:, 0], z[:, 1], s=70, c=y, cmap="Set2")
    plt.show()

visualize(x, y)

得到如下的分析图

总结

数据简单，数据量小，应用范围广，经典数据集