Spearman相关系数

Spearman相关系数

斯皮尔曼相关系数，其对数据的分布要求较低，而且衡量的是两个变量之间的单调关系（即一个变量增加时，另一个变量也增加或减少，但不一定是线性关系）。因此，即使变量之间的关系是非线性的，只要关系是单调的，斯皮尔曼相关系数仍然可以有效地衡量它们之间的相关性。

计算方式

首先我们要计算排名，所谓排名就是将数据由大到小排列，然后给每个数据一个等级。最大是数等级就为1。但是，如果有相同的排名，我们就得给它们合理的排名，一般是取平均值。比如一组数1，2，2，4，5，那么它们的排名分别是1，2.5，2.5，4，5。基于这个排名我们再开始如下计算。

---

① 无结（无相同名次）时的公式

\[r_s = 1 - \frac{6 \sum_1^n d_i^{2}}{n(n^{2}-1)} \]

• \(r_s\)：斯皮尔曼相关系数
• \(d_i\)：第 \(i\) 对数据的等级差（两个变量对应观测值的等级之差）
• \(n\)：样本数量
• \(\sum_1^n d_i^{2}\)：所有等级差的平方和

---

② 存在“结”（相同名次）时的修正公式

\[r_s = \frac{\sum_1^n (R_i - \bar{R})(S_i - \bar{S})}{\sqrt{\sum_1^n (R_i - \bar{R})^{2} \sum_1^n (S_i - \bar{S})^{2}}} \]

• \(R_i\)：第一个变量的等级
• \(S_i\)：第二个变量的等级
• \(\bar{R},\; \bar{S}\)：两个变量等级的平均值

---

取值含义

取值范围： [-1, 1]

\(r_s\) 值	解释
+1	完全正单调相关（一个变量递增，另一个也严格递增）
−1	完全负单调相关（一个变量递增，另一个严格递减）
0	无单调相关关系

计算p值

我们还将计算P值来进一步反映相关性，在统计语言表达上，如果P值小于0.01，则称作0.01水平显著，则说明X对Y存在影响关系这件事至少有99％的把握，统计语言描述为X在0.01水平上呈现显著性。如果P值小于0.05(且大于或等于0.01)，则称作在0.05水平上显著。反之，如果P值较大则说明显著性比较小。

Python代码

其中的计算数据来源某道数学建模题目。

import numpy as np
from scipy.stats import rankdata, t as tdist
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import zhplot

def spearman_manual(x, y, method='average'):
    """
    手动实现 Spearman 相关系数及其 p 值（双侧）
    参数
    ----
    x, y : 一维数组，长度相同
    method : rankdata 的并列值处理方式，默认 'average'

    返回
    ----
    rs : Spearman 相关系数
    p  : 双侧检验 p 值
    """
    x, y = np.asarray(x), np.asarray(y)
    if x.size != y.size:
        raise ValueError("x 与 y 长度必须相同")
    n = x.size
    if n < 3:                      # 自由度 n-2 >=1 才有意义
        return np.nan, np.nan

    # 1. 计算等级
    Rx = rankdata(x, method=method)
    Ry = rankdata(y, method=method)

    # 2. 检测是否有结
    ties = (len(np.unique(Rx)) != n) or (len(np.unique(Ry)) != n)

    # 3. 计算 rs
    if not ties:
        # 无结：经典公式
        d = Rx - Ry
        d2_sum = np.dot(d, d)
        rs = 1.0 - 6.0 * d2_sum / (n * (n**2 - 1))
    else:
        # 有结：等级后的 Pearson
        R_bar, S_bar = Rx.mean(), Ry.mean()
        numerator = np.sum((Rx - R_bar) * (Ry - S_bar))
        denominator = np.sqrt(np.sum((Rx - R_bar)**2) * np.sum((Ry - S_bar)**2))
        rs = numerator / denominator

    # 4. 计算双侧 p 值（t 检验，df = n-2）
    if abs(rs) >= 1.0:            # 防止除 0
        p = 0.0 if rs != 0 else 1.0
    else:
        t_stat = rs * np.sqrt((n - 2) / (1 - rs**2))
        p = 2 * tdist.sf(abs(t_stat), df=n - 2)

    return rs, p

# 输出结果
# 1. 读数据 -------------------------------------------------------------
data = np.loadtxt('B-附件1.csv', delimiter=',', dtype=float,
                  skiprows=2, encoding='utf-8', usecols=[1, 2, 3, 13, 14, 15, 16])

# 2. 变量名 -------------------------------------------------------------
x_names = ['X1', 'X2', 'X3']
y_names = ['Y1', 'Y2', 'Y3', 'Y4']

# 3. 计算并汇总 ---------------------------------------------------------
records = []
for i, xn in enumerate(x_names):
    for j, yn in enumerate(y_names):
        rs, p = spearman_manual(data[:, i], data[:, 3 + j])
        records.append({'X变量': xn, 'Y变量': yn,
                        '相关系数': rs, 'p值': p})

# 4. 输出表格 -----------------------------------------------------------
df = pd.DataFrame(records)
print(df)


# 绘制热力图
# 1. 把结果表 pivot 成 3×4 矩阵 -------------------------------
corr_mat = df.pivot(index='X变量', columns='Y变量', values='相关系数')

# 2. 画图 ------------------------------------------------------
plt.figure(figsize=(4, 3))                       
sns.heatmap(corr_mat,
            annot=True,
            fmt='.3f',
            cmap='coolwarm',
            annot_kws={'size': 20}) 
plt.title('Spearman 相关系数热力图',fontsize=25)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.tight_layout()
plt.xlabel('')                               
plt.ylabel('')
plt.show()

输出结果

  X变量 Y变量      相关系数            p值
0   X1  Y1 -0.191580  1.611606e-01
1   X1  Y2  0.459110  4.224245e-04
2   X1  Y3 -0.530383  3.113766e-05
3   X1  Y4 -0.013273  9.233794e-01
4   X2  Y1  0.130301  3.430326e-01
5   X2  Y2  0.614357  6.067929e-07
6   X2  Y3  0.039024  7.772779e-01
7   X2  Y4 -0.572480  4.953330e-06
8   X3  Y1 -0.181354  1.851435e-01
9   X3  Y2  0.422558  1.310038e-03
10  X3  Y3 -0.241051  7.625124e-02
11  X3  Y4 -0.038841  7.782967e-01

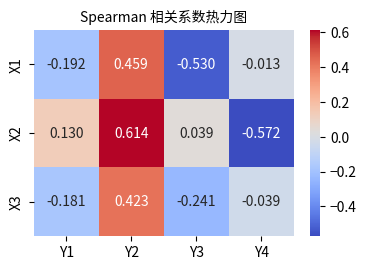
绘制热力图