《白话机器学习的数学》-感知机Perceptron

《白话机器学习的数学》-感知机Perceptron

感知机（Perceptron）是机器学习领域中一种经典的线性分类模型，它以简单的数学原理为基础，为后续复杂的人工神经网络和机器学习算法奠定了坚实的理论基础。

我在近期阅读《白话机器学习中的数学》这本书时学习到了这个代码。作者只是介绍了这个模型的一个很简单的作用——分类。这也是机器学习的一个很重要的功能。

本文基于这本书，先介绍感知机的数学原理，再介绍感知机的简单运用：分类横向和纵向图片。

一、感知机的数学模型

感知机的结构非常简洁，主要由输入层和输出层组成。假设我们有一个数据集 \(\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\)，其中 \(x_i \in \mathbb{R}^d\) 是输入特征向量，在我们后续的应用中\(x_i\)就是二维向量，分别表示照片的宽和高，\(y_i \in \{-1, +1\}\) 是对应的类别标签。感知机的目标是找到一个线性决策边界，将不同类别的数据分开。

首先我们需要随机预设一个参数向量 \(\boldsymbol{w}\)。

根据参数向量 \(\boldsymbol{x}\) 来判断图像是横向还是纵向的函数，即返回 1 或者 -1 的函数 \(f_{\boldsymbol{w}}(\boldsymbol{x})\)的定义如下。这个函数被称为判别函数。

\[f_{\boldsymbol{w}}(\boldsymbol{x}) = \begin{cases} 1 & (\boldsymbol{w} \cdot \boldsymbol{x} \geqslant 0) \\ -1 & (\boldsymbol{w} \cdot \boldsymbol{x} < 0) \end{cases} \]

在这个基础上，我们可以这样定义权重向量的更新表达式。

\[\boldsymbol{w} := \begin{cases} \boldsymbol{w} + y^{(i)} \boldsymbol{x}^{(i)} & (f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) \neq y^{(i)}) \\ \boldsymbol{w} & (f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) = y^{(i)}) \end{cases} \]

这个更新表达式的含义是：如果当前的输入向量 \(\boldsymbol{x}^{(i)}\) 被错误分类，则更新权重向量 \(\boldsymbol{w}\)，更新的方向是往\(w\)和\(y^{(i)} \boldsymbol{x}^{(i)}\)做矢量合成的方向，遵循平行四边形法则,这样的好处是下次正确分类的可能性很更高（我这里举的例子是线性可分的，要是线性不可分，就没法保证更新的方向是正确的）；如果当前的输入向量 \(\boldsymbol{x}^{(i)}\) 被正确分类，则不更新权重向量 \(\boldsymbol{w}\)。

二、感知机的简单运用代码

在写代码前我们得准备好数据。

x1,x2,y
153,432,-1
220,262,-1
118,214,-1
474,384,1
485,411,1
233,430,-1
396,361,1
484,349,1
429,259,1
286,220,1
399,433,-1
403,340,1
252,34,1
497,472,1
379,416,-1
76,163,-1
263,112,1
26,193,-1
61,473,-1
420,253,1

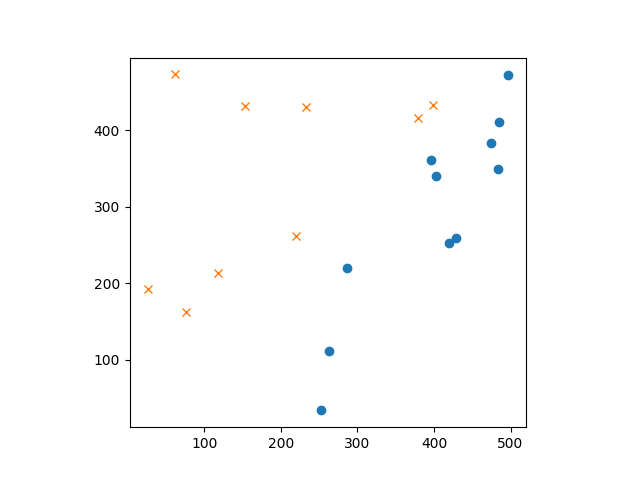
先绘制图像了解下数据分布。

import numpy as np
import matplotlib.pyplot as plt

train = np.loadtxt('date_2.csv', delimiter=',', skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]

# 绘图
# 绘制训练数据中标签为1的样本的第一和第二特征，使用圆圈标记
plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1], 'o')
# 绘制训练数据中标签为-1的样本的第一和第二特征，使用叉号标记
plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1], 'x')
# 设置坐标轴为等比例缩放
plt.axis('scaled')
plt.show()

绘图结果：

训练模型：

# 权重的初始化
w = np.random.rand(2)

# 判别函数
def f(x):
    if np.dot(w, x) >= 0:
        return 1
    else:
        return -1
    
# 重复次数
epoch = 10

# 更新次数
count = 0

# 学习权重
for _ in range(epoch):
    for x, y in zip(train_x, train_y):
        if f(x) != y:
            w = w + y * x
            # 输出日志
            count += 1
            #print(' 第{} 次: w = {}'.format(count, w))
            print(f'这是第{count}次更新,w={w}')

x1 = np.arange(0, 500)

plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1],
'o')
plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1],
'x')
plt.plot(x1, -w[0] / w[1] * x1, linestyle='dashed')
plt.show()

绘图展示：

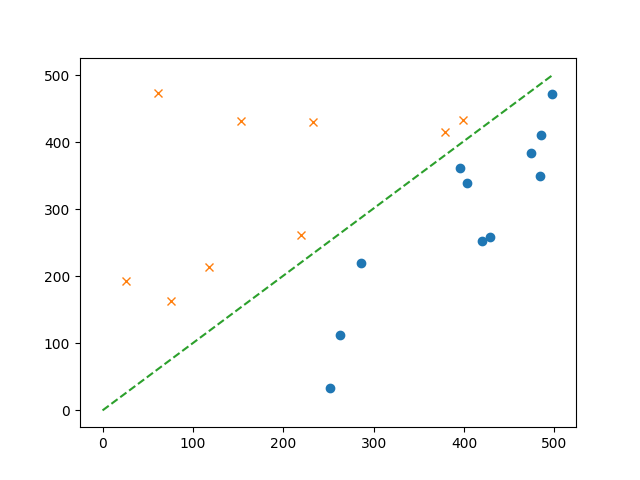
事实上，预设的epoch=10偏大，在实际测试中epoch=4就已经有很理想的结果了。

epoches=4的日志结果：

这是第1次更新,w=[-152.15910092 -431.26278945]
这是第2次更新,w=[321.84089908 -47.26278945]
这是第3次更新,w=[  88.84089908 -477.26278945]
这是第4次更新,w=[ 484.84089908 -116.26278945]
这是第5次更新,w=[  85.84089908 -549.26278945]
这是第6次更新,w=[ 488.84089908 -209.26278945]
这是第7次更新,w=[ 109.84089908 -625.26278945]
这是第8次更新,w=[ 372.84089908 -513.26278945]
这是第9次更新,w=[ 846.84089908 -129.26278945]
这是第10次更新,w=[ 613.84089908 -559.26278945]
这是第11次更新,w=[ 214.84089908 -992.26278945]
这是第12次更新,w=[ 617.84089908 -652.26278945]
这是第13次更新,w=[1114.84089908 -180.26278945]
这是第14次更新,w=[ 735.84089908 -596.26278945]
这是第15次更新,w=[ 515.84089908 -858.26278945]
这是第16次更新,w=[ 989.84089908 -474.26278945]
这是第17次更新,w=[ 756.84089908 -904.26278945]
这是第18次更新,w=[1152.84089908 -543.26278945]
这是第19次更新,w=[ 753.84089908 -976.26278945]
这是第20次更新,w=[1156.84089908 -636.26278945]
这是第21次更新,w=[  777.84089908 -1052.26278945]
这是第22次更新,w=[1251.84089908 -668.26278945]
这是第23次更新,w=[ 1018.84089908 -1098.26278945]
这是第24次更新,w=[1515.84089908 -626.26278945]
这是第25次更新,w=[ 1136.84089908 -1042.26278945]

完整代码：

#感知机
import numpy as np
import matplotlib.pyplot as plt

train = np.loadtxt('date_2.csv', delimiter=',', skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]

# 绘图
# 绘制训练数据中标签为1的样本的第一和第二特征，使用圆圈标记
plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1], 'o')
# 绘制训练数据中标签为-1的样本的第一和第二特征，使用叉号标记
plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1], 'x')
# 设置坐标轴为等比例缩放
plt.axis('scaled')
plt.show()

# 权重的初始化
w = np.random.rand(2)

# 判别函数
def f(x):
    if np.dot(w, x) >= 0:
        return 1
    else:
        return -1
    
# 重复次数
epoch = 4

# 更新次数
count = 0

# 学习权重
for _ in range(epoch):
    for x, y in zip(train_x, train_y):
        if f(x) != y:
            w = w + y * x
            # 输出日志
            count += 1
            #print(' 第{} 次: w = {}'.format(count, w))
            print(f'这是第{count}次更新,w={w}')

x1 = np.arange(0, 500)

plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1],
'o')
plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1],
'x')
plt.plot(x1, -w[0] / w[1] * x1, linestyle='dashed')
plt.show()

三、总结

其实我们可以看到感知机还是比较简单的，但书中提到感知机虽然简单，但它是神经网络和深度学习的基础模型，所以记住它没坏处。