2025年城阳一中第一届ACM 校赛 (CYCPC) 题解
2025年城阳一中第一届ACM 校赛 (CYCPC) 题解
本场比赛的大概难度排序为:
Easy:A,L,H,D
Medium:F,E
Medium Hard:I,C,K,J
Hard:B,G,M
A
由于题目中字符串长度 n 较小,直接通过三重循环枚举所有可能的 (i,j,k) 组合(满足 i<j<k),判断是否构成 “QAQ” 即可。
使用线性的 dp 做法,亦或是枚举 A 算贡献的做法,都可以通过此题。
你还会发现这是一个子序列自动机的板子,总之什么做法好像都能过。
void solve() {
string s;
int cnt = 0;
cin >> s;
for (int i = 0;i < s.size();i++) {
for (int j = i + 1;j < s.size();j++) {
for (int k = j + 1;k < s.size();k++) {
if (s[i] == 'Q' && s[j] == 'A' && s[k] == 'Q')cnt++;
}
}
}
if(cnt) cout << "YES";
else cout << "NO";
}
L
原式等于
使用前缀和计算即可。
void solve() {
int n;
cin >> n;
vector<ll>a(n), pre(n + 1, 0);
for (int i = 0;i < n;i++)cin >> a[i];
for (int i = n - 1;i >= 0;i--) {
pre[i] = a[i] + pre[i + 1];
}
ll sum = 0;
for (int i = 0;i < n - 1;i++) {
sum += a[i] * pre[i + 1];
}
cout << sum << endl;
}
H
简单 DP ,设 \(f_{i,j}\) 表示前 \(i\) 个数,将最后一位变为 \(j\) 且前 \(i\) 个数单调不减的最小代价,得到转移方程 \(f_{i,j} = min_{0 \le k \le j} + dis(a_i,j)\),反方向设计类似的状态 \(g_{i,j}\) ,答案即为:
const int N = 1e6+10;
int pre[N][10],suf[N][10];
inline int f(int x,int y){return std::min(abs((x-y+10)%10),abs((y-x+10)%10));}
inline void solve()
{
int n; fin >> n;int ans = inf;
std::vector<int> a(n+1);
for(int i = 1;i <= n;i++)
for(int j = 0;j <= 9;j++)
pre[i][j] = suf[i][j] = inf;
for(int i = 1;i <= n;i++) fin >> a[i];
for(int i = 1;i <= n;i++)
for(int j = 0;j <= 9;j++)
for(int k = 0;k <= j;k++)
pre[i][j] = std::min(pre[i][j],pre[i-1][k]+f(a[i],j));
for(int i = n;i >= 0;i--)
for(int j = 0;j <= 9;j++)
for(int k = 0;k <= j;k++)
suf[i][j] = std::min(suf[i][j],suf[i+1][k]+f(a[i],j));
for(int i = 1;i <= n;i++)
for(int j = 0;j <= 9;j++)
ans = std::min(ans,pre[i][j]+suf[i][j]-f(a[i],j));
fout << ans << '\n';
}
D
https://codeforces.com/problemset/problem/1365/E
发现取三个数时,能得到的答案最大(这里读者可以自行证明),而此时你会发现价值即为选出的三个数的位或值,\(O(n^3)\) 枚举一下选哪些数就可以了。
void solve()
{
int n; cin>>n;
vector<int>a(n+1);
for(int i=1;i<=n;i++)cin>>a[i];
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
ans=max(ans,a[i]|a[j]|a[k]);
cout<<ans<<'\n';
}
F
https://codeforces.com/problemset/problem/466/D
设 \(c_i = m - a_i\) ,表示每个点 \(i\) 需要加法的次数,若某个 \(c_i < 0\)
时则无解。
然后设计状态 \(f_{i,j,0/1}\) 表示处理了前 \(i\) 个位置,还有 \(j\) 个 \(l\) 端点未匹配,点 \(i\) 是否同时放置了一个 \(l\) 和一个 \(r\) 。
得出转移方程:
\(f_{i+1,j,0} = f_{i,j,0} + f_{i,j,1}\)
\(f_{i+1,j+1,0} = f_{i,j,0} + f_{i,j,1}\)
\(f_{i+1,j-1,0} = (f_{i,j,0} + f_{i,j,1}) \times j\)
\(f_{i+1,j,1} = (f_{i,j,0} + f_{i,j,1}) \times (j+1)\)
答案即为 \(f_{n,0,0} + f_{n,0,1}\)。
void solve()
{
cin >> n >> m;
int ok = 1;
for(int i = 1;i <= n;i++) {cin >> a[i]; ok &= (a[i]>=0);}
for(int i = 1;i <= n;i++) a[i] = m - a[i];
if(!ok) return void(cout << "0\n");
f[0][0][0] = 1;
for(int i = 0;i <= n-1;i++)
for(int j = 0;j <= i;j++)
{
if(j==a[i+1])
(f[i+1][j][0]+=f[i][j][0]+f[i][j][1])%=mod;
if(j+1==a[i+1])
(f[i+1][j+1][0]+=f[i][j][0]+f[i][j][1])%=mod;
if(j==a[i+1])
(f[i+1][j-1][0]+=(f[i][j][0]+f[i][j][1])*j%mod)%=mod;
if(j==a[i+1]-1)
(f[i+1][j][1]+=(f[i][j][0]+f[i][j][1])*(j+1))%=mod;
}
cout << (f[n][0][0]+f[n][0][1]) % mod;
}
E
https://codeforces.com/problemset/problem/1152/D
这里有一个有趣的贪心,我们只需要选定所有深度为偶数的点和其父节点匹配即可做到最大匹配,此时我们可以发现我们覆盖了全部深度为奇数的点,而所有边都连接两个深度奇偶不同的点,所以这道题的答案即为 trie 树上深度为奇数的点的个数。
设计状态 \(f_{i,j}\) 表示有 \(i\) 个左括号 \(j\) 个右括号,且是合法的括号序列前缀的括号序列的个数。
得到转移方程:
答案即为:
void solve()
{
cin>>n; f[1][1]=1;
for(i=2;i<=n+1;i++)
for(j=1;j<=i;j++)
f[i][j]=(f[i-1][j]+f[i][j-1])%mod;
for(int i = 2;i <= n+1;i++)
for(int j = 1;j <= i;j++)
if((i+j)&1)
(ans+=f[i][j]) % mod;
cout<<ans%mod;
}
I
https://www.luogu.com.cn/problem/P7386
两个方法,一个容斥方向的做法,一个考虑组合意义的做法。
这里讲述第二个方法,首先将题目含义转换到字典树,即为统计字典树节点的数量。
我们将一个 \(A\) 与一个 \(B\) 捆绑到一起,设状态 \(f_{i,j}\) 表示含有 \(i\) 个的 \(BA\) ,\(j\) 个 \(B\) 的情况下的字典树节点数量,画一下图,可以发现:
边界条件为 \(f_{1,j} = j + 2 , f_{i,0} = 2i\) 。
考虑组合意义,我们可以计算出每个 \(f_{1,j}\) 对答案产生的贡献,以及每个常数 \(2\) 产生的贡献,本质就是从某个位置走到终点的路径数量,插板法计算即可,然后使用平行求和法 / 上指标求和进行化简,最后可得答案即为:
const int N = 19000005;
// 组合数预处理
int fac[N],inv[N];
inline void init()
{
fac[0] = 1;
for (int i = 1; i <= N-5; ++i)
fac[i] = fac[i - 1] * i % mod;
inv[1] = 1;
for (int i = 2; i <= N-5; ++i)
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
inv[0] = 1;
for (int i = 1; i <= N-5; ++i)
inv[i] = inv[i - 1] * inv[i] % mod;
}
int C(int n,int m)
{
if(n < m) return 0;
else return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int lucas(int n,int m)
{
if(!m) return 1;
return lucas(n/mod,m/mod) * C(n%mod,m%mod)%mod;
}
int ans = 0;
void solve()
{
int n,m; fin >> n >> m;
if(n > m) return ;
ans ^= (2 * lucas(m+1,n) % mod - lucas(m-1,n) + mod - 2 + mod) % mod;
}
C
https://codeforces.com/problemset/problem/1346/H
考虑线段中心是 \((l + r) / 2\),我们发现 Cirno(琪露诺) 和 Daiyousei(大妖精) 可以选择对称策略,使得线段不会偏离中心。
设起始段 \([l, r]\),那么考虑能到达的最近的中心相同的 \([l', r']\),那么需要 \(l' - l\) 步。考虑偏移一格,要到达中心偏左一个单位的线段 \([l', r']\) 需要 \(l - l' - 1\) 步,要到达中心偏右一个单位的线段 \([l', r']\) 需要 \(l - l' + 1\) 步。
分别设为 \(step_{center}, step_l, step_r\),
特别地,若没有符合的线段,设为 inf。
那么答案就是 \(\max(\min(step_{center}, step_l), \min((step_{center}, step_r)))\);
这是因为,假设 Cirno 已经选了,如果是 \([l + 1, r]\),那么 Daiyousei 可以到达 \([l + 2, r]\),那么可以到达 \(step_r\),因为之后可以做对称操作,使得中心不变;Daiyousei 也可以到达 \([l + 1, r - 1]\),到达 \(step_{center}\);Dayyousei 不能到达更优的点,因为 Cirno 可以进行对称操作,使得中心偏移不会超过 1。
\([l, r - 1]\) 也是同理的。
所以第一步 Cirno 会取 max。
找到 step 是简单的,对每个 center 开一个桶,直接 lower_bound 查询即可。
#include<bits/stdc++.h>
using i64 = long long;
using u32 = unsigned int;
using u64 = unsigned long long;
using pii = std::pair<int, int>;
template<typename T> int sz(const T& x) { return int(x.size()); }
template<typename T> void chmin(T& lhs, T rhs){ if((rhs) < lhs){ lhs = (rhs);}}
template<typename T> void chmax(T& lhs, T rhs){ if((rhs) > lhs){ lhs = (rhs);}}
const int V = 2e6;
int N, Q;
std::vector<std::vector<int> > ranges(2 * V);
struct Range{
int l, r;
};
std::set<int> key;
std::vector<Range> query;
void input(){
std::cin >> Q >> N;
query.resize(Q);
for(int i = 0; i < Q; i++){
std::cin >> query[i].l >> query[i].r;
}
for(int i = 0; i < N; i++){
int l, r;
std::cin >> l >> r;
--l;
ranges[l + r].push_back(l);
key.insert(l + r);
}
}
void interact(){
for(int k : key){
std::sort(ranges[k].begin(), ranges[k].end());
}
auto get = [&](int l, int r) -> int{
int sum = l + r;
if(not ranges[sum].empty() and ranges[sum].back() >= l){
auto it = std::lower_bound(ranges[sum].begin(), ranges[sum].end(), l);
return *it - l;
} else {
return INT_MAX;
}
};
for(int t = 0; t < Q; t++){
int l = query[t].l, r = query[t].r;
--l;
int L = get(l, r - 2);
int keep = get(l, r);
int R = get(l + 2, r);
int ans = std::max(std::min(keep, L == INT_MAX ? INT_MAX : L + 1), std::min(keep, R == INT_MAX ? INT_MAX : R + 1));
if(ans == INT_MAX){
std::cout << -1 << " \n"[t == Q - 1];
} else {
std::cout << ans << " \n"[t == Q - 1];
}
}
}
signed main(){
std::cin.tie(0);
std::ios::sync_with_stdio(0);
input();
interact();
return 0;
}
K
https://codeforces.com/problemset/problem/935/F
设 \(delta_i = a_{i + 1} - a_i\)。当前波动强度,设为 \(sum\),即为 \(\sum_{i=1}^{n-1} |delta_i|\) 。
修改 \([l, r]\) 只会修改 \(delta_{l - 1}, delta_l, delta_r, delta_{r+1}\) 直接更新 \(delta\) 即可。
查询操作是,\(a_i\) \(\leftarrow a_i + x\),最大化 \(sum\)。
那么
\(delta_{i-1} \leftarrow (a_i + x) - a_{i-1} = delta_{i-1} + x\)
\(delta_i \leftarrow a_{i+1} - (a_i + x) = delta_i - x\)
增加
\((|delta_{i-1} + x| - |delta_{i-1}|) + (|delta_i - x| - |delta_i|)\)
我们希望最大化这个东西。
-
边界 \(i = 1\) 或 \(i = N\)
特判,尝试更新答案
否则:
-
峰 : \(delta_{i-1} \ge 0 \land delta_i \le 0\)
增加 \(x + x = 2x\)
-
降 :\(delta_{i-1} \lt 0 \land delta_i \le 0\)
\(delta_{i-1} + x \ge 0\) 时,增加 \(((delta_{i-1} + x) - (-delta_{i-1})) + x = 2 * x + 2 * delta_i\)
\(delta_{i-1} + x \lt 0\) 时,增加 \((-delta_{i-1} - x - (-delta_{i-1}|) + x = 0\)
绝对值更小的 \(delta_{i-1}\) 是更优的。
-
增 : \(delta_{i-1} \ge 0 \land delta_i \gt 0\)
和 降 对称,绝对值更小的 \(delta_i\) 是更优的。
-
谷 \(delta_{i-1} \lt 0 \land delta_i \gt 0\)
这个太困难了。CatNyan 不会做。但是我们发现,只要有两个谷,就有一个峰,我们肯定选峰。所以暴力找第一个谷尝试更新答案即可。
用两个 set 维护峰和谷,用线段树维护区间绝对值最小的 降的 \(delta_i\) 和升的 \(delta_{i-1}\) 即可。
与题解不同,代码由 0 作为下标开头。
#include<bits/stdc++.h>
using i64 = long long;
template<typename T> int sz(const T& x) { return int(x.size()); }
template<typename T> void chmax(T& lhs, T rhs){ if((rhs) > lhs){ lhs = (rhs);}}
template<typename Info>
struct SegmentTree{
int X;
std::vector<Info> info;
#define lc (i * 2)
#define rc (i * 2 + 1)
#define mid ((l + r) / 2)
inline void pull(int i){
info[i] = info[lc] + info[rc];
}
void build(int i, int l, int r, std::vector<Info>& a){
if(l + 1 == r){
info[i] = a[l];
return;
}
build(lc, l, mid, a), build(rc, mid, r, a);
pull(i);
}
void init(std::vector<Info> a){
info.assign(4 * X, Info());
build(1, 0, X, a);
}
SegmentTree(int X_){
X = X_;
init(std::vector<Info>(X, Info()));
}
void modify(int i, int l, int r, int p, Info v){
if(l + 1 == r){
info[i] = v;
return;
}
if(p < mid) modify(lc, l, mid, p, v);
else modify(rc, mid, r, p, v);
pull(i);
}
void modify(int p, Info v){
modify(1, 0, X, p, v);
}
Info rangeQuery(int i, int l, int r, int b, int e){
if(b <= l and r <= e){
return info[i];
}
if(r <= b or e <= l){
return Info();
}
return rangeQuery(lc, l, mid, b, e) + rangeQuery(rc, mid, r, b, e);
}
Info rangeQuery(int b, int e){
return rangeQuery(1, 0, X, b, e);
}
Info closeRangeQuery(int b, int e){
return rangeQuery(1, 0, X, b, e + 1);
}
};
struct Info{
i64 min;
Info() : min(LONG_LONG_MAX) {}
Info(i64 x) : min(x) {}
friend Info operator + (const Info& u, const Info& v) {
return Info(std::min(u.min, v.min));
}
};
int N;
std::vector<int> a;
void input(){
std::cin >> N;
a.resize(N);
for(int i = 0; i < N; i++){
std::cin >> a[i];
}
}
void interact(){
i64 sum = 0;
std::vector<i64> diff(N - 1);
for(int i = 0; i + 1 < N; i++){
diff[i] = a[i + 1] - a[i];
sum += std::abs(diff[i]);
}
// 这里只记录非边界的 i
std::set<int> peak, valley;
SegmentTree<Info> shoulder(N - 1);
auto erase = [&](int i){
// 1 <= i and i < N - 1
if(diff[i - 1] >= 0 and diff[i] <= 0){
peak.erase(i);
} else if(diff[i - 1] < 0 and diff[i] > 0){
valley.erase(i);
} else if(diff[i - 1] >= 0 and diff[i] > 0){
shoulder.modify(i, Info());
} else if(diff[i - 1] < 0 and diff[i] <= 0){
shoulder.modify(i, Info());
}
};
auto insert = [&](int i){
// 1 <= i and i < N - 1
if(diff[i - 1] >= 0 and diff[i] <= 0){
peak.insert(i);
} else if(diff[i - 1] < 0 and diff[i] > 0){
valley.insert(i);
} else if(diff[i - 1] >= 0 and diff[i] > 0){
shoulder.modify(i, std::abs(diff[i]));
} else if(diff[i - 1] < 0 and diff[i] <= 0){
shoulder.modify(i, std::abs(diff[i - 1]));
}
};
auto add_diff = [&](int p, int x){
// 1 <= p and p < N - 1
sum -= std::abs(diff[p]);
diff[p] += x;
sum += std::abs(diff[p]);
};
for(int i = 1; i + 1 < N; i++){
insert(i);
}
int Q;
std::cin >> Q;
for(int t = 0; t < Q; t++){
int op;
std::cin >> op;
if(op == 2){
// mofity
int l, r, x;
std::cin >> l >> r >> x;
--l, --r;
for(int i : {l - 1, l, r, r + 1}) if(1 <= i and i < N - 1) {
erase(i);
}
if(l - 1 >= 0) add_diff(l - 1, x);
if(r < N - 1) add_diff(r, -x);
for(int i : {l - 1, l, r, r + 1}) if(1 <= i and i < N - 1) {
insert(i);
}
} else {
// query
int l, r, x;
std::cin >> l >> r >> x;
--l, --r;
i64 ans = 0;
// 左边界
if(l == 0 and l < N - 1){
chmax(ans, sum - std::abs(diff[l]) + std::abs(diff[l] - x));
}
// 右边界
if(r == N - 1 and r - 1 >= 0){
chmax(ans, sum - std::abs(diff[r - 1]) + std::abs(diff[r - 1] + x));
}
// 峰
{
auto lb = peak.lower_bound(l);
if(lb != peak.end() and *lb <= r){
chmax(ans, sum + x * 2);
}
}
// 谷
{
auto lb = valley.lower_bound(l);
if(lb != valley.end() and *lb <= r){
int i = *lb;
assert(1 <= i and i + 1 < N);
chmax(ans, sum - std::abs(diff[i - 1]) - std::abs(diff[i]) + std::abs(diff[i - 1] + x) + std::abs(diff[i] - x));
}
}
// 平
{
i64 min = shoulder.closeRangeQuery(l, r).min;
if(min != LONG_LONG_MAX){
chmax(ans, sum + (x - min >= 0 ? 2 * x - 2 * min : 0));
}
}
std::cout << ans << "\n";
}
}
}
int main(){
std::cin.tie(0);
std::ios::sync_with_stdio(0);
input();
interact();
return 0;
}
J
https://codeforces.com/problemset/problem/297/E
分类讨论一下,发现只有,
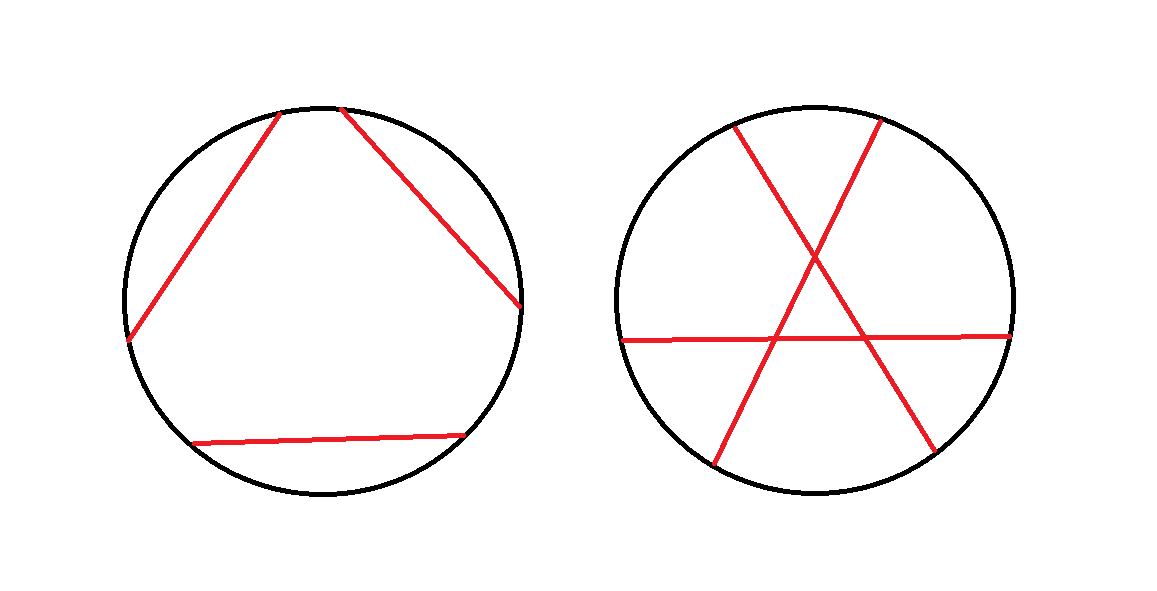
这两种位置关系能够满足题目要求。
发现求它们的方案数有点难,正难则反,我们考虑不满足关系的方案数。
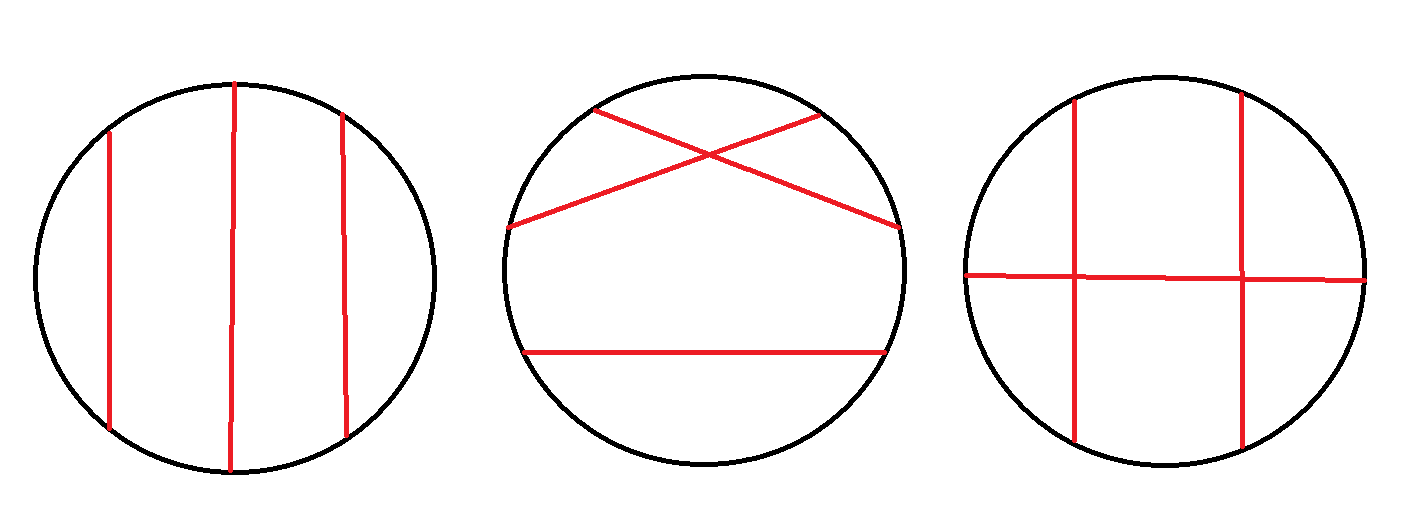
发现不满足要求的位置关系只有上面这几种(其实这就是这道题的困难所在了)。
总方案数为从 \(n\) 条弦里选出 \(3\) 条的方案数,也就是 \(C_n^3\)。
对于上面的第一张图,发现我们可以枚举每一条弦作为中间的那一条,只需要求出这条弦左右分别有多少条与它不相交的弦即可,也就是:
对于上面的第二张图以及第三张图,我们发现它们的共同点,即为三条弦中有两条弦满足其余的两条弦一条与其相交,另外一条不与其相交。方案数即为:
(因为每张图都会有两条弦满足这个条件,所以还需要除以 \(2\))。
此时我们的问题变成了如何计算 \(l_i\) 以及 \(r_i\) 。
观察一下,我们发现若一条弦 \((x'y')\) 在当前这条弦 \((xy)\) 的左边,则需要满足:
若一条弦在当前这条弦的右边,则需要满足:
使用二维偏序处理即可。
const int N = 2e5+10;
struct node{int l,r,id;}a[N];
int l[N],r[N],n,tr[N];
void add(int x,int k){for(;x<=2*n;x+=x&-x)tr[x]+=k;}
int query(int x){int res=0;for(;x;x-=x&-x)res+=tr[x];return res;}
void init(){memset(tr,0,sizeof(tr));}
inline void solve()
{
fin >> n;
for(int i = 1;i <= n;i++)
{
fin >> a[i].l >> a[i].r;
if(a[i].l > a[i].r) std::swap(a[i].l,a[i].r);
a[i].id = i;
}
std::sort(a+1,a+1+n,[](node x,node y){
return x.l < y.l;
});
for(int i = 1;i <= n;i++)
{
l[a[i].id] += query(a[i].l) + query(n*2) - query(a[i].r);
add(a[i].r,1);
}
init();
for(int i = n;i >= 1;i--)
{
r[a[i].id] += query(a[i].r) - query(a[i].l);
add(a[i].r,1);
}
std::sort(a+1,a+1+n,[](node x,node y){
return x.r > y.r;
});
init();
for(int i = 1;i <= n;i++)
{
l[a[i].id] += query(n*2)-query(a[i].r);
add(a[i].l,1);
}
int res1 = n*(n-1)*(n-2)/6,res2 = 0;
for(int i = 1;i <= n;i++)
{
res1 -= l[i]*r[i];
res2 += (l[i]+r[i]) * (n-l[i]-r[i]-1);
}
fout << res1 - res2/2 << '\n';
}
B
https://www.codechef.com/problems/SKIRES
给你一个 \(n \times m\) 的网格,以及网格上的两个格子 \(A,B\) 每个格子有一个高度,每次操作可以选择一个格子(不能是A或B)并将它的高度增加 \(1\) 你希望在 \(A,B\) 间不存在任何一条不上升路径,求最少操作次数。
这道题很容易看出来是最小割啊.
我们想一想怎么建图.
最容易想到的是两两之间连边,跑最小割,但是这个很明显是不对的.因为一个点增加了一定的值,可能对别的链有影响,所以不能怎么建图.
再来想一想,假设我们现在有一个点 \((x,y)\),四个相邻的点大于等于他.
我们将这四个点的值从小到大排一遍序
对于\(1−3\)的点,我们将他们从小编号向他自己的编号\(+1\)的点连一条流量为这个点的\(w−w[x][y]\),
对于\(4\)这个点,我们将他连向 \((x,y)\) 这个点,流量也为这个点的\(w−w[x][y]\)。
最后在将这四个点分别向自己在这四个新建节点中对应点连一条流量为\(inf\)的边。
注意要特判一下终点和起点,因为这两个点不可以增加高度。
#include<bits/stdc++.h>
#define inf 1e9
using namespace std;
typedef long long ll;
int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*f;
}
struct node{
int to,next,v;
}a[200001];
int head[100001],cnt,n,m,s,t,x,y,z,dep[100001],fx,fy,X,Y;
void add(int x,int y,int c){
a[++cnt].to=y,a[cnt].next=head[x],a[cnt].v=c,head[x]=cnt;
a[++cnt].to=x,a[cnt].next=head[y],a[cnt].v=0,head[y]=cnt;
}
queue<int> q;
int bfs(){
memset(dep,0,sizeof(dep));
q.push(s);
dep[s]=1;
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=head[now];i;i=a[i].next){
int v=a[i].to;
if(!dep[v]&&a[i].v>0)
dep[v]=dep[now]+1,q.push(v);
}
}
if(dep[t])
return 1;
return 0;
}
int dfs(int k,int list){
if(k==t||!list)
return list;
for(int i=head[k];i;i=a[i].next){
int v=a[i].to;
if(dep[v]==dep[k]+1&&a[i].v>0){
int p=dfs(v,min(list,a[i].v));
if(p){
a[i].v-=p;
if(i&1) a[i+1].v+=p;
else a[i-1].v+=p;
return p;
}
}
}
return dep[k]=0;
}
int Dinic(){
int ans=0,k;
while(bfs())
while((k=dfs(s,inf)))
ans+=k;
if(ans>=inf) return -1;
return ans;
}
int id[101][101],val[101][101],tot;
int dx[6]={0,0,0,-1,1};
int dy[6]={0,1,-1,0,0};
struct node1 {
int x,y,v;
}b[10];
bool cmp(const node1 & a , const node1 & b){
return a.v<b.v;
}
int main(){
int T=read();
while(T--){
n=read(),m=read(),s=0,t=n*m*5+1,tot=0,cnt=0;
memset(head,0,sizeof(head));
X=read(),Y=read(),fx=read(),fy=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
id[i][j]=++tot,val[i][j]=read();
add(s,id[X][Y],inf),add(id[fx][fy],t,inf);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int res=0;
for(int k=1;k<=4;k++){
int x=i+dx[k],y=j+dy[k];
if(x<1||y<1||x>n||y>m) continue;
if(val[i][j]<=val[x][y])
b[++res].x=x,b[res].y=y,b[res].v=val[x][y];
if((i==X&&j==Y)||(i==fx&&j==fy)){
if(val[i][j]>val[x][y]) add(id[x][y],id[i][j],0);
else add(id[x][y],id[i][j],inf);
}
}
if((i==X&&j==Y)||(i==fx&&j==fy)||res==0)
continue;
sort(b+1,b+1+res,cmp);
for(int k=1;k<res;k++){
int x=b[k].x,y=b[k].y,v=b[k].v;
tot++,add(tot,tot+1,v-val[i][j]+1),add(id[x][y],tot,inf);
}
tot++,add(id[b[res].x][b[res].y],tot,inf),add(tot,id[i][j],b[res].v-val[i][j]+1);
}
printf("%d\n",Dinic());
}
return 0;
}
G
https://codeforces.com/contest/1431/problem/J
我们可以将问题转化为以下形式:需要选择 n−1 个元素 \(b_i\),使得 \(a_i \leq b_i \leq a_{i+1}\),并且要求 \(b_1 \oplus b_2 \oplus \cdots \oplus b_{n-1} = a_1 \oplus a_2 \oplus \cdots \oplus a_n\)。我们可以从最高位到最低位逐位解决这个问题。
在每一位 \(pw\) 上,对于每个 \(b_i\),我们有一个可能的值区间 [l, r]。我们定义一个数 \(x\) 在第 \(pw\) 位上的值为 \(x(pw)\)。如果 \(l(pw) = r(pw)\),我们没有选择的余地,此时区间 [l, r] 不会改变。否则,\(l(pw) = 0\) 且 \(r(pw) = 1\)。
我们有两个选择:
- 如果我们选择 \(b_i(pw) = 0\),那么左边界 \(l\) 不变,但右边界 \(r\) 变为 \(2^{pw} - 1\)(实际上不是精确的 \(2^{pw} - 1\),但由于我们从高位到低位遍历,忽略掉更高的位,可以这样看待);
- 如果我们选择 \(b_i(pw) = 1\),那么右边界 \(r\) 不变,但左边界 \(l\) 变为 0(我们同样忽略掉更高位的情况)。
因此,我们可以看出,左边界 \(l\) 可能是初始的 \(a_i\),也可能是 0;右边界 \(r\) 可能是初始的 \(a_{i+1}\),也可能是 \(2^{pw} - 1\)。这就导致了一个带有 4 个状态的状压 DP。但是,即便使用了分治技巧,时间复杂度大致为 \(O(4^n \cdot n \cdot B)\),其中 \(B\) 是位数。
因此我们需要进一步考虑。
需要注意的是,如果我们遇到了状态,其中左边界是 0 且右边界是 \(2^{pw} - 1\),那么这个情况是特殊的,因为我们可以选择其他所有 \(b_j\) 的值,并用 [0, \(2^{pw} - 1\)] 中的某个数来抵消,使得所有 \(b_i\) 的异或和正好等于 \(a_1 \oplus a_2 \oplus \cdots \oplus a_n\)。因此,如果我们在至少一个 \(b_i\) 中遇到这种状态,我们可以显式地计算出答案,即除去这个特定区间外,所有区间 [l, r] 的乘积。
另一方面,如果左边界变为 0(或者右边界变为 \(2^{pw} - 1\)),那么这种状态会持续下去,状态只会在选择了相反的步骤后变为 [0, \(2^{pw} - 1\)]。例如,如果对于某个 \(b_i\),我们最初选择将其设置为 0,并遇到了 [l, \(2^{pw} - 1\)] 状态,如果之后我们继续选择 0,那么状态不会变化。只有在选择 1 后,才会遇到状态 [0, \(2^{pw} - 1\)]。
换句话说,对于每个 \(b_i\),我们可以选择:先设置若干个 0,然后再选择 1;或者先设置若干个 1,然后再选择 0。总共有 \(2^{n-1}\) 种状态。现在对于每种掩码,遍历第一个选择与掩码相反的位 \(pw\),这样在下一步就会进入特殊情况。为了计算此时的答案,我们可以为每个 \(b_i\) 找到唯一确定的区间 [l, r],并计算出 \(dp[n][2][2]\),其中 \(dp[pos][parity][flag]\) 表示在长度为 \(pos\) 的前缀中,从区间 [l, r] 选择 \(b_i\) 的方式数,并且当前的异或和为 \(parity\),并且如果某个 \(b_i(pw)\) 的选择与掩码相反,flag 为真。
对于每一位 \(pw\),其答案为:所有情况下的总和等于 \(dp[n][(a_1 \oplus a_2 \oplus \cdots \oplus a_n)(pw)][1] \cdot 2^{-pw}\)(因为我们要排除长度为 1 的区间 [0, \(2^{pw} - 1\)])。
M
https://codeforces.com/problemset/problem/917/E
假设 \(t_i\) 是 \(s_i\) 的逆序。我们使用点分治来处理这个问题。在处理子树 \(S\) 时,假设它的重心是 \(c\)。对于一个固定的查询,假设 \(v\) 和 \(u\) 都在 \(S\) 中,且从 \(v\) 到 \(u\) 的路径经过重心 \(c\)(这对于每对 \(v\) 和 \(u\) 恰好会发生一次)。假设 \(x\) 是从 \(c\) 到 \(v\) 的路径所对应的字符串,\(y\) 是从 \(c\) 到 \(u\) 的路径所对应的字符串。我们需要计算 \(s_k\) 在字符串 \(\text{reverse}(x) + y\) 中出现的次数。如果字符串 \(s\) 在 \(t\) 中出现的次数是 \(f(s, t)\),那么:
其中,前两个变量可以通过 ACAM 和线段树来计算。
A 是在路径中出现的那些情况,其中部分属于 \(\text{reverse}(x)\),部分属于 \(y\),并且它们跨越了从重心 \(c\) 到 \(v\) 和从重心 \(c\) 到 \(u\) 的路径。
到目前为止,时间复杂度是 \(O(n \log n)\)。
现在我们来计算 A,首先为每个字符串构建后缀树(对于每个 \(s_k\) 和 \(t_k\))。后缀树是一个字典树,因此,设 \(sf(v, s)\) 为当我们在字符串 \(s\) 的后缀树中查询从根到节点 \(v\) 的路径时,所到达的节点。我们可以快速计算每个 \(v\) 和字符串 \(s\) 的对应后缀树节点,只要我们在开始点分治之前将所有的后缀树合并成一个大的字典树(这个过程是预处理过程的一部分)。
我们给字典树中的每个节点关联一个值 val,初始时所有节点的值都为零。然后我们像 DFS 一样遍历字典树。当我们到达节点 \(x\) 时,我们遍历所有以节点 \(x\) 结尾的后缀(总共有 \(2^{(|s_1| + |s_2| + ... + |s_n|)}\) 个后缀),对于每个后缀(\(s, k\)),其中 \(s\) 是字符串 \(s\) 的后缀,长度为 \(k\),我们将 val 的值加 1,这个值加到所有以 \(\text{reverse}(s)\) 为后缀的节点的子树中;当我们退出节点 \(x\) 时,在 DFS 中会将这个值减去。
回到点分治中,A 等于在字典树中,当前在 DFS 遍历过程中,我们遇到的节点所对应的后缀值。具体来说,A 是指,当前遇到的节点是一个后缀树中的节点,其中包含后缀 \(t_k\) 与某个节点 \(s_k\) 的最长前缀,这个最长前缀的长度为 \(a\),并且 \(b\) 是字符串路径从重心 \(c\) 到 \(v\) 时,字符串的后缀大小。为了实现这一目标,我们可以使用主席树来维护字典树节点的时间范围,或者在不使用主席树的情况下,等到重心分解完成后再计算所有的 A,也就是离线后再计算。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号