题解:P5100 [JOI 2017 Final] 足球 / Soccer
题意简介
在二维网格平面上有 \(N\) 个球员,球最初位于第 \(1\) 个球员处。我们需要将球转移到第 \(N\) 个球员处,求所有球员疲劳度之和的最小值。
持球的球员可以选择踢球或运球,不持球的球员只能进行移动,踢球时可以从东南西北中选定一个方向将球踢出 \(p\) 米,所提升的疲劳度为 \(A \times p + B\),且球滚动时可以穿过其它球员。
运球以及移动时可以从东南西北中选定一个方向前进 \(p\) 米,所提升的疲劳度为 \(C \times p\)。
一个球员控球以及停止控球都不会对该球员的疲劳度造成影响。
前置知识
这道题是一道比较明显的分层图,我下面将会讲解什么是分层图以及分层图问题的解题思路。此外你还需要知道一种求解单源最短路问题的算法,在这里我就不阐述了。
分层图,顾名思义就是一张有很多层的图()。
每一层可以看作原图的一个“副本”,但不同层之间通过特定的边连接,这些边代表了某些特殊操作或状态转移。通过这种方式,我们可以将复杂的问题转化为在分层图上求解最短路、连通性等经典图论问题。
分层图中的每一层对应原图的一种状态或阶段,层与层之间的边代表了状态转移,即进行某种特殊操作后从当前状态进入下一状态。
- 普通操作(如原图的边)通常在同一层内连接节点。
- 特殊操作(如跳过边、反向边、改变权值等)通过跨层边实现。
例如在飞行路线一题中,每一层表示已使用的特权次数。
我们建出图来的效果就是这样的:
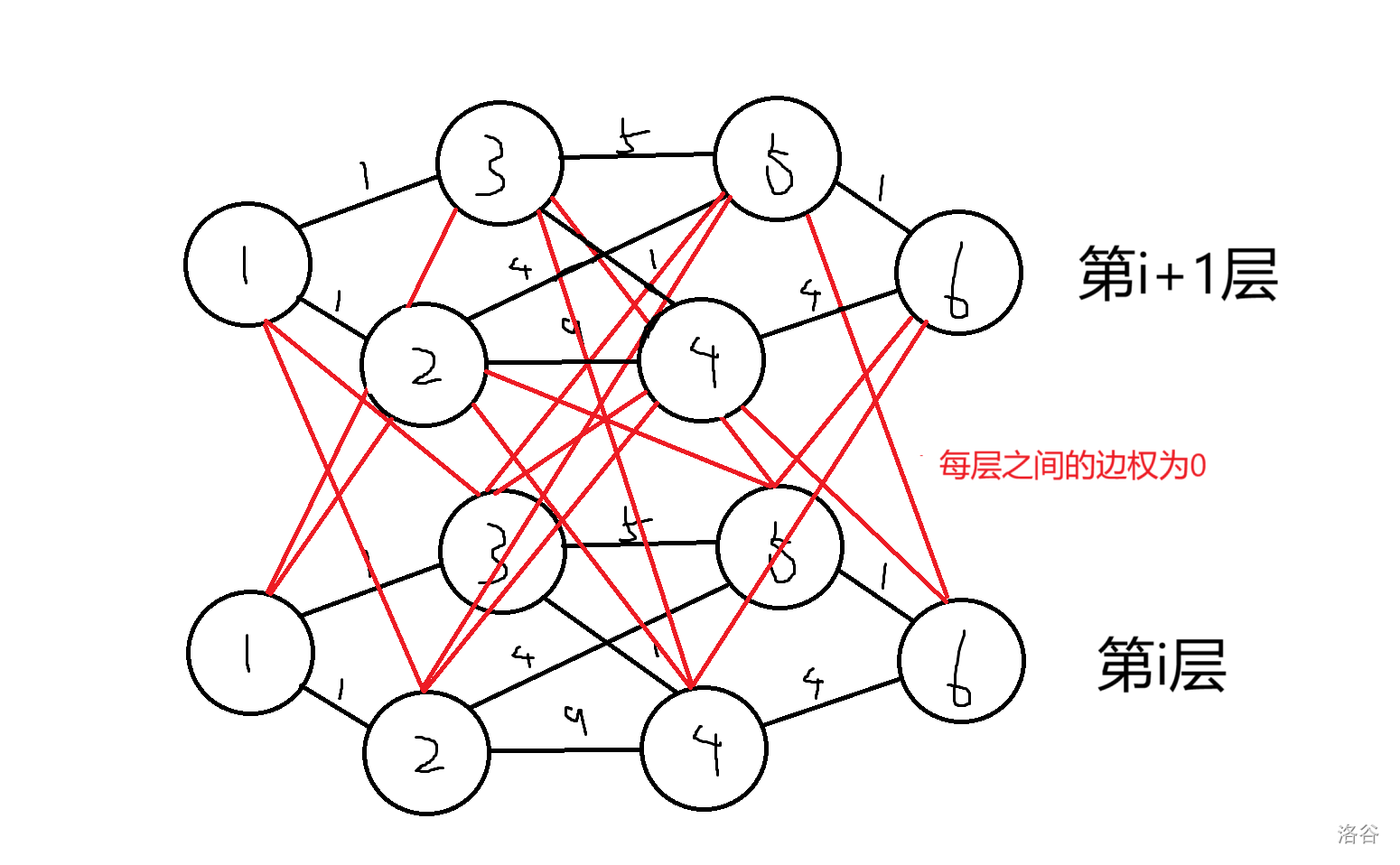
然后我们建 \(k\) 层相同的图跑最短路就好了。
相信看到这你已经明白分层图的含义以及大致思路了。
那接下来我们就步入正题吧。
解题思路
其实做这道题之前,如果你做过回家的路这道题,那你会发现这两道题在球滚动的不同方向的处理上有异曲同工之妙,我们就可以把球竖着滚动和横着滚动的状态分别建出两层图,只有球被人拦截到我们才能改变球的滚动方向。
此时我们对于这道题就有大致的思路了,建三层图,一层表示人正在运球的状态,剩下的两层表示球不同滚动方向的状态。
此外我们还需要预处理出每个点到最近球员的曼哈顿距离,因为我们每次需要让离球最近的人去捡球,一个 BFS 就可以解决了。
BFS 的代码如下。
il void bfs() {
queue<node> q;
memset(mhd, 0x3f, sizeof(mhd));
for(int i=1; i<=n; i++)
{
mhd[s[i]][t[i]] = 0;
q.push({s[i], t[i]});
}
while(!q.empty())
{
node u = q.front(); q.pop();
int x = u.x, y = u.y;
for(int k=1; k<=4; k++) {
int nx = x + dx[k], ny = y + dy[k];
if(nx<0 || nx>h || ny<0 || ny>w) continue;
if(mhd[nx][ny] > mhd[x][y] + 1)
{
mhd[nx][ny] = mhd[x][y] + 1;
q.push({nx, ny});
}
}
}
}
建图的代码如下。
il void build()
{
int mx = (w+1)*(h+1);
for(int i = 0;i <= h;i++)
for(int j = 0;j <= w;j++)
{
int u = p(i,j);
for(int k = 1;k <= 4;k++)
{
int x = i+dx[k];
int y = j+dy[k];
if(x<0||x>h||y<0||y>w) continue;
int v = p(x,y);
E[u].emplace_back(e{v,C});
}
E[u].emplace_back(e{u+mx,B});
E[u].emplace_back(e{u+mx*2,B});
}
for(int i = 0;i <= h;i++)
for(int j = 0;j <= w;j++)
{
int u = p(i,j);
for(int k = 1;k <= 2;k++)
{
int x = i+dx[k];
int y = j+dy[k];
if(x<0||x>h||y<0||y>w) continue;
int v = p(x,y);
E[u+mx].emplace_back(e{v+mx,A});
}
E[u+mx].emplace_back(e{u,mhd[i][j]*C});
for(int k = 3;k <= 4;k++)
{
int x = i+dx[k];
int y = j+dy[k];
if(x<0||x>h||y<0||y>w) continue;
int v = p(x,y);
E[u+mx*2].emplace_back(e{v+mx*2,A});
}
E[u+mx*2].emplace_back(e{u,mhd[i][j]*C});
}
}
初始时球处于第一层,结束时球也需要处于第一层,此时我们求解这两个点的最短路即可。
AC 代码
#include<bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';
#define il inline
#define Coded_By_Zheng_iii 0
using namespace std;
using ll = long long;
using ull = unsigned long long;
#define int ll//不开long long见祖宗
const int N = 1e5+10;
const int M = 510;
const int dx[] = {0,0,0,-1,1};
const int dy[] = {0,1,-1,0,0};
struct e{
int to,w;
};
struct node{
int x,y;
};
vector<e> E[M*M*4];
int n,h,w,A,B,C,s[N],t[N],mhd[M][M];
il int p(int x,int y){return x*(w+1)+y;}
il void build()
{
int mx = (w+1)*(h+1);
for(int i = 0;i <= h;i++)
for(int j = 0;j <= w;j++)
{
int u = p(i,j);
for(int k = 1;k <= 4;k++)
{
int x = i+dx[k];
int y = j+dy[k];
if(x<0||x>h||y<0||y>w) continue;
int v = p(x,y);
E[u].emplace_back(e{v,C});
}
E[u].emplace_back(e{u+mx,B});
E[u].emplace_back(e{u+mx*2,B});
}
for(int i = 0;i <= h;i++)
for(int j = 0;j <= w;j++)
{
int u = p(i,j);
for(int k = 1;k <= 2;k++)
{
int x = i+dx[k];
int y = j+dy[k];
if(x<0||x>h||y<0||y>w) continue;
int v = p(x,y);
E[u+mx].emplace_back(e{v+mx,A});
}
E[u+mx].emplace_back(e{u,mhd[i][j]*C});
for(int k = 3;k <= 4;k++)
{
int x = i+dx[k];
int y = j+dy[k];
if(x<0||x>h||y<0||y>w) continue;
int v = p(x,y);
E[u+mx*2].emplace_back(e{v+mx*2,A});
}
E[u+mx*2].emplace_back(e{u,mhd[i][j]*C});
}
}
il void bfs() {
queue<node> q;
memset(mhd, 0x3f, sizeof(mhd));
for(int i=1; i<=n; i++)
{
mhd[s[i]][t[i]] = 0;
q.push({s[i], t[i]});
}
while(!q.empty())
{
node u = q.front(); q.pop();
int x = u.x, y = u.y;
for(int k=1; k<=4; k++) {
int nx = x + dx[k], ny = y + dy[k];
if(nx<0 || nx>h || ny<0 || ny>w) continue;
if(mhd[nx][ny] > mhd[x][y] + 1)
{
mhd[nx][ny] = mhd[x][y] + 1;
q.push({nx, ny});
}
}
}
}
int dis[M*M*4];
bool vs[M*M*4];
struct pr{
int u,d;
};
priority_queue<pr> q;
il bool operator<(const pr &a,const pr &b){
return a.d > b.d;
}
il void dij(int s){
memset(dis,0x3f,sizeof(dis));
dis[s] = 0;
q.push(pr{s,dis[s]});
while(!q.empty()){
pr x = q.top();
q.pop();
int u = x.u;
if(vs[u])continue;
vs[u] = 1;
for(e ee : E[u]){
int v = ee.to;
int w = ee.w;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
q.push({v,dis[v]});
}
}
}
}
signed main(){
// freopen("test.in","r",stdin);
// freopen("test.out","w",stdout);
ios::sync_with_stdio(0),cout.tie(0),cin.tie(0);
cin>>h>>w>>A>>B>>C>>n;
for(int i = 1;i <= n;i++)
cin>>s[i]>>t[i];
bfs();//预处理曼哈顿距离
build();//建图
dij(p(s[1],t[1]));//跑最短路
cout<<dis[p(s[n],t[n])];
return Coded_By_Zheng_iii;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号