方差-Variance

Work by Jianfei is licensed under zencorn@hotmail.com Creative Commons wei 3.0 Unported License .

 

预备知识：

                    数学期望 E(x)：http://www.cnblogs.com/zencorn/archive/2011/03/24/1993690.html

 

方差：Variance US: ['veriəns]  UK: ['veəriəns] 

    在所有基于信息技术进行有效分析处理的行业最后都要借助数学工具来完成有效的问题解决和展现。 如金融行业的投资组合策略Portflio    Management， 零售业界的数据挖掘Data Mining等。方差就是期间一个基本的评估指标。

     在概率论和数理统计中，方差（英文Variance）用来度量随机变量和其数学期望（即均值）之间的偏离程度。在许多实际问题中，研究随机变量和均值之间的偏离程度有着很重要的意义。

概述　　如下面的例子：

　　已知某零件的真实长度为a，现用甲、乙两台仪器各测量10次，将测量结果X用坐标上的点表示如图：

　　甲仪器测量结果：

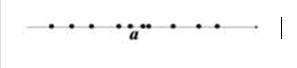
乙仪器测量结果： 

 

两台仪器的测量结果的均值都是 a 。但是用上述结果评价一下两台仪器的优劣，很明显，我们会认为乙仪器的性能更好，因为乙仪器的测量结果集中在均值附近。

由此可见,研究随机变量 X 与其均值E(X)的偏离程度是十分必要的.那么,用怎样的量去度量这个偏离程度呢?容易看到E(|X-E(X)|)能度量随机变量与其均值E(X)的偏离程度. 但由于上式带有绝对值,运算不方便,通常用量

　　E{[X-E(X)]^2} 这一数字特征就是方差。

 

 

 方差公式：

         方差是实际值与期望值之差平方的期望值，而标准差是方差平方根。

 

 则例子可以举例为测量4次： 甲；11 ， 9 ， 9， 11。

                                         乙；13 ， 8 ，12，  7。

首先对应实际值的期望值为： 10

因为四次测量所以求方差的分母为： 4

则： 甲、乙方差分别为 ：

  甲 =  [(11-10) ^2 + (9-10)^2+(9-10)^2+(11-10)^2]/4

       = [ 1+1+1+1]/4

       = 1

 乙 = [ (13-10)^2+(8-10)^2+(12-10)^2+(7-10)^2]/4

      =[ 9+4+4+9]/4

      = 26/4

结论： 甲相对乙来说具有更为稳定的测量精确值分布，次数相同的情况下平均偏差值更小。

 

 

Work by Jianfei is licensed under a Creative Commons wei 3.0 Unported License .