（四）图论

摘要

图论大概分成两个部分，建模和在图论模型上解决问题。关于前者是及其需要大家做题来积累的，可以跟着网上一些博主的做题笔记来，本文重点介绍后者和以及一些经典套路的建模。

0 图论相关概念

本文所有设计到的概念均在此处提出，如有错漏请提出。

图是一个二元组 \(G=(V,E)\)，其中 \(V\) 是一个非空集合，称作点集，\(E\) 是一个二元组集合，称作边集。\(V\) 中的每个元素，称作节点或顶点，\(E\) 中的元素是 \(V\) 中元素的二元组，也就是 \(E=\{(u,v)|u,v\in V\}\)。

若 \(E\) 中的每个二元组都是无序的，则称图 \(G\) 是无向图，否则便是有向图。如果既有序的，也有无序的，则称为混合图。记 \(u\to v\) 代表存在一条 \(u\) 到 \(v\) 的边即 \((u,v)\in E\)。如果存在 \(u\to u\)，则称这是一个自环（loop）。如果有多条 \(u\to v\) 的边，则称这是若干条重边（multiple edge）。对于一个无重边无自环的图，称作简单图。

邻域：在无向图中，\(N(u)\) 记为所有与 \(u\) 存在一条边的点集，即 \(N(u)=\{v|u\to v\}\)。一个点集的邻域即为其所有点的邻域的并 \(N(S)=\bigcup\limits_{v\in S}N(v)\)

1 图的遍历

dfs、bfs 都是 \(O(n)\) 遍历图的方式。dfs 生成树，满足非树边一定是返祖边。

P1 Bubble Cup 2019 Alpha planetary system

给定一个连通三部图，要求给每条边一个 \(\{1,2,3\}\) 的边权。要求每两个相邻的点，所有与他们相邻的边的边权和在模 \(3\) 意义下不同，给出一个方案。

题解

dfs 树还有很多性质，后续会提到。

2 拓扑排序

对一个有向无环图 \(G=(V,E)\) 进行拓扑排序，是将 \(G\) 中所有顶点排成一个线性序列，使得图中任意一对顶点 \(u\) 和 \(v\)，若边 \((u,v)\in E\)，则 \(u\) 在线性序列中出现在 \(v\) 之前。

可以用一个序列来模拟这一过程：将 \(0\) 入度点入队，每次将所有出边删去，并加入新的 \(0\) 入度点。还可以使用 dfs 的方法，每次只递归跑没跑过的。如果一个有环拓扑排序就不会遍历所有点。拓扑序是处理 DAG 的有效武器，可以把无序的点变成有序的使其有一些性质。

按照拓扑序dp

对于一个 dag，如果有一个 dp 方程是 \(dp_{v}=\sum_{(u,v)\in E}dp_u\)，那么我们可以按照其拓扑序从前往后来dp以保证所有需要算的数据都已经提前算好了。

P2 CSP-S2020 函数调用

给你 \(n\) 个数和 \(m\) 种操作，每种操作有如下三种情况：

给某个数加上 \(V\)。

给所有数乘上 \(V\)。

依次执行操作 \(C_1,C_2,...,C_k\)。

有一个长为 \(Q\) 的操作序列，依次执行这些序列，问最后每个数是什么。

\(1\le n,m,Q\le 10^5,\sum C_i\le 10^6\)。

不知道为什么我一直觉得这道题很神。首先考虑只有1,3操作，那么只需算出每个1操作被调用了几次，这个可以拓扑排序+简单dp。考虑只有2,3操作，同样可以对每个函数求出调用它会给全局乘上啥，记作 \(M_i\)，这个直接 dfs 拓扑。

然后考虑只有1,2操作，显然对于每个1操作只需记录它被乘了几倍。我们不妨从后往前做，记一个 \(Mul\) 代表目前全局乘上了多少，每个点记一个 \(A_i\) 代表它加上有多少的权值。最后答案是 \(a_i\times Mul+A_i\)。那么对于每个1操作，直接有 \(A_{P_i}+=V_{i}\times Mul\)。

考虑同时有三个操作的时候，我们还是可以求出 \(M_i\)，然后从后往前做求出 \(Mul\)。但是现在还有一个操作3，我们得求出一个 \(f_i\) 代表 \(i\) 操作可以调用到的 1 操作会乘上一个 \(f_i\) 倍，从后往前做时直接令 \(f_i+=Mul\) 即可。

然后考虑求出每个一操作真正被放大了多少倍，还是考虑拓扑排序。这时我们要倒序考虑每个点调用的函数，因为前面的会被后面的 \(M_v\) 所影响，有转移方程 \(f_v+=f_u\times sufmul\)，后者代表后缀积。

这样这道题才算真正做完。

总结一下先考虑只有部分情况怎么做，然后拓展到一般情况，发现之前的做法还可以沿用。然后对于 \(f_i\) 的处理应当想到 dp 和拓扑排序。

拓扑序跑最短路

P3 SDOI2010 大陆争霸

给出一张有向图，如果想要到达某些点先要到达另一些点，求 \(1\) 到 \(n\) 的最短时间。你可以分身。

记录最短路和最晚可以到的时间分别为 \(d,t\)，显然到这个点的时间最早为 \(\max(d,t)\)。考虑在跑最短路的时候加一个拓扑序的限制，即入度不为 \(0\) 无法入队更新别人的答案。复杂度不变。

偏序关系

对于一个集合 \(S\) 中的一些元素的偏序关系可以描述成一个 dag，对这个 dag 拓扑排序即可求出一组合法的偏序分配方案。

P4 CF1583F Defender of Childhood Dreams

给定一个有向图和整数 \(k\)，给每条边一个颜色，使得不存超过 \(k\) 条边构成的路径都是同一个颜色，求出最少的颜色数量并给出构造。

这种题先猜结论，发现是 \(\lceil(\log_{k}{n})\rceil\)。考虑求出原图的一组拓扑排序，然后按拓扑序每 \(k\) 个点一组，每个 \(k\) 个组一大组这样一直分下去，每一层都连一种颜色的边，就构造完了。按拓扑序可以保证这些点大概是连在一起的（不是说明都不连通）。

P5 CF1385E

给定一个图，其中一些边已经定向，你要给剩下的边定向使图不存在环。

对只包含有向边的图拓扑排序，从排在前面的点向排在后面的连边。

树

树是最特殊的图，通过研究树的一些性质可以发现图的性质。树是有 \(n\) 个点 \(n-1\) 条边的简单连通图。如果是有向图，则分为内向树和外向树。

树的遍历

dfs，bfs，两种欧拉序。

P6 NOI2013 树的计数

现给定一个 DFS 序和 BFS 序，我们想要知道，符合条件的有根树中，树的高度的期望。\(2\le n\le 2\times 10^5\).

显然树高就是给 BFS 序分段，不妨设 BFS 是 \(1,2,3,\dots,n\)，考虑什么位置可以分段。

如果 \(dfn_x>dfn_{x+1}\) 那么 \(x\) 应该在 \(x+1\) 的上一层，必须分。
否则我们不能确定。

对于 DFS 相邻的两点 \(dfn_x+1=dfn_y\)，如果 \(x<y-1\)，那么一定这一段的节点深度差不超过 \(1\)。而且这个贡献在之前已经被算过了，所以这一段都不能再贡献了。这样就得到了一个充要条件。

[SDOI2015] 寻宝游戏

给定一棵树，并且给树上若干节点打上标记，求出最小的联通块包含所有有标记的点。

结论：按 dfs 序排序后，相邻两个点的 \(dis\) 的和即为最小的，通过调整法可以证明。维护的时候可以用线段树也可以用 std::set，具体来讲，用线段树维护只需要维护相邻点的距离和即可。

直径

定义：树上最远点对。

求法一，两次dfs，从随便一个点dfs找到最远的点 \(s\)，再从最远的点 dfs 找到对于这个点最远的点 \(t\)，则 \(s,t\) 是树的直径。

求法二，动态规划，记 \(mx_u,smx_u\) 分别代表 \(u\) 不同子树里最深和次深的点，合并即可。

性质两个点集并集的直径，在两个点点集分别的直径的四个点中选。

证明简单分类讨论即可。假设存在第五个点 \(e\)，如果 \(ae\) 比 \(ac,ad\) 都长，则 \(ce,de\) 中的一个会比 \(cd\) 长。

APIO2010 巡逻

题面比较长，大家可以自行阅读。这里当 \(k=1\) 的时候，就是直接找到直径然后连起来。如果可以再多一条边，分成两种情况：第一种是和原先的环无重边，这个时候直接删掉环再去求一个直径就好了。否则的话两个环重复的部分就要走两遍，把直径上的边长赋值成 \(-1\) 即可。

CF911F Tree Destruction

给你一棵 \(n\) 个结点组成的树，你需要对树进行 \(n-1\) 次操作，一次操作包含如下的步骤：

选择两个叶子结点

将这两个结点之间简单路径的长度加到答案中

从树上删去两个叶子结点之一

初始答案为 \(0\)，显然在 \(n-1\) 次操作之后树上只剩下一个结点。计算最大的答案，并构造一组操作序列。

对于一个叶子，肯定是选最远的一个叶子然后删掉这个最优，而这个最远的叶子一定是直径端点，所以我们把直径保留下来即可。最后把直径删掉就好。

树的重心

[CSP-S2019] 树的重心

小简单正在学习离散数学，今天的内容是图论基础，在课上他做了如下两条笔记：

一个大小为 \(n\) 的树由 \(n\) 个结点与 \(n - 1\) 条无向边构成，且满足任意两个结点间有且仅有一条简单路径。在树中删去一个结点及与它关联的边，树将分裂为若干个子树；而在树中删去一条边（保留关联结点，下同），树将分裂为恰好两个子树。

对于一个大小为 \(n\) 的树与任意一个树中结点 \(c\)，称 \(c\) 是该树的重心当且仅当在树中删去 \(c\) 及与它关联的边后，分裂出的所有子树的大小均不超过 \(\lfloor \frac{n}{2} \rfloor\)（其中 \(\lfloor x \rfloor\) 是下取整函数）。对于包含至少一个结点的树，它的重心只可能有 1 或 2 个。

课后老师给出了一个大小为 \(n\) 的树 \(S\)，树中结点从 \(1 \sim n\) 编号。小简单的课后作业是求出 \(S\) 单独删去每条边后，分裂出的两个子树的重心编号和之和。

我们想要求以 \(x\) 为根的子树的重心，首先有个引理：这个重心一定在以 \(x\) 开头的这条重链上（这里就是轻重链剖分中的重链）。

这其实蛮好理解的，如果 \(x\) 不是重心，则只有其重儿子才有可能是重心，同理只有其重儿子的重儿子才有可能是重心，所以重心一定在重链上。

重心一定有且最多有两个，所以我们在重链上找一个最深的点 \(y\) 使得 \(n-sz[y] \le \frac{n}{2}\)，这个点有可能成为重心。

重心的另一个性质是如果两点是重心则其一定相连。这样我们只需判断 \(y\) 和 \(father[y]\) 是不是重心即可。

怎么找到 \(y\)？我们发现在重链上倍增就行，类似倍增求 lca。怎么维护众多数组？换根就行。

AGC018D

有一颗 \(N\) 个顶点的树，顶点依次标号 \(1\sim N\)。第 \(i\) 条边连接着顶点\(A_i\)和\(B_i\)，且第 \(i\) 条边的长度为 \(C_i\)。有一张 \(N\) 个点的完全图，图上两点之间的边的边权为它们在树上的距离。求最长哈密顿路径（即不重不漏恰好经过每个点一次）。

最好的方式，肯定是对于每一条边，左右两边来回都能走。这个理论上界，在求回路的时候是可以达到的。这个可以通过调整法证明。然后对于不是回路的情况，相当于我们需要减去一条路径，并且这条路径还需要被包含在一个解当中。

事实上，所有可能的路径都经过了重心（也可以调整证明），那么找到经过重心的最短路径即可。如果有两个重心那么都需要经过。

树的重心和树上分治有很大的联系，有关树分治的内容，归到了数据结构之中，可以在数据结构中学习。

树哈希

[NOI2022] 挑战 NPC Ⅱ

虚树

最短路

题目链接

它只能反向一条边，所以我们不妨枚举一下这是哪一条边.

我们考虑反向这条边可能形成的三种情况（其实是四种）：

1、\(1 \rightarrow n\) 走最短路，\(n \rightarrow v_i \rightarrow u_i \rightarrow 1\)，即必经 \(v_i \rightarrow u_i\) 的最短路.

2、\(n \rightarrow 1\) 走最短路，\(1 \rightarrow v_i \rightarrow u_i \rightarrow n\)，即必经 \(v_i \rightarrow u_i\) 的最短路.

3、\(1 \rightarrow v_i \rightarrow u_i \rightarrow n\)，\(n \rightarrow v_i \rightarrow u_i \rightarrow 1\)，即两种都走必经 \(v_i \rightarrow u_i\).

注意前三种都要加 \(d_i\).

4、\(1 \rightarrow n\) 和 \(n \rightarrow 1\) 都走最短路（这种提前判断就好了）.

那怎么求出必经某条边的最短路呢？其实很简单，记录一下 \(1\) 到所有点，\(n\) 到所有点，所有点到 \(1\)，所有点到 \(n\) 的最短路，跑四遍dij，后两个在反图上跑（当然你也可以floyd）。

设 \(dis(i,j)\) 为 \(i \rightarrow j\) 的最短路，则必经第一种 \(v_i \rightarrow u_i\) 的最短路即为 \(dis(n,v_i)+len(v_i,u_i)+d(u_i,1)\).

可是这样子是错的，当然对于子任务2这样子是对的。

我们来思考为什么是错的，为什么子任务2又是对的呢？

原因是我们反向了某条边后如果这条边在原先最短的必经路径上的话原先的最短路就不存在了，而子任务2每条边都有一条与之相同的重边就不会影响最短路。

我们考虑必经边有多少条，我们可以处理出最短路径树，而必经边一定在树上，树边最多有 \(n\) 条，那么如果是树边就暴力重跑一遍暴力就好了（就是子任务1的暴力）。

这题代码实现其实还有点小难，这里就讲一下实现细节吧。

首先我们先把原图建出来，跑一遍 \(1 \rightarrow n\) 和 \(n \rightarrow 1\) 的最短路，并把最短路树建出来。这里就记录一下节点 \(x\) 是从哪个节点扩展来的就行了，然后把所有树边打上标记。计算出我上面讲的四个数组，当然后两个建反图即可。枚举每一条边，如果这条边是树边就把原来的边删掉从新建图，建的时候就这一条边反向，其它正常，然后跑最短路。否则也按我上面所说的三种情况扩展。

这样做貌似常数挺小的，直接跑到loj最优解第一页。评测记录及代码.

这份代码有点小问题，注意初始化的时候你的 \(inf \times 4\) 不能炸longlong否则判 \(-1\) 时就有问题。

可是这样不是最优的，因为树边不一定是必经边，所以我们每个必经边才暴力，看一眼学长写的代码.

还有个学长用了不知道什么的办法（可能是底层优化）跑到了最优解第2。我一看第一页有4个是我们机房的/jk.

写了挺久的给个赞吧。

同余最短路其实是一种优化最短路建图的方法。

通常是解决给定m个整数，求这m个整数能拼凑出多少的其他整数(这m个整数可以重复取)或给定m个整数，求这m个整数不能拼凑出的最小（最大）的整数。

我们通过一道例题来讲解。

P3403 跳楼机

简化一下题意：用a，b，c（这里用a，b，c来代替x，y，z）三个数能组成几个小于h的整数。\(h \leq 2^{63}-1\)

因为h过大所以直接建图显然是不行的，我们要优化空间。

我们因为这个跳的顺序是无关的，所以每个数都可以由若干次b/c再加上若干次a而形成的。

根据带余除法我们知道所有的整数数都可以写成ax+r的形式，其中a是除数，x是商而r是余数。

我们求出通过b/c操作能到达的最小的mod a余数是r的数，然后用一些算法即可求出能到达多少小于h的整数（到时再讲）。

这时我们同余最短路就该排上用场了。这个最小即可表示成最短路。

我们可以让a来做这个除数（其实应该用最小的最优），则r属于\([0,a-1]\)。

我们要求出所有到达所有r的最小值。所以对于每个r建立一个点。

它可以通过b，c到其它的数（点），所以我们对于每个点u连一条到v=(u+(b/c))%a的边，长度为(b/c)。

现在从0开始跑最短路即可（初始化dis[0]=0）。

设余数r的最短路为dis[r]，则可以到\(\frac{h-dis[r]}{a}+1\)个整数，统计答案。

#include <bits/stdc++.h>
using namespace std;
const long long MAXA = 1e5 + 10; 
struct node{
    long long pre, to, val;
}edge[MAXA * 20];
long long head[MAXA], tot;
long long n, h;
long long a[20];
long long dis[MAXA], vis[MAXA];
queue<long long> q;
void add(long long u, long long v, long long l) {
    edge[++tot] = node{head[u], v, l};
    head[u] = tot;
}
void spfa() {
    memset(dis, 0x3f, sizeof(dis));
    dis[0] = 0;
    vis[0] = 1;
    q.push(0);
    while (!q.empty()) {
        long long x = q.front(); q.pop();
        for (long long i = head[x]; i; i = edge[i].pre) {
            long long y = edge[i].to;
            if (dis[y] > dis[x] + edge[i].val) {
                dis[y] = dis[x] + edge[i].val;
                if (!vis[y]) {
                    vis[y] = 1;
                    q.push(y);
                }
            }
        }
        vis[x] = 0;
    }
}
long long solve(long long x) {
    long long ret = 0;
    for (long long i = 0; i < a[1]; i++) {
        if (dis[i] <= x) {
            ret += (x - dis[i]) / a[1] + 1;
        }
    }
    return ret;
}
int main() {
    n = 3;
    cin >> h;
    for (long long i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (long long i = 0; i < a[1]; i++) {
        for (long long j = 2; j <= n; j++) {
            add(i, (i + a[j]) % a[1], a[j]);
        }
    }
    spfa();
    cout << solve(h - 1);//他刚开始在1楼所以要-1
    return 0;
}

习题：

[国家集训队]墨墨的等式

这题其实就是例题的强化版，还是以最小的a[i]为除数做与例题相同的建模方法即可。

#include <bits/stdc++.h>
using namespace std;
const long long MAXA = 5e5 + 10; 
struct node{
    long long pre, to, val;
}edge[MAXA * 20];
long long head[MAXA], tot;
long long n, bmi, bmx;
long long a[20];
long long dis[MAXA], vis[MAXA];
queue<long long> q;
void add(long long u, long long v, long long l) {
    edge[++tot] = node{head[u], v, l};
    head[u] = tot;
}
void spfa() {
    memset(dis, 0x3f, sizeof(dis));
    dis[0] = 0;
    vis[0] = 1;
    q.push(0);
    while (!q.empty()) {
        long long x = q.front(); q.pop();
        for (long long i = head[x]; i; i = edge[i].pre) {
            long long y = edge[i].to;
            if (dis[y] > dis[x] + edge[i].val) {
                dis[y] = dis[x] + edge[i].val;
                if (!vis[y]) {
                    vis[y] = 1;
                    q.push(y);
                }
            }
        }
        vis[x] = 0;
    }
}
long long solve(long long x) {
    long long ret = 0;
    for (long long i = 0; i < a[1]; i++) {
        if (dis[i] <= x) {
            ret += (x - dis[i]) / a[1] + 1;
        }
    }
    return ret;
}
int main() {
    cin >> n >> bmi >> bmx;
    for (long long i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (long long i = 0; i < a[1]; i++) {
        for (long long j = 2; j <= n; j++) {
            add(i, (i + a[j]) % a[1], a[j]);
        }
    }
    spfa();
    cout << solve(bmx) - solve(bmi - 1);
    return 0;
}

最小生成树

boruvka 算法

用来解决边权互不相同的最小生成树，主要用途边数在 \(O(n^2)\) 级别的题目中。

维护一个森林，对于每棵树处理一条最小边连向其他树，每次操作合并连起来的树。注意到，这样一定不可能成环，且最多会进行 \(O(\log |V|)\) 轮。

CF1305G

图的连通性

前置芝士：

dfs，强连通分量

一般的k-sat问题就是给你n个变量\(a_i\)，每个变量有k个取值，然后给你一堆条件让你求出满足所有条件的一组解。

而当k>2时已经被证明为NP完全问题，没有多项式复杂度的解法（只能暴搜），故我们只考虑2-sat问题。

2-sat问题就是每个变量只有两种取值（当做0和1），每次给你一个条件，形如若p则q，让你求一组满足所有条件的解。

我们可以把这种条件转换到dag上。

从p连向q一条边，这时如果从x能到y则说明可以从x推出y。

注意上述条件还包含其逆否命题：若非q则非p，题目有的时候并不会给你，所以你得加上。

求解2-sat问题有多种办法，其中一种是暴搜。

就是直接看看能不能从x推出非x或从非x推出x，然后去给x定取值。

暴搜模板题：P3007 [USACO11JAN]The Continental Cowngress G

我们只要枚举每个值是0还是1，然后看看能不能推出矛盾，若都不能，则答案是？。

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 2010;
const int M = 8010;
struct node{
    int pre, to;
}edge[M];
int head[N], tot;
int n, m;
int ans[N];//0: No 1: Yes 2: ? 
int mark[N];
void add(int u, int v) {
    edge[++tot] = node{head[u], v};
    head[u] = tot;
}
void dfs(int x) {
    mark[x] = true;
    for (int i = head[x], y; i; i = edge[i].pre) if (!mark[y = edge[i].to]) dfs(y);
}
bool check(int x) {
    for (int i = 1; i <= n << 1; i++) mark[i] = 0;
    dfs(x);
    for (int i = 1; i <= n; i++) if (mark[i] && mark[i + n]) return false;
    return true;
}
bool solve() {
    for (int i = 1; i <= n; i++) {
        bool c1 = check(i);
        bool c2 = check(i + n);
        if (c1 && c2) ans[i] = 2;
        else if (c1 && !c2) ans[i] = 1;
        else if (!c1 && c2) ans[i] = 0;
        else return false;
    }
    return true;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, a, b, x, y; i <= m; i++) {
        char c, d;
        scanf("%d %c %d %c", &a, &c, &b, &d);
        x = (c == 'Y' ? 1 : 0);
        y = (d == 'Y' ? 1 : 0);
        //u: true; u + n: false
        add(a + n * (x & 1), b + n * (y ^ 1));
        add(b + n * (y & 1), a + n * (x ^ 1));
    }
    if (solve()) for (int i = 1; i <= n; i++) printf("%c", ((ans[i] < 2) ? ((ans[i] == 0) ? 'N' : 'Y') : '?'));
    else puts("IMPOSSIBLE");
    return 0;
}

时间复杂度是\(O(n(n+m))\)

还有一种做法就是tarjan求scc。

若x和非x在同一个scc里，则无论选x还是非x都会推出矛盾，显然无解。

如果x和非x不再同一个scc中，则选拓扑序较大的一个，这样保证不会推出矛盾。

注意scc缩点的颜色编号是反拓扑序，我们可以利用它，即选scc编号较小的一个。

模板题：【模板】2-SAT 问题

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1000010 << 1;
const int M = 1000010 << 1;
struct node{
    int pre, to;
}edge[M];
int head[N], tot;
int n, m;
int dfn[N], low[N], col[N], dep, c, stk[N], top, vis[N];
void tarjan(int x, int fa) {
    dfn[x] = low[x] = ++dep;
    stk[++top] = x;
    vis[x] = 1;
    for (int i = head[x]; i; i = edge[i].pre) {
        int y = edge[i].to;
        if (y == fa) continue;
        if (!dfn[y]) {
            tarjan(y, x);
            low[x] = min(low[x], low[y]);
        } else if (vis[y]) {
            low[x] = min(low[x], dfn[y]);
        }
    }
    if (dfn[x] == low[x]) {
        ++c;
        col[x] = c;
        vis[x] = 0;
        while (stk[top] != x) {
            col[stk[top]] = c;
            vis[stk[top]] = 0;
            top--;
        }
        top--;
    }
}
void add(int u, int v) {
    edge[++tot] = node{head[u], v};
    head[u] = tot;
}
int read() {
    int ret = 0, f = 1;
    char ch = getchar();
    while ('0' > ch || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while ('0' <= ch && ch <= '9') {
        ret = (ret << 1) + (ret << 3) + ch - '0';
        ch = getchar();
    }
    return ret * f;
}
int main() {
    n = read();
    m = read();
    for (int k = 1; k <= m; k++) {
        int i, j, a, b;
        i = read();
        a = read();
        j = read();
        b = read();
        //i: true; i + n: false 
        add(i + (a & 1) * n, j + (b ^ 1) * n);
        add(j + (b & 1) * n, i + (a ^ 1) * n);
    }
    for (int i = 1; i <= n << 1; i++) {
        if (!dfn[i]) {
            tarjan(i, 0);
        }
    }
    bool ans = 1;
    for (int i = 1; i <= n; i++) {
        if (col[i] == col[i + n]) {
            ans = 0;
        }
    }
    if (ans) {
        puts("POSSIBLE");
        for (int i = 1; i <= n; i++) {
            printf("%d ", col[i] < col[i + n]);
        }
    } else {
        puts("IMPOSSIBLE");
    }
    return 0;
}

练习题：

满汉全席（模板题，JS省选竟然出模板！）

和平委员会（有时模板，POI也放模板）

[NOI2017]游戏（稍微有点思维难度的模板。）

匹配和网络流

几类特殊图模型

竞赛图

定义把 \(n\) 个点，\(\dfrac{n(n-1)}{2}\) 条边的有向完全图称作竞赛图。

性质 1（兰道定理）：

图 \(G\) 是竞赛图的充要条件是，将所有点的出度从小到大排序，记得到的序列为 \(\{d_i\}\)，其前缀和数组为 \(s_i=\sum\limits_{k=1}^{i}d_k\)，那么有 \(\forall k\in[1,n],s_k\ge \binom{k}{2}\)，且 \(k=n\) 时取等.

证明：

（1）由于竞赛图是完全图，所以必要性显然（任意一个竞赛图都满足兰道定理）.

（2）考虑一个序列满足兰道定理，

推论 1

如果 \(x\) 的出度大于 \(y\) 的出度，则存在 \(x\leadsto y\) 的路径。反证法，如果不存在则 \(y\) 在 \(x\) 拓扑序之前，此时不可能有 \(d_x>d_y\)。

性质 2 缩点

竞赛图强连通缩点之后是一条链（的形式）。证明可以用反证法：假设不存在一条链，而整张图又弱连通，所以缩完点后存在边 \(x\to z,y\to z\)。由于是竞赛图，\(x,y\) 之间一定存在有向边，所以 \(x,y,z\) 可以重新缩点或者形成一条链。

推论 2 强连通分量计数

结合性质 1&2，可得对于 \(s_k=\binom{k}{2}\) 的 \(k\)，构成一个强连通分量的断点。所有强连通分量的点一定是度数大小相邻的，而强连通分量的个数就是 \(\sum_{k=1}^{n}[s_k=\binom{k}{2}]\)。

性质 3 哈密顿路

（Redei 定理&Camion-Moon）竞赛图一定存在一条哈密顿路径，强连通的竞赛图一定存在一条哈密顿回路。

下面有一个 \(O(n^2)\) 的构造方法。

首先构造哈密顿通路，考虑增量构造。

假设我已经求出前 \(i-1\) 个点的一个哈密顿通路，考虑将 \(i\) 加入。设前面的哈密顿通路起点为 \(s\) 终点为 \(t\)，每个点 \(x\) 下一个点为 \(nxt_x\)。如果 \(t\to i\) 或者 \(i\to s\) 那么直接将 \(i\) 加入这条链即可，将 \(t\) 或 \(s\) 设成 \(i\)。

否则一定是下面这样：

那么显然一定存在一个 \(x\) 使得 \(x\to i,i\to nxt_x\)。将 \(i\) 插到 \(x,nxt_x\) 之间，即令 \(nxt_i=nxt_x,nxt_x=i\) 即可。

至此我们完成了哈密顿通路的构造。时间复杂度 \(O(n^2)\)。

之后考虑强连通竞赛图的哈密顿回路，首先求出哈密顿通路，还是设起点为 \(s\)，终点为 \(t\)。

考虑找到第一个 \(x\) 使得 \(x\to s\)，也就是第一可以成环的位置，设为新的 \(t\)。现在得到了一个环 \(s-> nxt_s-> \dots -> t-> s\)。这里我们不把 \(t-> s\) 这条边显示出来，也就是说 \(nxt_t\) 还是哈密顿通路上的下一个点。另外由于这个图是强连通的，所以一定可以找到这样一个 \(x\)。

然后考虑加入 \(nxt_t\)，还是设为 \(i\)。

如果 \(i\to s\)，那么直接扩展即可。否则我们直接找到第一个 \(x\) 使得 \(i\to x\)，那么我们可以简单地构造出下面这样的路径：

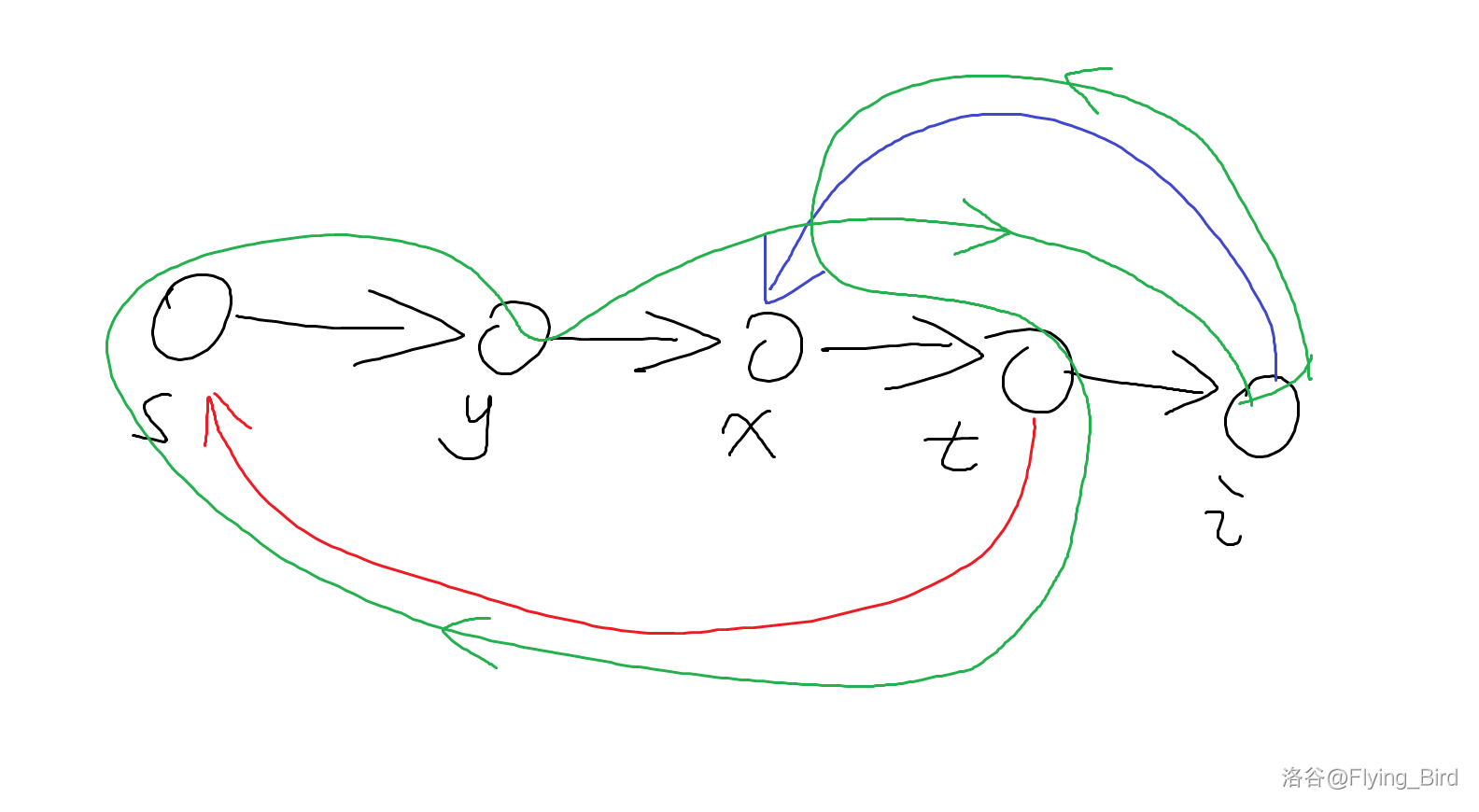
即设 \(x\) 的前一个是 \(y\)，那么构造 \(i-> x-> \dots->t-> s-> \dots-> y->i\)。此时为了保证 \(nxt_t\) 还是哈密顿通路上的点，我们令 \(s=t,t=i\)，修改 \(nxt_s\) 为原来的 \(s\)，\(nxt_y\) 为 \(i\) 即可。由于 \(x\) 是第一个 \(i\to x\)，所以一定有 \(y\to i\)。

如果压根找不到 \(x\) 呢？仔细想想发现确实有这种情况，因为只有后继节点有一个连向前面那么就保证了强连通的性质。既然如此，那这些点不如直接摆烂，让后面那个点去往前连，如下图：

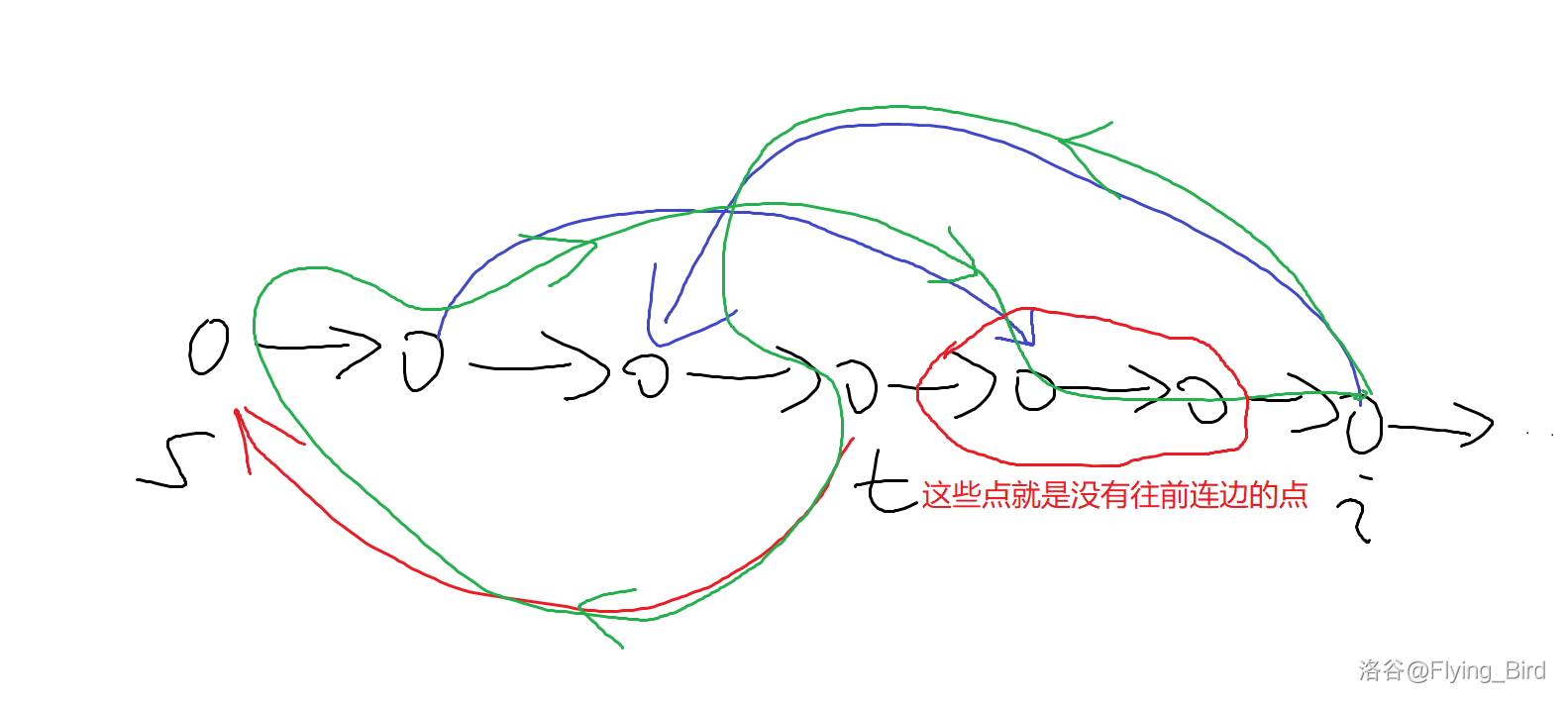
即 \(i->x->\dots ->t->s->\dots->y->nxt_t->\dots->i\)。注意这里这里 \(nxt_t\) 即 \(t\) 在哈密顿通路中的下一个点，即图中圆圈中最左边的点。然后和上面类似，只需把 \(nxt_y=i\) 修改为 \(nxt_y=nxt_t\)，这里 \(t\) 是原来的终点。注意由于红圈中的点没有向前面连边，那么前面的每个点都会向其中的点连边，所以一定有 \(y\to nxt_t\)。

然后这样一直跑，由于强连通，所以 \(x\) 最后一定存在，所以一定会求出一条哈密顿回路其中的一条链，其中起点是 \(s\)，终点是 \(t\) 且存在 \(t\to s\) 的边。

容易发现这个流程的复杂度为 \(O(n^2)\)。

推论 3（Camion-Moon 定理推论）

竞赛图的 \(k\ge 3\) 个点的SCC中一定存在 \([3,k]\) 元环。根据上述增量构造可证。

例【集训队作业2018】世界是个动物园

例竞赛图最小割

例 CTT2020 Day2 C 基础图论练习题

例 CF1268D Invertation in Tournament

例 CF1338E JYPnation

posted @ 2025-06-08 20:05 Semsue 阅读(54) 评论(0) 收藏举报

刷新页面返回顶部

Loading

Semsue(Gemini)