2022杭电第一场
B Dragon slayer
起始坐标和终点坐标带小数,需要转化为整数来处理()
二进制枚举嗯搜就完了
点击查看代码
#include<iostream>
#include<cstring>
using namespace std;
int n, m, k;
int xs, ys, xt, yt;
int wall;
int x1[16], y1[16], x2[16], y2[16];
bool p[16], col[40][40];
const int dx[4] = {0, 2, 0, -2};
const int dy[4] = {2, 0, -2, 0};
bool valid(int x, int y)
{
return x >= n or x < 0 or y < 0 or y >= m or col[x][y];
}
void dfs(int x, int y)
{
col[x][y] = 1;
for (int i = 0; i < 4; i++)
{
int newx = x + dx[i];
int newy = y + dy[i];
int midx = x + dx[i] / 2;
int midy = y + dy[i] / 2;
if (valid(newx, newy))continue;
bool fa = 0;
for (int j = 0; j < k; j++)
{
if (!(wall >> j & 1))continue;
if (x1[j] == x2[j])
{
if (midx == x1[j] and midy >= y1[j] and midy <= y2[j])
{
fa = 1;
break;
}
}
else
{
if (midy == y1[j] and midx >= x1[j] and midx <= x2[j])
{
fa = 1;
break;
}
}
}
if (!fa)dfs(newx, newy);
}
return;
}
int cnt(int x)
{
int ans = 0;
while (x)
{
if (x & 1)ans++;
x >>= 1;
}
return ans;
}
int fd()
{
int ans = k, tn = 1 << k;
for (int i = 0; i < tn; i++)
{
if (k - cnt(i) > ans)continue;
memset(col, 0, sizeof col);
wall = i;
dfs(xs, ys);
if (col[xt][yt])
{
if (k - cnt(i) < ans)ans = k - cnt(i);
}
}
return ans;
}
void slove()
{
cin >> n >> m >> k;
cin >> xs >> ys >> xt >> yt;
n *= 2;
m *= 2;
xs = xs * 2 + 1;
ys = ys * 2 + 1;
xt = xt * 2 + 1;
yt = yt * 2 + 1;
for (int i = 0; i < k; i++)
{
cin >> x1[i] >> y1[i] >> x2[i] >> y2[i];
x1[i] *= 2;
x2[i] *= 2;
y1[i] *= 2;
y2[i] *= 2;
if (x1[i] > x2[i])swap(x1[i], x2[i]);
if (y1[i] > y2[i])swap(y1[i], y2[i]);
}
cout << fd() << endl;
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
slove();
}
return 0;
}
C backpack
求恰好装满背包的时候, 异或值最大值。
使用bitset来优化(bitset尽量不要开太大 不然每次清理的时候耗时比较长 会t)
转移方程为
点击查看代码
#include<bits/stdc++.h>
#define IO std::ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
using namespace std;
const int N = 1030;
bitset<N> f[N], g[N];
int n, m;
void slove()
{
cin >> n >> m;
f[0][0] = 1;
for (int i = 1; i <= n; i++)
{
int v, w;
cin >> v >> w;
for (int j = 0; j < 1024; j++)
{
g[j] = f[j];
g[j] <<= v;
}
for (int j = 0; j < 1024; j++)
{
f[j] |= g[j ^ w];
}
}
int ans = -1;
for (int j = 0; j < 1024; j++)
{
if (f[j][m])
{
ans = j;
}
}
cout << ans << '\n';
for (int i = 0; i <= 1024; i++)
{
f[i].reset();
g[i].reset();
}
}
int main()
{
IO
int _T;
cin >> _T;
while (_T--)
{
slove();
}
return 0;
}
D Ball
题目大意
给你\(n\)个点,问有多少三元组满足距离的中位数为质数(保证没有重合的点)
数据范围
\(1\leq N\leq 2000,1\leq M \leq 10^{5},1\leq x_i,y_i \leq M\)
思路
先筛质数,范围只有\(2\times 10^5\),先暴力求解每两个点之间的距离,然后枚举中位数距离,因为不会重所以可以使用\(bitset\)来维护贡献
\(f[x][k]\land f[k][y] = 1\)表示满足条件
对于答案的贡献为
计算完贡献之后需要更新\(f[x][y] = f[y][x] = 1\)
点击查看代码
#include<bits/stdc++.h>
#define IO std::ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
const int N = 2e3 + 10, M = 2e6 + 10;
using namespace std;
struct Edge
{
int u, v, w;
bool operator < (const Edge &a)const
{
return w < a.w;
}
} e[M];
struct Point
{
int x, y;
} p[N];
bitset<N> f[N];
bool vis[M];
int pri[M], cnt;
void init(int n)
{
vis[1] = 1;
for (int i = 2; i <= n; i++)
{
if (!vis[i])
{
pri[++cnt] = i;
}
for (int j = 1; j <= cnt and pri[j] <= n / i; j++)
{
int cur = pri[j];
vis[cur * i] = 1;
if (!(i % cur))break;
}
}
}
int n, m;
int cal(int x, int y)
{
return abs(p[x].x - p[y].x) + abs(p[x].y - p[y].y);
}
void slove()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
f[i].reset();
}
for (int i = 1; i <= n; i++)
{
cin >> p[i].x >> p[i].y;
}
int cnt = 0;
for (int i = 1; i <= n; i++)
{
for (int j = i + 1; j <= n; j++)
{
e[++cnt] = {i, j, cal(i, j)};
}
}
sort(e + 1, e + 1 + cnt);
long long ans = 0;
for (int i = 1; i <= cnt; i++)
{
int x = e[i].u, y = e[i].v, w = e[i].w;
if (!vis[w])
{
ans += (f[x] ^ f[y]).count();
}
f[x][y] = f[y][x] = 1;
}
cout << ans << '\n';
}
int main()
{
IO
int _T = 1;
cin >> _T;
init(2e5+10);
while (_T--)
{
slove();
}
return (0 - 0);
}
H path
题目大意
\(n\)个点,\(m\)条边,\(s\)为起始点.边有普通边和特殊边,经过特殊边之后,到达与其不相邻的点可以免费传送,相邻的点花费会变为\(w_i - k(0\leq w_i-k)\),求解最短路,
数据范围
\(1\leq \sum m,\sum n \leq 10^6,1\leq x,y,S\leq n,1\leq w,K \leq 10^9\)
\(K\leq w_i(1\leq i\leq m)\)
思路
建立分层图\(dis[i][0]\),普通边 也就是普通最短偶\(dis[i][1]\),特殊边,用\(set\)维护,优先选择不相邻的点(因为花费最低),若要是去邻点的话就要将边权减去\(K\)
点击查看代码
/**
*
* @file Path
* @link http://acm.hdu.edu.cn/showproblem.php?pid=7145
* @author: liyajun
* @date: 2022-07-27 15:41:00
*
**/
#include<bits/stdc++.h>
#define IO std::ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
#define int long long
const int N = 1e6 + 10, INF = 1e18;
using namespace std;
int n, m, s, k;
int h[N], ne[N], val[N], e[N], idx, sp[N]; //sp是否为普通边
void add(int a, int b, int c, int d)
{
e[idx] = b;
val[idx] = c;
ne[idx] = h[a];
sp[idx] = d;
h[a] = idx++;
}
struct Node
{
//顶点 距离 特殊边
int a, d, p;
bool operator < (const Node &a)const
{
return d > a.d;
}
};
bool vis[N][2];
int dis[N][2];
int tag[N];
void dij()
{
set<int> st;
//除起点以外的点放到set里面去
for (int i = 1; i <= n; i++)
{
if (i != s)st.insert(i);
vis[i][0] = vis[i][1] = 0;
dis[i][0] = dis[i][1] = INF;
}
dis[s][0] = 0;
priority_queue<Node> pq;
pq.push({s, 0, 0});
int cnt = 0;
while (pq.size())
{
auto t = pq.top();
int ty = t.p, ver = t.a;
pq.pop();
cnt++;
if (!ty) //普通边删除
{
st.erase(ver);
}
else
{
for (int i = h[ver]; ~i; i = ne[i])
{
int j = e[i];
tag[j] = cnt;
}
vector<int> tp;
for (auto cur : st)
{
if (tag[cur] != cnt) // 没有被遍历的非相邻的点
{
tp.push_back(cur);
dis[cur][0] = dis[ver][ty];
pq.push({cur, dis[cur][0], 0});
}
}
for (auto cur : tp)
{
st.erase(cur);
}
}
int y = 0;
if (ty) y -= k;
if (vis[ver][ty])continue;
vis[ver][ty] = 1;
for (int i = h[ver]; ~i; i = ne[i])
{
int j = e[i];
if (dis[j][sp[i]] > dis[ver][ty] + val[i] + y)
{
dis[j][sp[i]] = dis[ver][ty] + val[i] + y;
pq.push({j, dis[j][sp[i]], sp[i]});
}
}
}
}
void slove()
{
cin >> n >> m >> s >> k;
for (int i = 0; i <= n; i++)h[i] = -1, tag[i] = 0;
idx = 0;
for (int i = 1; i <= m; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
add(a, b, c, d);
}
dij();
for (int i = 1; i <= n; i++)
{
if (min(dis[i][0], dis[i][1]) == INF)cout << -1 << " ";
else cout << min(dis[i][0], dis[i][1]) << " ";
}
cout << '\n';
}
signed main()
{
IO
int _T = 1;
cin >> _T;
while (_T--)
{
slove();
}
return (0 - 0);
}
I Laser
平面几何,炮台能够消灭的方位\((x + k, y),(x, y + k),(x + k, y + k),(x + k, y − k)\)
如图(\(A\)点为武器所在位置)
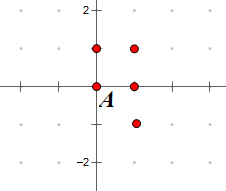
特殊情况:要是所有的点都处于水平/竖直/斜线上,是可以直接输出答案的。
普通情况:选一个点
点击查看代码
#include<iostream>
#define IO std::ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
using namespace std;
const int N = 1e6 + 10;
using ll = long long;
int x[N], y[N], a[N], b[N];
int n;
bool pd(int x, int y)
{
return x == y or x == 0 or y == 0 or x + y == 0;
}
bool chk(int xx, int yy)
{
for (int i = 0; i < n; i++)
{
if (!pd(xx - x[i], yy - y[i]))return 0;
}
return 1;
}
bool chk()
{
bool fa = 1;
for (int i = 1; i < n; i++)
{
if (x[i] == x[0])continue;
fa = 0;
if (chk(x[0], y[i]))return 1;
if (chk(x[0], y[i] + x[i] - x[0]))return 1;
if (chk(x[0], y[i] - x[i] + x[0]))return 1;
break;
}
return fa;
}
bool ans()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i] >> b[i];
x[i] = a[i];
y[i] = b[i];
}
if (chk())return 1;
for (int i = 0; i < n; i++)
{
x[i] = b[i];
y[i] = a[i];
}
if (chk())return 1;
for (int i = 0; i < n; i++)
{
x[i] = a[i] + b[i];
y[i] = a[i] - b[i];
}
if (chk())return 1;
for (int i = 0; i < n; i++)
{
x[i] = a[i] - b[i];
y[i] = a[i] + b[i];
}
if (chk())return 1;
return 0;
}
void slove()
{
if(ans())puts("YES");
else puts("NO");
}
int main()
{
IO
int t;
cin >> t;
while (t--)
{
slove();
}
return 0;
}
K Random
简单的概率题,直接能推出公式为\((n - m) / 2\)
但是不能就这样简单的去算,加减乘与模运算的顺序交换不会影响结果,但是除法不行。这个题目要求对一个大质数取模,原式里面有除法,我们就需要求取除数对于取模数的逆元,然后进行转化为乘法运算。
这样我们就需要先求出\(2\)对于\({10}^9+7\)的逆元\(x^{-1}\)(费马小定理转化一下,快速幂嗯算就完了)
这样计算公式为:
点击查看代码
#include<bits/stdc++.h>
int mod = 1e9+7;
int main()
{
int t = 1;
std::cin >> t;
int tem = 500000004;
while(t--)
{
int x,y;
std::cin >> x >> y;
std::cout << 1ll * (x-y) * tem % mod <<std::endl;
}
return 0;
}
L Alice and Bob
博弈论
如果有某个数\(n\)正好有\(2^{n}\)个,这样一直分下去是一定会出现\(0\)的,这样\(Alice\)是必赢的。
第\(i\)位所做的贡献为\(\frac{a[i]}{2^{i}}\),若是最后和大于\(0\),\(Alice\)就胜出
点击查看代码
#include<iostream>
const int N = 1e6 + 10;
using namespace std;
int a[N];
int n;
void slove()
{
cin >> n;
for(int i = 0;i <= n;i++)cin >> a[i];
for(int i = n;i > 0;i--)a[i-1] += a[i] / 2;
cout << a[0] << endl;
if(a[0])puts("Alice");
else puts("Bob");
}
int main()
{
int t;
cin >> t;
while(t--)slove();
return 0;
}
本文来自博客园,作者:肆月初陸丶,转载请注明原文链接:https://www.cnblogs.com/zarttic/p/16496065.html

 ybb
ybb

 浙公网安备 33010602011771号
浙公网安备 33010602011771号