fhqtreap笔记
引入
无旋转 \(treap\) ,又称分裂合并树,因为其操作由分裂合并实现,代码简单,好调,并且没有旋转操作,可能有时常数略大,但不影响其优秀。
原理
\(fhqtreap\) 是以 \(BST\) 二叉搜索树为基础实现的
不同于 \(BST\) 的是,加入数值时我们保存一个随机 \(key\) 值 ,并保证父亲的 \(key\) 值大于儿子的 \(key\) 值,使得树成为随机情况下的 \(BST\) ,树高降至 \(\log N\)
以下就是一颗 \(fhqtreap\)
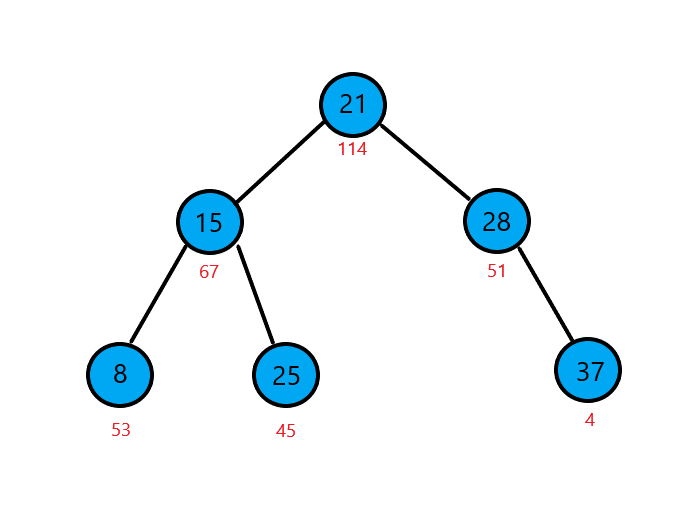
其中红色的值为 \(key\) , 黑色的值为数的值 \(val\)
假如我们查询 \(21\) 的排名,就把树分裂成 \(<=val\) 的一部分和 \(>val\) 的一部分
分裂后:
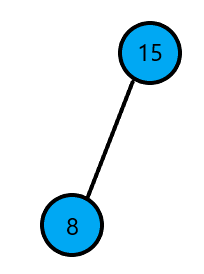
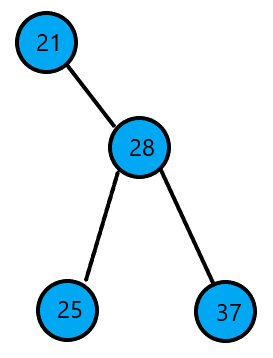
令第一部分的根节点为 \(l\)
则 \(rank(21)=\) \(l\) 的子树大小(包含 \(l\) ) \(+1=3\)
实现
基础操作
结构体:
struct node{
int l,r; //左右儿子
int val,key,s; //数值,随机值,size
};
更新
inline void pushup(int x){ t[x].s=t[t[x].l].s+t[t[x].r].s+1; }
新建节点
inline int newnode(int val){
++tot;
t[tot].l=t[tot].r=0;
t[tot].val=val;
t[tot].key=rnd();
t[tot].s=1;
return tot;
}
其中在代码前加上
std::mt19937 rnd(233);
避免普通 \(rand\) 全是 \(0\) 导致树被卡成一条链
Split 分裂
void split(int p,int val,int &l,int &r){
if(!p){
l=r=0;
return;
}
if(t[p].val<=val){
l=p;
split(t[p].r,val,t[p].r,r);
}else{
r=p;
split(t[p].l,val,l,t[p].l);
}
pushup(p);
}
其中 \(l\) 代表 \(<=val\) 树的根节点 , \(r\) 代表 \(>val\) 树的根节点
递归时如果 \(t[p].val <= val\) 就把 \(p\) 加到 \(l\) 的子树下 , 递归 \(t[p].r\)
否则就把 \(p\) 加到 \(r\) 的子树下,递归 \(t[p].l\)
merge 合并
分裂过后肯定要再合并回去
假设我们现在在合并 \(x\) ,\(y\)
因为 \(Split\) 过后 \(x\) 的所有节点的值都严格小于 \(y\) 的所有节点,所以我们只考虑两种情况
情况一: \(t[x].key>t[y].key\)
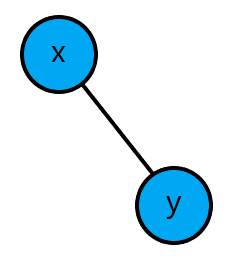
把 \(y\) 合并在 \(x\) 的右节点
情况二: \(t[x].key<=t[y].key\)
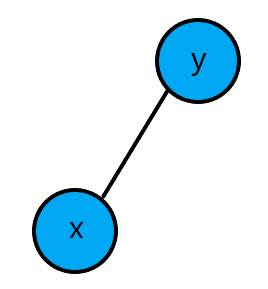
把 \(x\) 合并在 \(y\) 的左节点
代码:
int merge(int l,int r){
if(!l||!r) return l|r;
if(t[l].key>t[r].key){
t[l].r=merge(t[l].r,r);
pushup(l);
return l;
}else{
t[r].l=merge(l,t[r].l);
pushup(r);
return r;
}
}
insert 加入
设加入值 \(val\)
将树分裂成 \(<=val\) 和 \(>val\)
把 \(val\) 合并进去就行了
代码:
inline void insert(int val){
int dl,dr;
split(rt,val,dl,dr);
rt=merge(merge(dl,newnode(val)),dr);
return;
}
erase 删除
先保证删除的数一定存在
设删除值 \(val\)
把树分裂成三个部分 \(<val\) 和等于 \(=val\) 的以及 \(>val\) 三棵树
取出等于 \(val\) 的设根为 \(temp\)
由于可能有多个 \(val\) ,我们可以直接做 \(temp=merge(t[temp].l,t[temp].r)\)
最后再把 \(temp\) 合并回去
代码:
inline void erase(int val){
int dl,dr,temp;
split(rt,val,dl,dr);
split(dl,val-1,dl,temp);
temp=merge(t[temp].l,t[temp].r);
rt=merge(merge(dl,temp),dr);
return;
}
rank 排名
直接分裂出 \(<val\) 的树,设其根为 \(l\)
则 \(rank(val)=t[l].s+1\)
代码:
inline int rank(int val){
int dl,dr;
split(rt,val-1,dl,dr);
int rnk=t[dl].s+1;
rt=merge(dl,dr);
return rnk;
}
rank_find 求排名为k的数
与 \(BST\) 的查找相同
若搜索的节点为 \(p\) ,如果 \(t[t[p].l].s+1=k\) ,返回 \(t[p].val\)
否则如果 \(t[t[p].l].s>=k\) ,递归查找 \(p=t[p].l\)
否则 \(k-=(t[t[p].l].s+1)\) , 递归查找 \(p=t[p].r\)
代码:
inline int rank_find(int rnk){
int p=rt;
while(true){
if(t[t[p].l].s+1==rnk) break;
else if(t[t[p].l].s>=rnk) p=t[p].l;
else rnk-=t[t[p].l].s+1,p=t[p].r;
}
return t[p].val;
}
pre 最大的数且严格小于val(前驱)
先分裂出 \(<val\) 的树,设根为 \(l\)
因为要求最大,可以一直查找当前右节点直到叶子结点
代码:
inline int pre(int val){
int dl,dr;
split(rt,val-1,dl,dr);
int p=dl;
while(t[p].r) p=t[p].r;
rt=merge(dl,dr);
return t[p].val;
}
suf 最小的数且严格大于val (后继)
同理,分裂出 \(>val\) 的树再递归右节点即可
代码:
inline int suf(int val){
int dl,dr;
split(rt,val,dl,dr);
int p=dr;
while(t[p].l) p=t[p].l;
rt=merge(dl,dr);
return t[p].val;
}
实现普通平衡树 P3369
#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define drep(i,x,y) for(int i=x;i>=y;i--)
#define ll long long
#define pb push_back
#define lb long double
using namespace std;
std::mt19937 rnd(233);
template<int T> struct fhq_treap{
struct node{
int val,key,l,r,s;
}t[T+5];
int tot,rt,size;
fhq_treap(){ tot=0; rt=0; size=0; }
int newnode(int val){
tot++;
t[tot].s=1;
t[tot].l=t[tot].r=0;
t[tot].val=val;
t[tot].key=rnd();
return tot;
}
inline void pushup(int u){ t[u].s=t[t[u].l].s+t[t[u].r].s+1; }
void split(int p,int val,int &l,int &r){
if(!p) {
l=r=0;
return;
}
if(t[p].val<=val){
l=p;
split(t[p].r,val,t[p].r,r);
}else{
r=p;
split(t[p].l,val,l,t[p].l);
}
pushup(p);
}
int merge(int l,int r){
if(!l||!r) return l|r;
if(t[l].key>t[r].key){
t[l].r=merge(t[l].r,r);
pushup(l);
return l;
}else{
t[r].l=merge(l,t[r].l);
pushup(r);
return r;
}
}
inline void insert(int val){
int dl=0,dr=0; size++;
split(rt,val,dl,dr);
rt=merge(merge(dl,newnode(val)),dr);
}
inline void erase(int val){
int dl=0,dr=0,temp=0; size--;
split(rt,val,dl,dr);
split(dl,val-1,dl,temp);
temp=merge(t[temp].l,t[temp].r);
rt=merge(merge(dl,temp),dr);
}
inline int rank(int val){
int dl=0,dr=0;
split(rt,val-1,dl,dr);
int rnk=t[dl].s+1;
rt=merge(dl,dr);
return rnk;
}
inline int rank_find(int rnk){
return get_rank(rt,rnk);
}
int get_rank(int p,int rnk){
if(t[t[p].l].s+1==rnk) return t[p].val;
if(rnk<t[t[p].l].s+1) return get_rank(t[p].l,rnk);
else return get_rank(t[p].r,rnk-t[t[p].l].s-1);
}
inline int pre(int val){
int dl,dr;
split(rt,val-1,dl,dr);
int p=dl;
while(t[p].r) p=t[p].r;
rt=merge(dl,dr);
return t[p].val;
}
inline int suf(int val){
int dl,dr;
split(rt,val,dl,dr);
int p=dr;
while(t[p].l) p=t[p].l;
rt=merge(dl,dr);
return t[p].val;
}
};
fhq_treap<100010> t;
int q;
int main(){
sf("%d",&q);
while(q--){
int opt,x;
sf("%d%d",&opt,&x);
if(opt==1) t.insert(x);
else if(opt==2) t.erase(x);
else if(opt==3) printf("%d\n",t.rank(x));
else if(opt==4) printf("%d\n",t.rank_find(x));
else if(opt==5) printf("%d\n",t.pre(x));
else printf("%d\n",t.suf(x));
}
return 0;
}
加强版代码也差不多,就不给了
实测加强版最慢的点跑了 \(906ms\) ,离 \(3.0s\) 还是挺远的
P1486 [NOI2004] 郁闷的出纳员
很明显的板子
实现呢我写的是每个点打一个 \(tag\) (其实可以不用)
询问到他的时候像线段树一样下传
对于离开的打工人我们只需要在扣工资的时候把值小于 \(min\) 的一部分 分裂出来
只留大于等于的即可
代码 :
#include<bits/stdc++.h>
#define ll long long
#define sf scanf
#define pf printf
#define pb push_back
#define cmax(x,y) x=max(x,y);
#define cmin(x,y) x=min(x,y);
#define ull unsigned long long
#define drep(i,x,y) for(int i=x;i>=y;i--)
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define IOS ios::sync_with_stdio(false)
using namespace std;
inline ll in(){ ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') (ch=='-'?f=-1:1),ch=getchar(); while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar(); return x*f; }
std::mt19937 rnd(233);
ll mi;
template<int T> struct fhq{
struct node{
int l,r,s,key;
ll val,tag;
}t[T+5];
int tot,rt,cnt;
fhq(){
tot=rt=0;
cnt=0;
}
inline int newnode(int val){
tot++;
t[tot].s=1;
t[tot].l=t[tot].r=0;
t[tot].val=val;
t[tot].key=rnd();
t[tot].tag=0;
return tot;
}
inline int pushup(int x){
t[x].s=t[t[x].l].s+t[t[x].r].s+1;
}
inline void down(int x){
if(t[x].tag!=0){
t[t[x].l].val+=t[x].tag;
t[t[x].r].val+=t[x].tag;
t[t[x].l].tag+=t[x].tag;
t[t[x].r].tag+=t[x].tag;
t[x].tag=0;
return;
}
}
void split(int p,ll val,int &l,int &r){
if(!p) {
l=r=0;
return;
}
down(p);
if(t[p].val<=val){
l=p;
split(t[p].r,val,t[p].r,r);
}else{
r=p;
split(t[p].l,val,l,t[p].l);
}
pushup(p);
}
int merge(int l,int r){
if(!l||!r) return l|r;
if(t[l].key>t[r].key){
down(l);
t[l].r=merge(t[l].r,r);
pushup(l);
return l;
}else{
down(r);
t[r].l=merge(l,t[r].l);
pushup(r);
return r;
}
}
inline void insert(ll val){
if(val<mi) return;
int dl,dr;
split(rt,val,dl,dr);
rt=merge(merge(dl,newnode(val)),dr);
}
inline int rank_find(int rnk){
if(rnk>t[rt].s) return -1;
rnk=t[rt].s-rnk+1;
int p=rt,cnt=0;
while(1){
down(p);
if(t[t[p].l].s+1==rnk) return t[p].val;
else if(t[t[p].l].s+1<rnk) rnk-=t[t[p].l].s+1,p=t[p].r;
else p=t[p].l;
}
}
inline void add(ll val){
t[rt].tag+=val;
t[rt].val+=val;
if(val<0){
int dl,dr;
split(rt,mi-1,dl,dr);
cnt+=t[dl].s;
rt=dr;
}
}
};
fhq<300020> t;
int n;
int main(){
n=in(); mi=in();
while(n--){
char op[9];
ll v;
sf("%s",op+1);
sf("%lld",&v);
if(op[1]=='I'){
t.insert(v);
}else{
if(op[1]=='F'){
pf("%d\n",t.rank_find(v));
}else{
if(op[1]=='S') v=-v;
t.add(v);
}
}
}
pf("%d\n",t.cnt);
return 0;
}
P3224 [HNOI2012] 永无乡
简化题意:联通块合并,联通块第 \(k\) 大
首先考虑由并查集维护联通块
有个坑点,就是合并两个联通块的时候注意不能直接 \(merge\) ,因为 \(fhqtreap\) 的 \(merge\) 要有 \(l\) 中所有节点都小于 \(r\) 的节点
所以我们暴力遍历另一个联通块中的数并 \(insert\) 到联通块的树里
查询就 \(rankfind\) 正常做就行了
但是普通暴力做着是 \(n ^ 2 \log n\) 的,考虑启发式合并优化,最后总复杂度
\(n \log^2 n\) 常数比较小,开 \(O2\) 最慢才 \(180ms\)
代码:
#include<bits/stdc++.h>
#define ll long long
#define rep(i,x,y) for(int i=(x);i<=(y);i++)
#define drep(i,x,y) for(int i=(x);i>=(y);i--)
#define sf scanf
#define pf printf
#define pb push_back
#define pii pair<int,int>
#define i128 __int128
#define pt putchar
using namespace std;
inline ll in(){ ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') (ch=='-'?f=-1:1),ch=getchar(); while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar(); return x*f; }
std::mt19937 rnd(233);
template<int T> struct fhq{
struct node{
int l,r,s,val,key;
}t[T+5];
int f[T+5],rt[T+5],id[T+5];
int tot;
fhq(){
tot=0;
rep(i,1,T) rt[i]=f[i]=i;
}
inline int newnode(int val){
t[++tot]={0,0,1,val,rnd()};
return tot;
}
inline void pushup(int x){
t[x].s=t[t[x].l].s+t[t[x].r].s+1;
}
void split(int p,int val,int &l,int &r){
if(!p){
l=r=0;
return;
}
if(t[p].val<=val){
l=p;
split(t[p].r,val,t[p].r,r);
}else{
r=p;
split(t[p].l,val,l,t[p].l);
}
pushup(p);
}
int merge(int l,int r){
if(!l||!r) return l|r;
if(t[l].key>t[r].key){
t[l].r=merge(t[l].r,r);
pushup(l);
return l;
}
t[r].l=merge(l,t[r].l);
pushup(r);
return r;
}
int get(int x){
if(f[x]==x) return x;
return f[x]=get(f[x]);
}
inline void insert(int x,int y){
int dl,dr;
split(rt[x],t[y].val-1,dl,dr);
rt[x]=merge(merge(dl,y),dr);
}
void dfs(int u,int fa){
if(!u) return;
dfs(t[u].l,fa);
int r=t[u].r;
t[u].l=t[u].r=0;
t[u].s=1;
insert(fa,u);
dfs(r,fa);
}
inline void vmerge(int x,int y){
int fx=get(x),fy=get(y);
if(fx==fy) return;
if(t[rt[fx]].s<t[rt[fy]].s) swap(fx,fy);
dfs(fy,fx);
f[fy]=fx;
}
inline int ask(int x,int k){
int fx=rt[get(x)],p=fx;
if(t[fx].s<k) return -1;
while(1){
if(t[t[p].l].s+1==k) return id[t[p].val];
if(t[t[p].l].s+1>k) p=t[p].l;
else k-=(t[t[p].l].s+1),p=t[p].r;
}
}
};
fhq<300030> t;
int n,m;
int main(){
sf("%d%d",&n,&m);
rep(i,1,n){
int x=in();
t.id[x]=i;
t.newnode(x);
}
while(m--){
int u,v;
u=in(); v=in();
t.vmerge(u,v);
}
m=in();
while(m--){
char op[5];
int x,y;
sf("%s",op+1);
x=in();y=in();
if(op[1]=='Q') pf("%d\n",t.ask(x,y));
else t.vmerge(x,y);
}
return 0;
}
代码有点丑,因为一开始题读错了,求的是第 \(k\) 大的编号而不是值
实现文艺平衡树
平衡树实现区间操作时存的 \(val\) 改成下标
每次翻转分裂出 \(l\) ~ \(r\) 区间并打上翻转标记,在 \(merge\) 时下传即可
具体看实现:
#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(i,x,y) for(int i=x;i<=y;i++)
#define drep(i,x,y) for(int i=x;i>=y;i--)
#define ll long long
#define pb push_back
#define lb long double
using namespace std;
inline ll in(){ ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') (ch=='-'?f=-1:1),ch=getchar(); while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar(); return x*f; }
std::mt19937 rnd(233);
template<int T> struct fhq{
struct node{
int l,r,s,val,key;
int rev;
}t[T*2+5];
int tot=0,rt=0;
inline int newnode(int val){
t[++tot]={0,0,1,val,rnd(),0};
return tot;
}
inline void pushup(int x){
t[x].s=t[t[x].l].s+t[t[x].r].s+1;
}
inline void down(int x){
if(t[x].rev){
swap(t[x].l,t[x].r);
t[t[x].l].rev^=1;
t[t[x].r].rev^=1;
t[x].rev=0;
return;
}
}
void split(int p,int val,int &l,int &r){
if(!p){
l=r=0;
return;
}
down(p);
if(t[t[p].l].s+1<=val){
l=p;
split(t[p].r,val-t[t[p].l].s-1,t[p].r,r);
}
else{
r=p;
split(t[p].l,val,l,t[p].l);
}
pushup(p);
}
int merge(int l,int r){
if(!l||!r) return l|r;
if(t[l].key<t[r].key){
down(l);
t[l].r=merge(t[l].r,r);
pushup(l);
return l;
}
down(r);
t[r].l=merge(l,t[r].l);
pushup(r);
return r;
}
inline void insert(int val){
int dl,dr;
split(rt,val-1,dl,dr);
rt=merge(merge(dl,newnode(val)),dr);
}
inline void reverse(int l,int r){
int dl,temp,dr;
split(rt,l-1,dl,dr);
split(dr,r-l+1,temp,dr);
t[temp].rev^=1;
rt=merge(merge(dl,temp),dr);
}
inline void dfs(int u){
if(!u) return;
down(u);
dfs(t[u].l);
pf("%d ",t[u].val);
dfs(t[u].r);
}
};
fhq<100005> t;
int n,m;
int main(){
n=in(); m=in();
rep(i,1,n) t.insert(i);
rep(i,1,m) {
int l=in(),r=in();
t.reverse(l,r);
}
t.dfs(t.rt); pf("\n");
return 0;
}
闲话
考试的时候双 \(split\) 的 \(fhq\) 花了 \(2h\) 没调出来,等我调出来了继续更双 \(split\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号