云台姿态解算

欧拉角的旋转矩阵如下

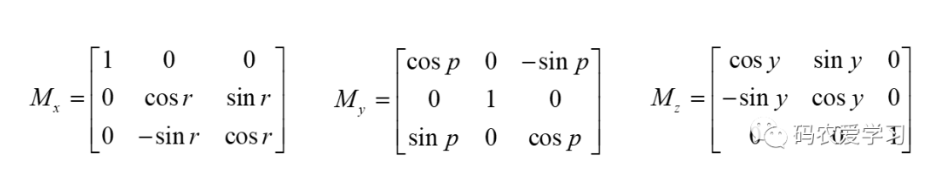
加速度计在旋转时产生的分量本质上是大地坐标系下$ (0,0,g)
$在机器人坐标系下的新坐标，也就是

$ \left[
\begin{matrix}
a_x\a_y\a_z
\end{matrix}
\right]

M_xM_yM_z
\left[
\begin{matrix}
0\0\g
\end{matrix}
\right] $

计算过程省略，结果如下

$ roll=\arctan{\frac{a_y}{a_x}}

$

$ pitch=-arctan{\frac{a_x}{\sqrt{a_y^2+a_z2}}} $

yaw角视为0

欧拉角和四元数的转换如下

$ q_{0}=\cos \dfrac{\phi }{2}\cos \dfrac{\theta}{2}\cos \dfrac{\psi}{2}+\sin \dfrac{\phi }{2}\sin \dfrac{\theta}{2}\sin \dfrac{\psi}{2}\ \ \
q_{1}=\sin \dfrac{\phi }{2}\cos \dfrac{\theta}{2}\cos \dfrac{\psi}{2}-\cos \dfrac{\phi }{2}\sin \dfrac{\theta}{2}\sin \dfrac{\psi}{2}\ \ \
q_{2}=\cos \dfrac{\phi }{2}\sin \dfrac{\theta}{2}\cos \dfrac{\psi}{2}+\sin \dfrac{\phi }{2}\cos \dfrac{\theta}{2}\sin \dfrac{\psi}{2}\ \ \
q_{3}=\cos \dfrac{\phi }{2}\cos \dfrac{\theta}{2}\sin \dfrac{\psi}{2}+\sin \dfrac{\phi }{2}\sin \dfrac{\theta}{2}\cos\dfrac{\psi}{2} $

于是就得到了在云台姿态解算线程中，欧拉角初始化函数Atti_FirstUpdate

void Atti_FirstUpdate(AHRS_Accl_t *Accl)
{
    AHRS_Eulr_t first_euler = {0};
    float ax, ay, az;

    ax = Accl->x;
    ay = Accl->y;
    az = Accl->z;

    // 初始姿态(欧拉角)
    first_euler.pit = -atan2f(ax, sqrtf(az * az + ay * ay));
    first_euler.rol = atan2f(ay, az);
    first_euler.yaw = 0.0f;

    // 欧拉角转四元数
    AHRS_Euler2Quarternion(&first_euler, &HERO_AHRS);
}