数论1——质数与约数

质数：

1、判断质数

试除法：从2开始循环，到判断数 X 的sqrt（X）为止即可，若存在约数，则一定<=sqrt(X)，不然则本身为质数。（由于约数本身的成对出现的，若小于等于没有，则大于也不会存在

时间复杂度为O(sqrt(x)）

bool is_prime(int num){
    if(num<2) return false;
    for(int i=2;i<=num/i;i++){
        if(num%i==0) return false;
    }
    return true;
}

2、分解质因数

总体思路和上面的试除法结合，在找到某数的质因数后，利用while循环把相关质因数除尽，然后找下一个质因数

时间复杂度为O(sqrt(x)*log(sqrt(x)))

（下面代码中，v是vector）；

for(int i=2;i<=sqrt(num);i++){
        if(num%i==0){
            v.push_back(i);
            while(num%i==0){
                num/=i;
            }
        }
    }

3、筛质数

普通筛

先把所有待找的数定为false，然后找到一个数，不管该数是不是质数都把该数的倍数设置为true（这里就会导致很多的重复），在最后，留下来的false就是质数

时间复杂度为O(nlog(n))

void primes_table(){ 

    memset(st,0,sizeof(st));

    for(int i=2;i<=n;i++){

        if(!st[i]) primes[cnt++]=i;//把质数放到相应的数组中去

        for(int j=i;j<=n;j+=i){
            st[j]=true;
        }
    }

    return;
}

埃氏筛

在普通筛的基础上，只有找到质数的时候，才会去筛选合数，降低了重复率，但还是会筛重复的合数。

时间复杂度为O(nloglog(n))

void primes_table(){ 

    memset(st,0,sizeof(st));

    for(int i=2;i<=n;i++){

        if(!st[i]) {
        primes[cnt++]=i;//把质数放到相应的数组中去

            for(int j=i;j<=n;j+=i){
                st[j]=true;
            }
        }
    }

    return;
}    

线性筛：

在筛选的过程中，用每个数的最小质因子去筛选各个合数

时间复杂度为O(n)

void primes_table(){ 

    memset(st,0,sizeof(st));
    int cnt=0;

    for(int i=2;i<=n;i++){

        if(!st[i]) {
        primes[cnt++]=i;//把质数放到相应的数组中去
        }
        for(int j=0;prime[j]*i<=n;j+=i){
              st[prime[j]*i]=true;
              if(i%prime[j]==0) break;
         }
    }

    return;
} 

约数：

求约数

   约数的求解和试除法相对应，由于约数的出现总是成对出现，当出现一个约数小于等于sqrt（x）时，总存在另一个约数大于等于sqrt（x），所有在寻找约数的过程中，只需要找从1~

sqrt（x）这段范围即可

for(int i=1;i<=sqrt(num);i++){
        if(num%i==0) {
            v.push_back(i);
            if(i!=sqrt(num)) v.push_back(num/i);
        }
    }

约数之和：

 

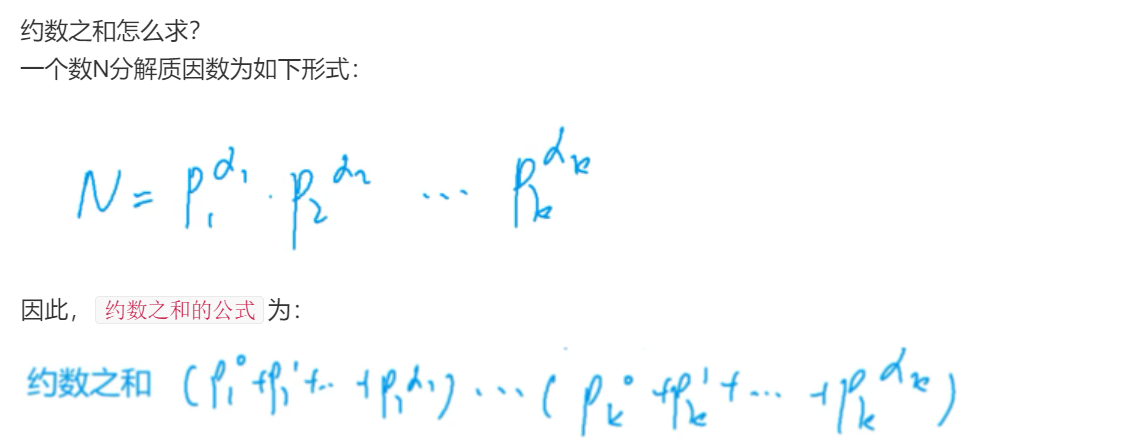
 其中p1,p2为质数，a1，a2为次数，可以调用之前分解质因数的方法得到该数分解质因数后的结果，用map存储

然后运用约数之和的公式计算（在计算之和时，用递归一次一次算，不然容易爆）

void apart(long long num){
    for(int i=2;i<=sqrt(num);i++){
        while(num%i==0){
            m[i]++;
            num/=i;
        }
    }
    if(num!=1) m[num]++;
    return ;
}
long long sum(long long a,long long b){
    long long ans=1;
   // pow(a*1.0,b*1.0+1)-1)/(a-1);这个会爆数，不能用
    while(b--){
        ans=(ans*a+1)%M;
    }
   // cout<<ans<<endl<<endl;
    return ans;
}

 

约数个数

 

 

最大约数——辗转相除法，gcd算法（最大公因子）

long long gcd(long long a,long long b) {
    cout<<a<<" "<<b<<endl;
    if(a%b==0) return b;
    else return gcd(b,a%b);
}

 

欧拉函数