解题报告(离散化处理前缀和类问题)
在谈到离散化之前,可以从简单的前缀和问题上入手,来理解离散化处理问题的精妙
Acwing 795 前缀和

(该题限时2s)
对于小范围的前缀和,可以先开n大小的数组,存储整数序列,其中再开另外一个n大小的数组s,用来存储到达每一个下标前的前缀和。即s [i]=s [i-1]+a [i]; 此后在询问区间内的和的时候,直接s [r]- s [l-1] 即为区间和;(这里是l-1是因为下标为 l 的话,就少减去了s [l]); 对于本题来说,l,r的数据范围是到 [1,1e5],数组下标直接用来表示l,r的话,也够用。但是,当l,r的范围扩大到1e9的时候,数组开不了那么大,此时不能单单用数组下标来表示了。
如题:
Acwing 802 区间和

如果该题我们用上一题的思路去解,首先我们就需要开一个2e9大小的数组,此时需要大概有4个G的内存空间才行,内存受限。而我们观察题目,总共对于点的个数也就1e5个,对于没有用到的点的初始值也就是为0,对于前缀和来说,是没有任何影响的。所以,相当于开2e9大小的数组有相当一部分都是浪费了的,所以我们不能一个点一个位置都给分配。由于我们用到的点,就是一个点一个点的零散的点,所以也就是利用离散化的方式,将这些点,映射到一个数组中去,这就是离散化的处理方式。
离散化过程:
若现在有1,2,1e7,1e9。四个点的数存在某个数组中,并且各个点对应各自的值
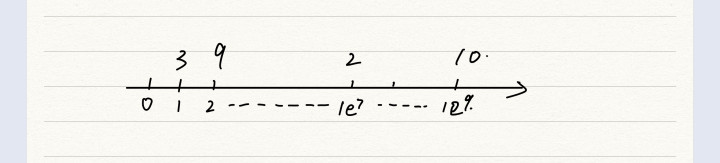
接下来将该点整理到一个数组中,从大到小。也就是将该数组的下标变成了离散数的下标,离散数变成了该数组的各个元素

实际上,就是将其做下图的对应方式。
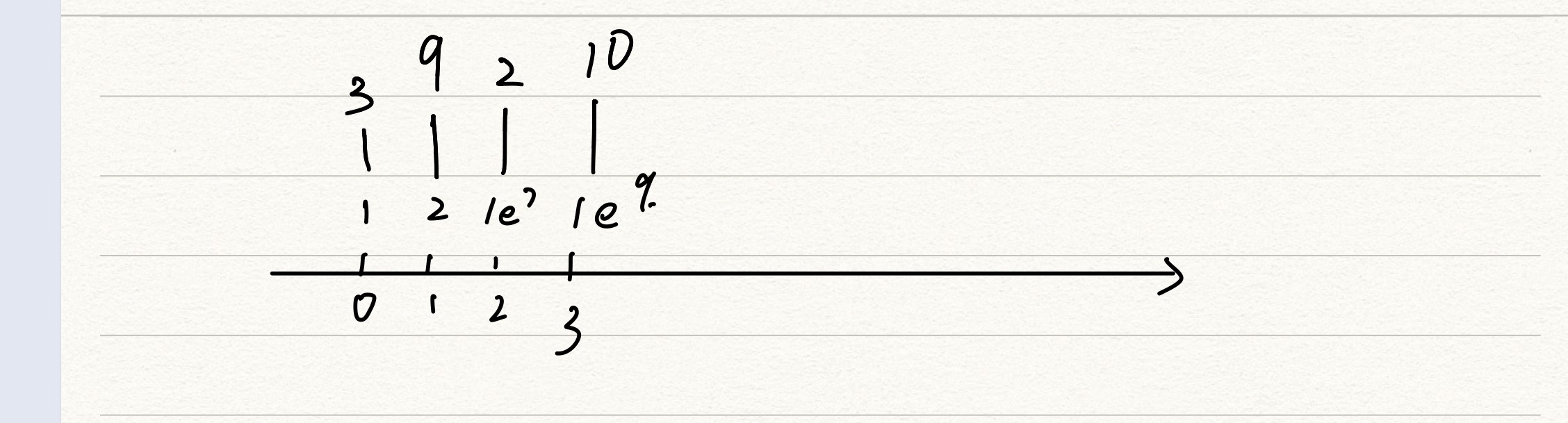
当元素有重复的时候,我们需要去除重复的元素。
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());
去重的理由在于:
当存在两个相同的元素的时候,他们映射的数是不同的,而通过二分查找的,找到的都是前一个元素的映射的数,此时去除可以减少映射数组的内存大小,提高二分的效率
接下来,当我们需要用到这些点的时候,就可以从这个数组中去找。
如何找,如果从头到尾遍历就慢了,还是O(n)的时间复杂度,这里采用二分的算法,可以从O(n)到O(logn);
int find(int x)//找相应的下标 { int l=0,r=alls.size(); while(l<r) { int mid=(l+r)/2; if(alls[mid]>x) r=mid; else if(alls[mid]<x) l=mid; else return mid+1; //cout<<l<<r<<endl; } return r+1;//这里返回的是r+1是因为数组是从0开始,但是接下来计算前缀和的话,最好是从1开始,比较好计算 }
例题:
Acwing 802 区间和(即上题)

对于本题来说,各个点的数值其实是零散开来,我们首先需要一个数组来记录所有的区间端点数值,包括x,l, r。可记作数组a
对于特殊的点,即端点有自己的value值的点,我们需要用结构体来将其包装,因为一个点对应一个值,放入对应的数组中,记作数组b。
对于题目要求的区间值,我们也需要一个数组来储存,在输出答案的时候。(因为前期为了把区间端点值放到数组a中,已经读过一遍了,后期要输出,还要拿出来)记作数组c。
我们要用作计算前缀和的数组记作前缀数组a1,记录需要我们计算的各个点的值,记总和为前缀和数组s1,用a1中的数值将其转化为前缀和的形式,再输出
此时的时间复杂度是<=O((n+m)log(n+m));//具体看有无去重
#include<iostream> #include<vector> #include<algorithm> using namespace std; const int M=1e6+5; typedef pair<int,int> PI; vector<int>alls;//alls就是用来映射的映射数组,配合find函数找点的对应的映射下标 vector<PI>add,query;//add是存储对点的操作数,query是存储区间值 int a[M],s[M]; int find(int x)//找相应的下标,其实就是映射函数,找到的是大数映射的下标 { int l=0,r=alls.size(); while(l<r) { int mid=(l+r)/2; if(alls[mid]>x) r=mid; else if(alls[mid]<x) l=mid; else return mid+1; //cout<<l<<r<<endl; } return r+1; } int main() { int n,m; cin>>n>>m; for(int i=0;i<n;i++)//读入对点操作的数 { int x,c; cin>>x>>c; add.push_back({x,c}); alls.push_back(x); } for(int i=0;i<m;i++) { int l,r; cin>>l>>r; query.push_back({l,r}); alls.push_back(l); alls.push_back(r); } //去重 sort(alls.begin(),alls.end()); alls.erase(unique(alls.begin(),alls.end()),alls.end()); for(auto item: add) { int i=find(item.first);//找该数的映射下标 a[i]+=item.second; } for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];//计算前缀和 for(auto item: query) { int l=find(item.first),r=find(item.second); cout<<s[r]-s[l-1]<<endl; } return 0; }
该题是模板题,接下来是题目的小变式
Acwing 1952金发姑娘和N头牛

对于本题来说,用暴力的思想去看,就是对三段区间内加上x,y,z。(给出A,B值,在区间[1,A-1]上加上x,在区间[A,B]上加上y,在区间[B+1,1e9]上加上z),本质上还是需要对一段区间做操作,为了降低复杂度,可以采用差分的做法。即对每一个操作
是a[1]+=x,a[A]-=x,a[A]+=y,a[B+1]-=y,a[B+1]+=z。最后计算前缀和最大的值,就是题目所求的答案。而由于每个点的范围大,而点的数量小,需要用离散化来处理各个端点
#include<iostream> #include<algorithm> #include<cstring> #include<vector> using namespace std; const int M=2e6+5; int a[M],s[M]; typedef pair<int,int> PII; vector<int>all;//用来映射的数组 vector<PII>add,que; int find(int x)//映射函数 { int l=0,r=all.size(); while(l<r) { int mid=(l+r)/2; if(all[mid]>=x) r=mid; else l=mid+1; } return r+1; } int main() { memset(a,0,sizeof(a)); int n,x,y,z; cin>>n>>x>>y>>z; for(int i=0;i<n;i++) { int l,r; cin>>l>>r; all.push_back(l); all.push_back(r); que.push_back({l,r}); } int ans=0; sort(all.begin(),all.end()); //去重 all.erase(unique(all.begin(),all.end()),all.end()); for(auto item : que) { int l=find(item.first),r=find(item.second); a[1]+=x; a[l]-=x; a[l]+=y; a[r+1]-=y; a[r+1]+=z; //这里也可以整合一下,写成a[1]+=x;a[l]+=y-x;a[r+1]+=z-y; } for(int i=1;i<=all.size();i++) { a[i]+=a[i-1];//计算前缀和 ans=max(ans,a[i]); } cout<<ans; }
Acwing 1987 粉刷栅栏

对于本题来说,也可以转化为对区间做一次操作,即当奶牛走过[L,R]的区间的时候,在[L,R]上加上1。当一个区间内的值是大于二的时候,说明就是不止走了两遍
有一些问题需要转化:
对于[L,R]来说,当向右走的时候,L就起始点,R就是L+向左走的步长
当向左的时候,L就是上一次向右走的位置D-向右走的步长,R就是D,上一次的起始位置
而判断一个区间内的值大于二,可以用前缀和来判断,当某点的前缀和大于2的时候,说明这个点,奶牛已经经过了两次了,那么这个点到下一个点之间的距离,奶牛肯定要走。若是奶牛走的路程不止下一个点,那么在前缀和计算到下一个点的时候,下一个点的初始值应该是1。由于也是区间操作问题,最好用差分算法来降低时间复杂度,而在本题中,注意差分的后一个点是a[R]--;
由下图可知,对于右端点来说,是不算走过的路,因为计算下一段前缀和的时候,还是从右端点开始,会重复计算。
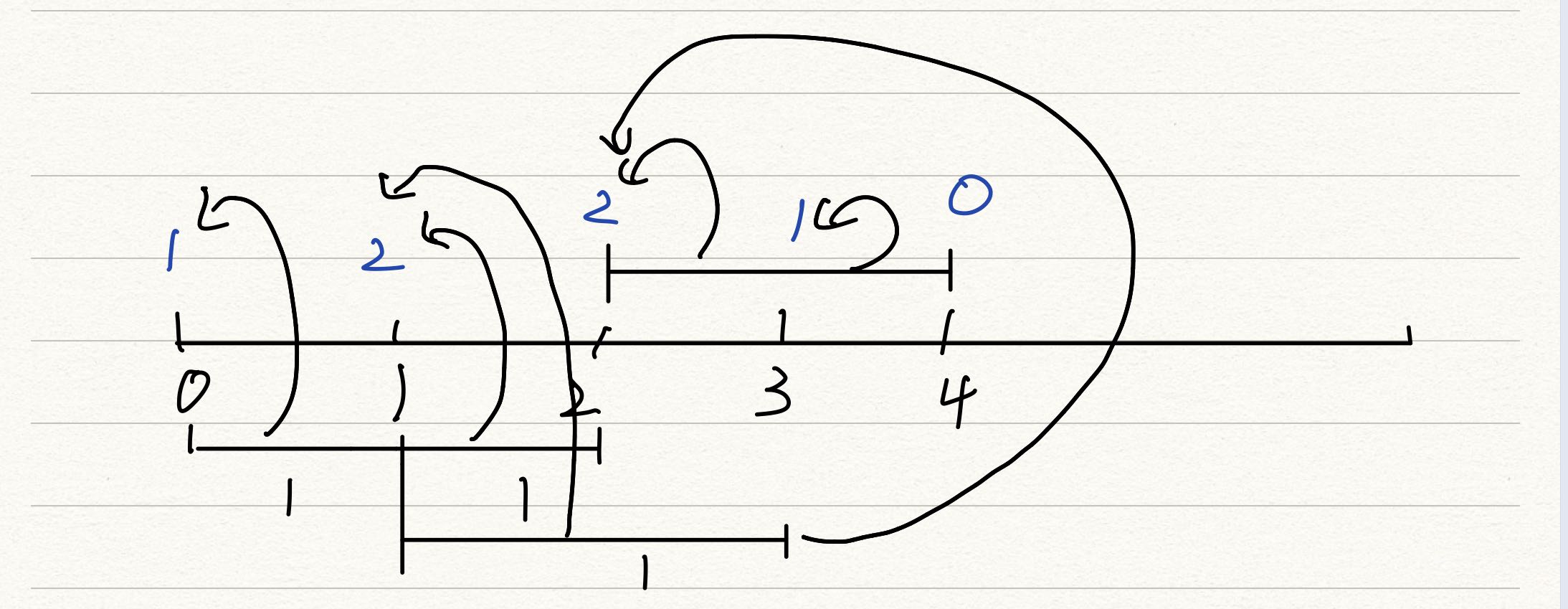
(箭头表示:当前点的前缀和的值是从哪几段来的)
而由于贝茜的行走距离的范围是[1,2e9],数值过大,想要直接用下标来表示走做的坐标的话,数组开的内存太大了,而且点是零散的,各个点的默认值为0,对前缀和也没有影响,所以也需要用离散化来储存各个点。
#include<iostream> #include<cstring> #include<algorithm> #include<vector> using namespace std; const int M=1e6+5; typedef pair<int,int>PII; vector<int>all; vector<PII>query; int a[M],s[M]; int find(int x) { int l=0,r=all.size(); while(l<r) { int mid=(l+r)/2; if(all[mid]>=x) r=mid; else l=mid+1; } return r+1; } int main() { memset(s,0,sizeof(s)); int n,sum=0;//查看总共走过了多少路径 cin>>n; int l=0; for(int i=0;i<n;i++) { int length,r; char c; cin>>length>>c; if(c=='L') r=l-length; else r=l+length; all.push_back(l); all.push_back(r); if(c=='R') query.push_back({l,r}); else query.push_back({r,l}); //cout<<l<<" "<<r<<endl; l=r;//是下一个点从上一个点的目的地开始 } sort(all.begin(),all.end()); all.erase(unique(all.begin(),all.end()),all.end()); for(auto item: query) { int li=find(item.first),ri=find(item.second);//找到映射的下标 // cout<<li<<" "<<ri<<endl; //标记走过的路段,用差分 a[li]++; a[ri]--;//这里不是a[r+1] } for(int i=1;i<=all.size();i++) { s[i]=s[i-1]+a[i];//计算前缀和表示走过的路段总路径 //cout<<s[i]<<" "<<a[i]<<endl; if(s[i]>=2) sum+=all[i]-all[i-1];//这里注意,由于传回来的是r+1,all数组的下标和前缀和数组想要表达的下标的差一 } cout<<sum; }
To sum up:
一般离散化是为了处理点的数量是不多,但是点的值较大,数组太大开不了的问题,可以将这些点映射到一个数组中去,用二分法来代替数组直接的用指针访问下标。
核心的代码就是去重,以及利用二分去查找下标



 浙公网安备 33010602011771号
浙公网安备 33010602011771号