games101学习：lecture 6 : Rasterization 2(antialiasing and Z-buffering)

今天要处理的东西是这两样：

1. antialising：反走样，为了减少锯齿出现所采取的方法。
2. Z-buffering：深度缓冲

今天学的难得多了！

上节课提到了在MVP（model view projection）之后还有适口的变换，还要将(-1,1)的三次方映射到屏幕上。

光栅化的定义：把东西画到屏幕上去。

计算机图形学一切看上去不太对的问题，错误等等都可以叫做Sampling Artifacts。
1.锯齿。
2.摩尔纹。（为了减少工作量忽略了显示偶数行和列）
3.轮子倒转效应？
4.还有更多……

背后的现象：信号变化太快了，但是采样速度更不上。就会导致走样。

一般如何做反走样(先说结果，再说原因)：再采样之前先做一个Blurring,或者说滤波。

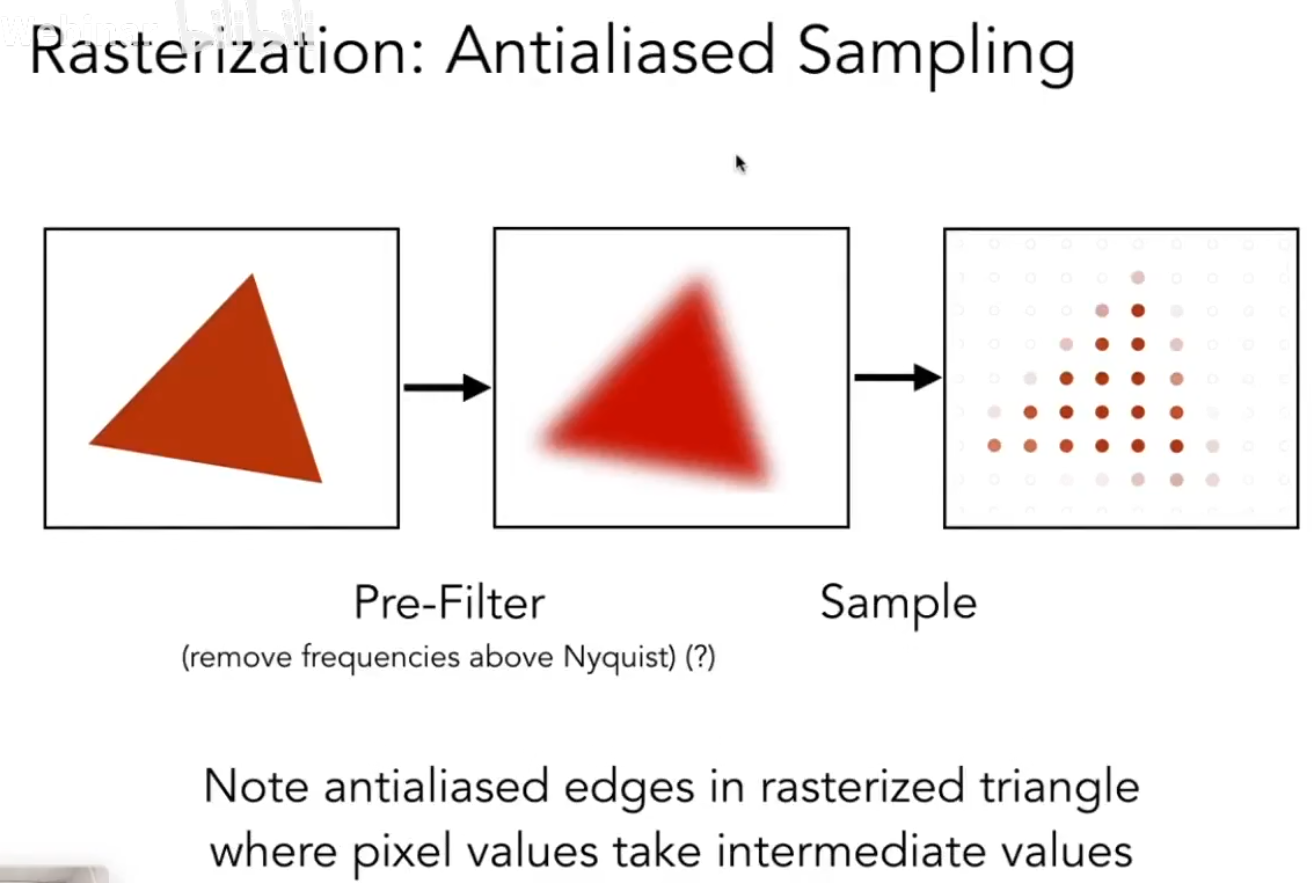
可以这样采样模糊的三角形，对原始的函数和信号进行滤波就可以解决锯齿这个问题。

先做滤波在做采样。

问：我们一般是先对信号作模糊，然后再进行采样。那我们能不能反过来，先进行采样，然后再对信号作模糊呢？
答：不行

会有这样。

为什么先滤波再采样可以做到反走样。

** Frequency Domain(频域)**

Fourier Transfrom（傅立叶级数展开）： 任何一个周期函数都可以写为一系列正弦和余弦函数的线性组合以及一个常数项，但是需要无穷项。

傅立叶级数展开适合傅立叶变换紧密相连的。

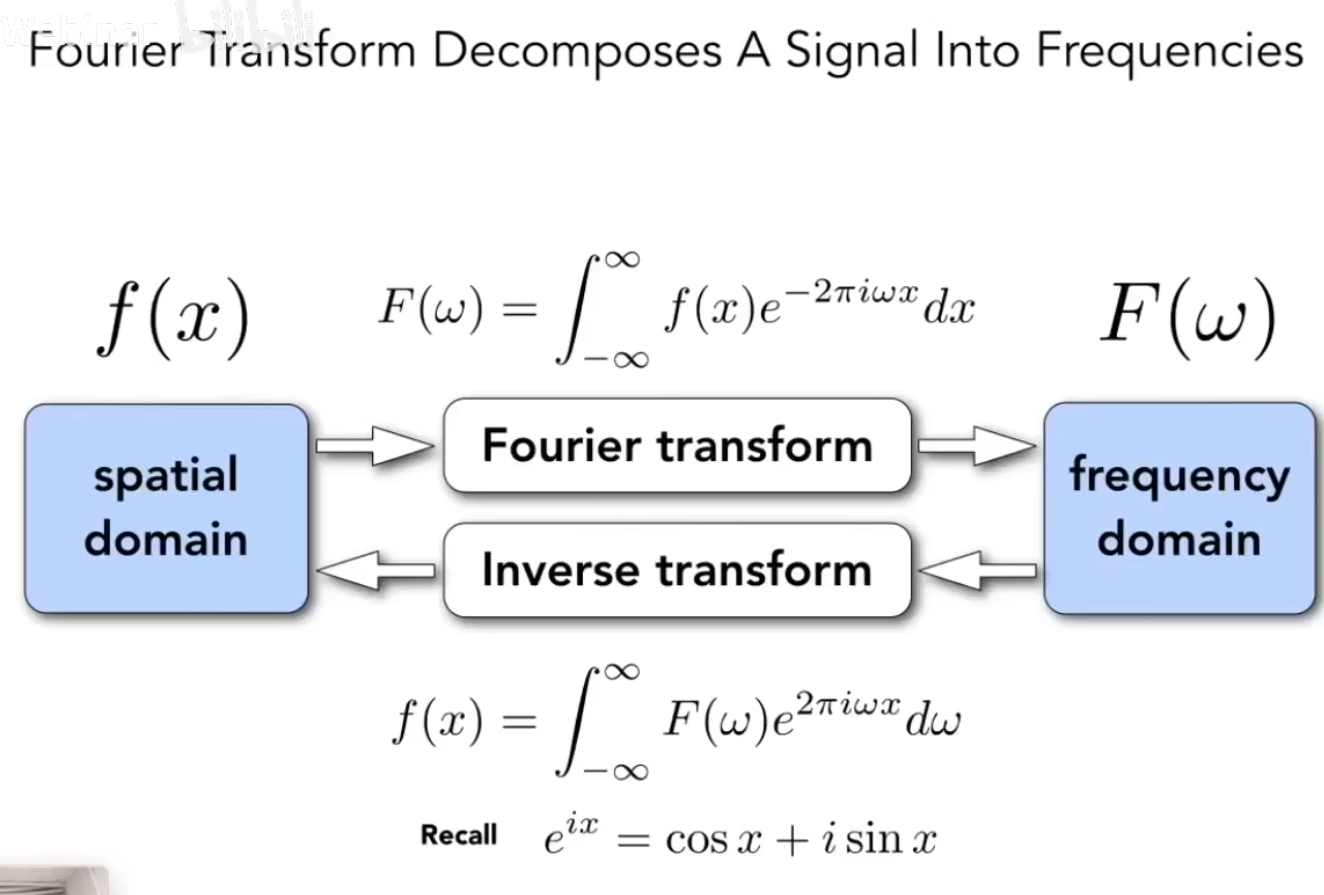
可以变来变去。

所谓傅立叶变换其实就是把函数给变成不同频率的段，并显示出来这些段。

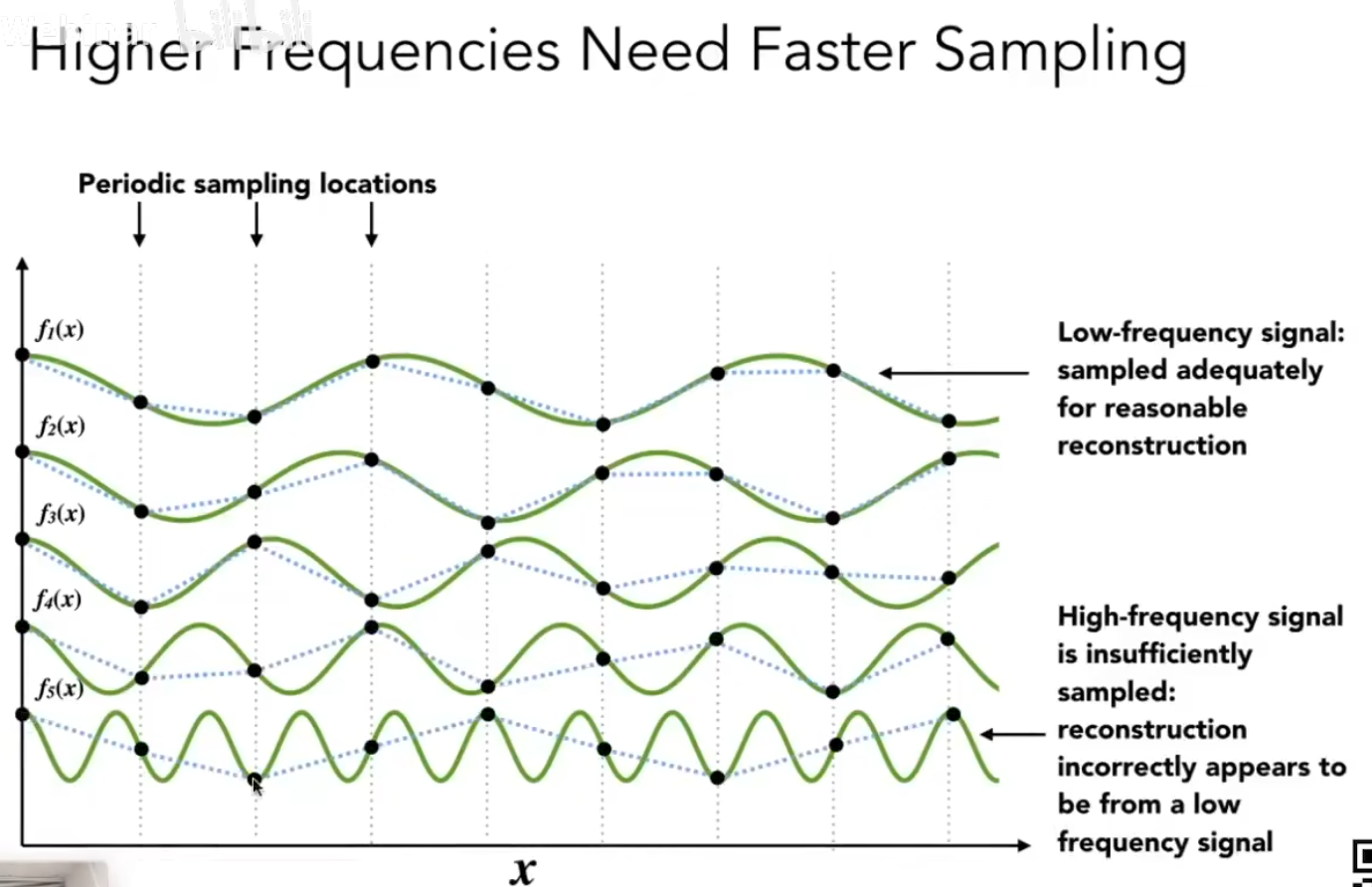
sampling采样已经大变样了，会出现失真问题。通过采样点很难恢复为原来的函数。
对于一个函数来说，它本身应该有的频率。采样也应该有一个频率。
如果这个函数的频率大于采样频率，就会像这样出现各种alising 错误。

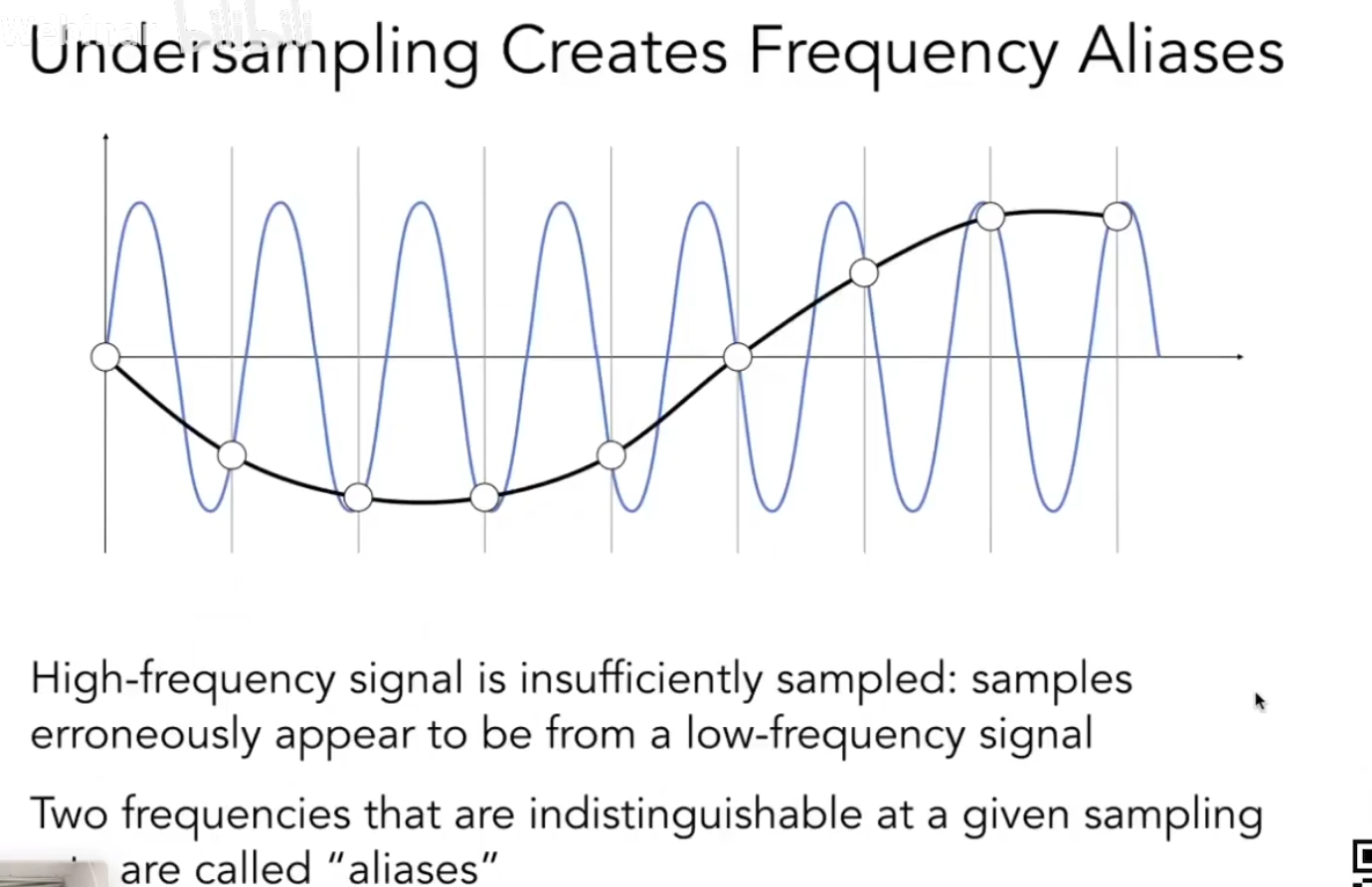
用同样的一个采样方法（频率）去采用频率截然不同的两种信号， 结果可以是完全相同的。（采样蓝线和黑线都可以，无法区分到底是蓝线还是黑线）。这种可以称之为“aliases”.

Filtering滤波 = 抹除掉特定频率的信号。

傅立叶变换的本质：把一个函数从时域变成频域。

傅立叶变换都是高频信息比较少，低频信息比较多，而且集中在中心。因此中心点比较亮。

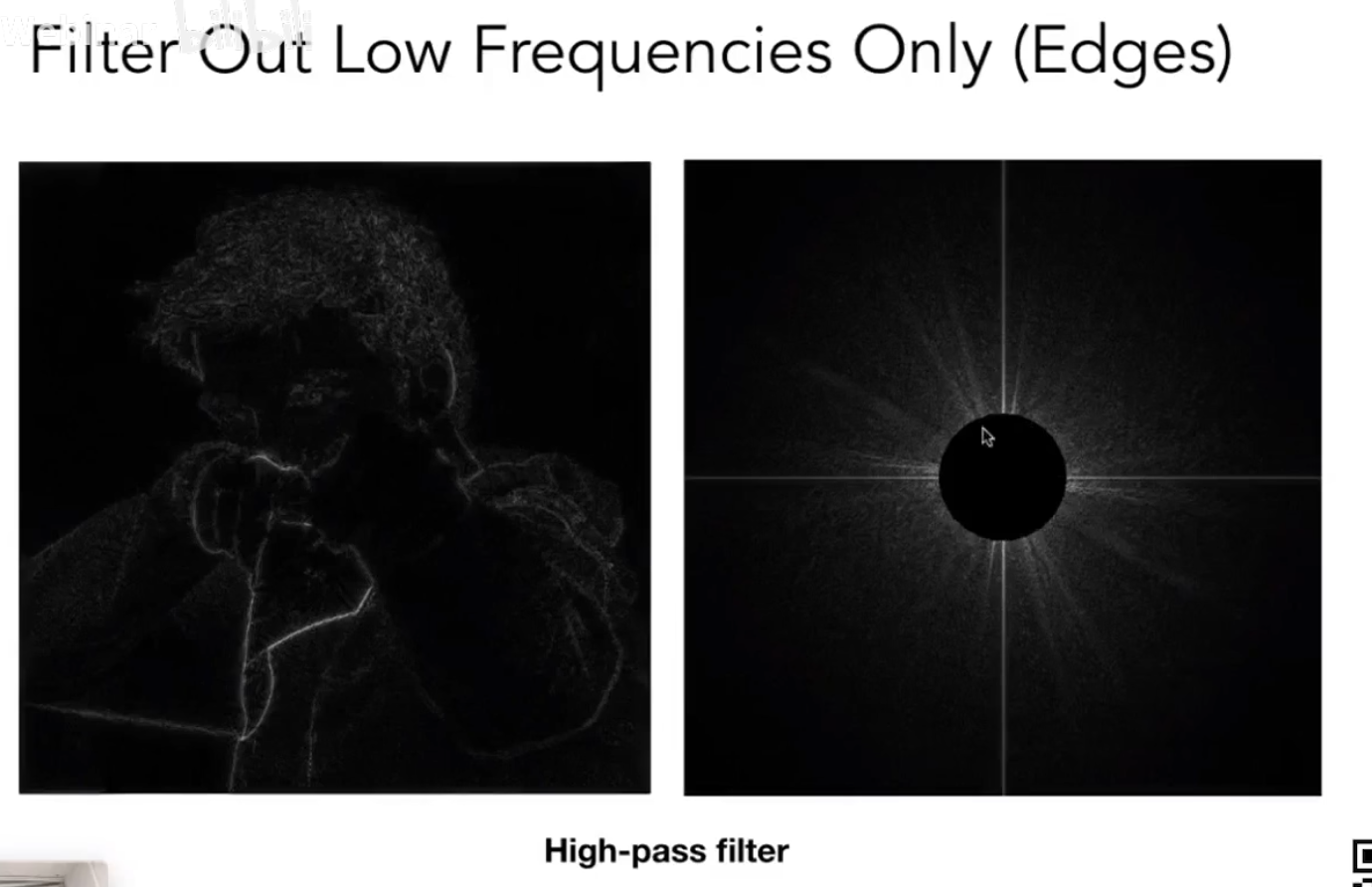
将低频信号进行屏蔽。只留下来高频的东西，这个高频的东西表示了图像内容的边界。屏蔽低频信号 = 提取图像内容的边界 => 高通滤波。

问：为什么高频信息就对应的图像的边界呢？
答：可以先定义一下我们如何判断什么是图像的边界，当我们发现一个区域的“上下左右”突然差距大了很多，那我们会说这个区域叫做边界。那信号变化特别大 其实就等于 高频的信号。

只留下了低频信息，会发现这个图片变模糊了。 相当于应用了低通滤波。

看频域图，发现去掉了高频信号，去掉了低频信号。 那就会提取到不那么明显的边界信息。

明白了这些，回到滤波， 刚刚说滤波=去掉特定频率信息。 另外一个角度来说 滤波 = 平均 = 卷积convolution。

卷积：如何卷积。其实也等于加权平均

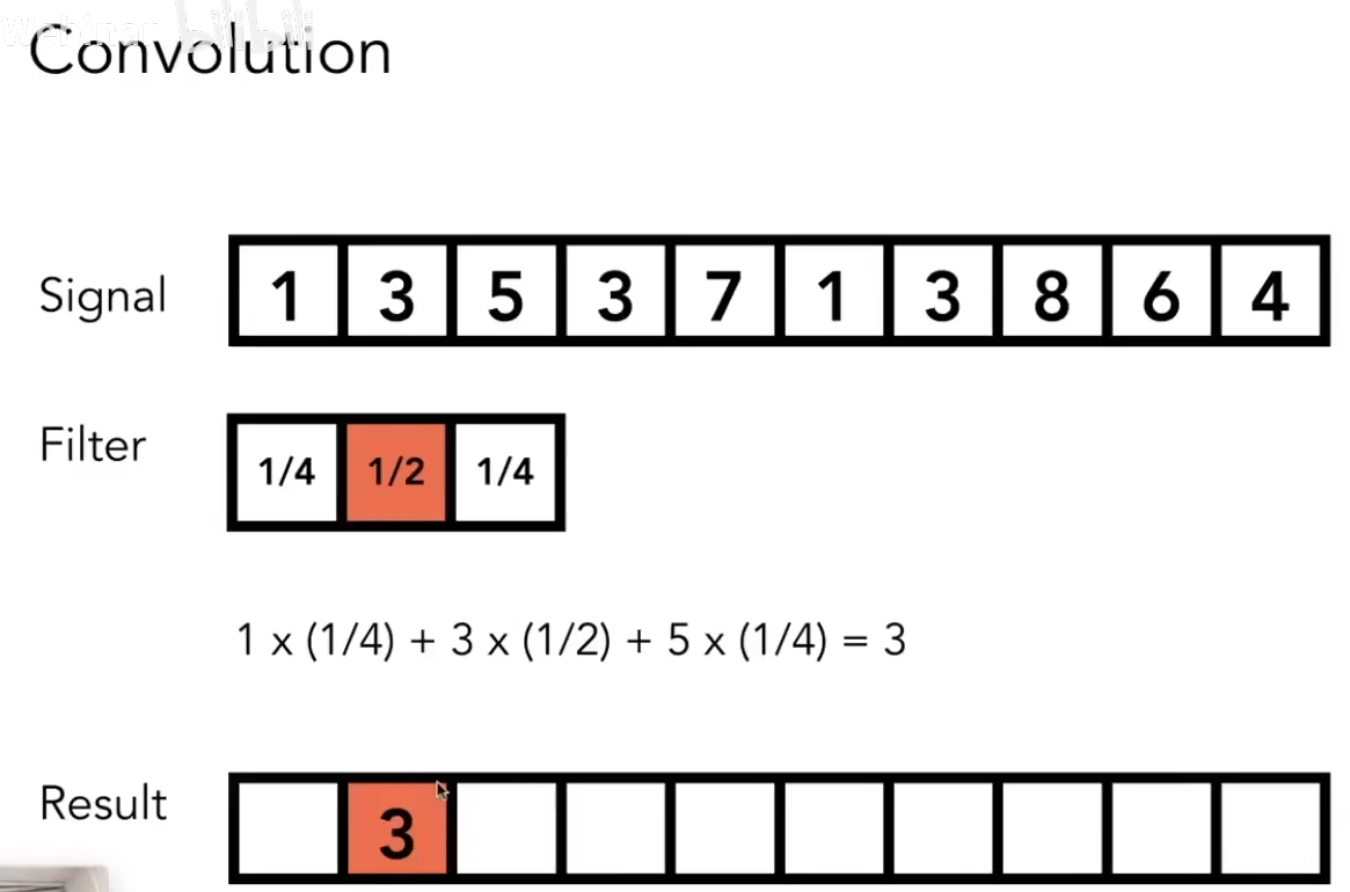
卷积定理：
在时域中卷积 等同于 在频域上的乘积

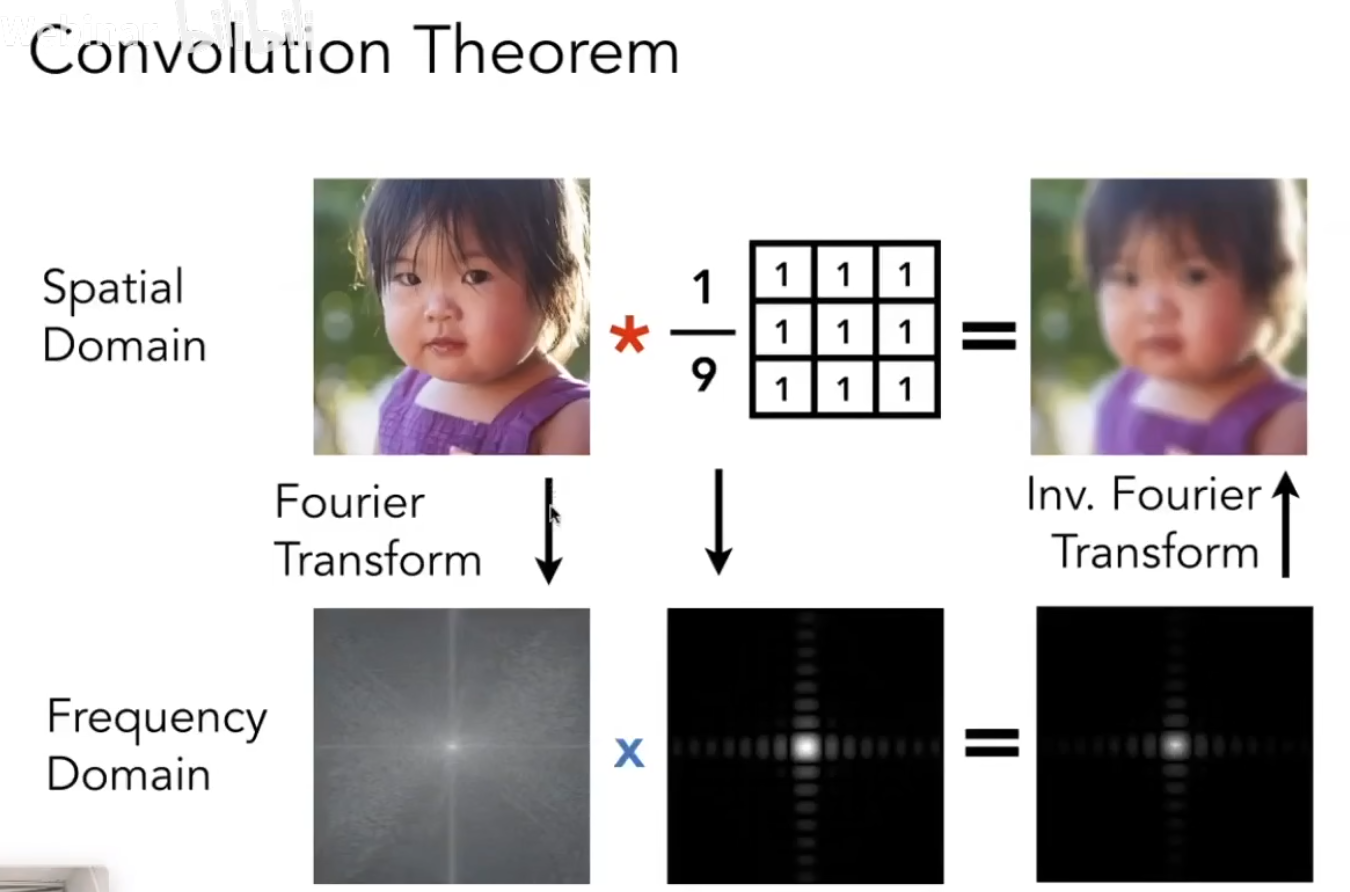
一张图在频域上直接求平均 = 一张图 先进行傅立叶变换到频域 然后做（平均的傅立叶变换）相乘 的结果 再傅立叶逆变换回去。

Box Filter 低通滤波器

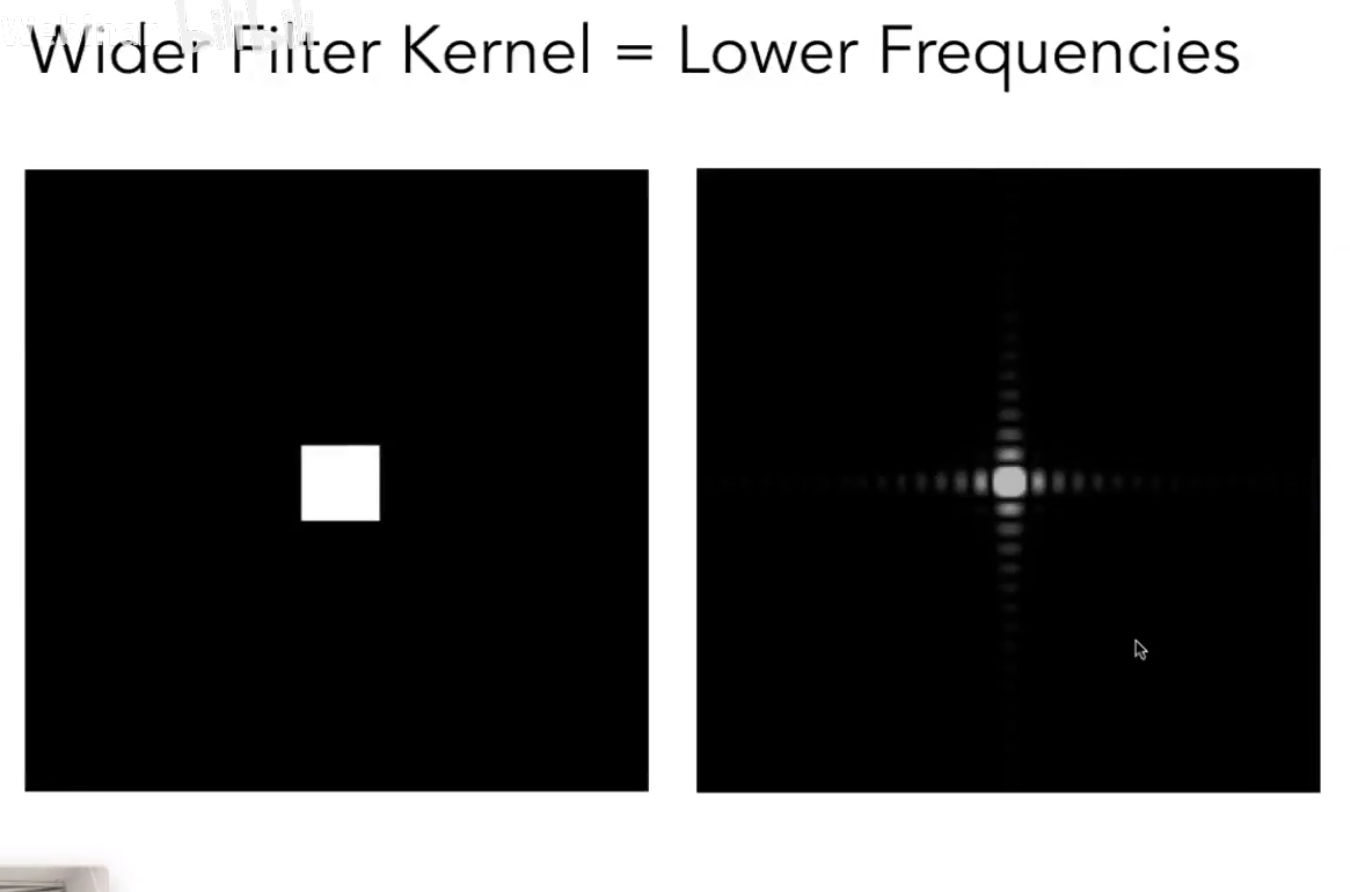
低通滤波器 通过的频率更大了一些之后，时域反而更小了，这是为什么呢？什么现象？

Sampling = Repeating

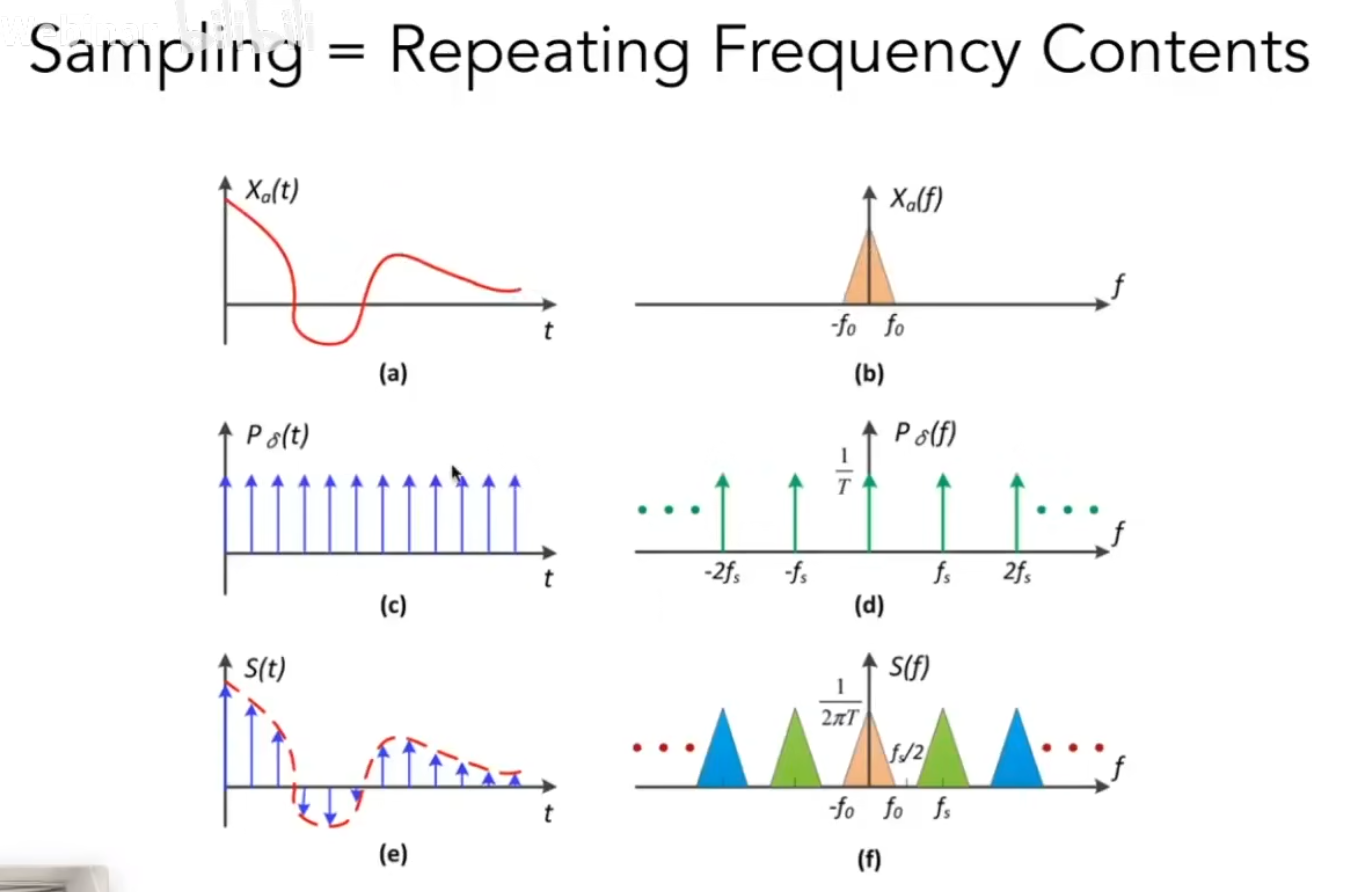
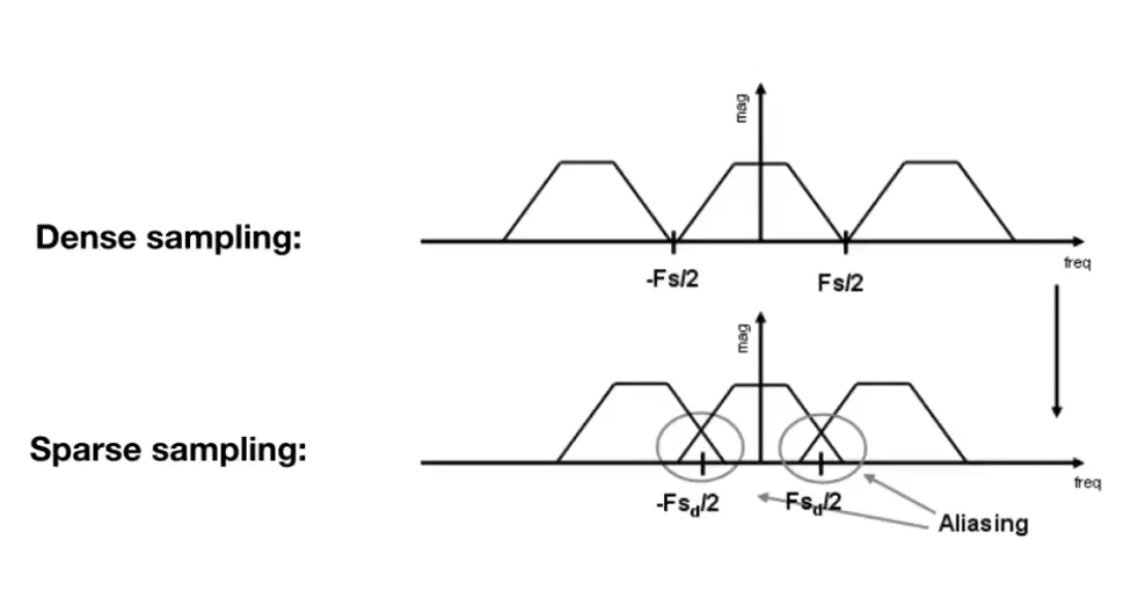
走样在频率的角度上来说，频谱在复制粘贴情况下发生了混合。

如何实现反走样：
1.增加采样率。选择参数牛逼的显示器，好的分辨率。
2.先做模糊，在做采样。也就是先把一个信号的高频信息拿掉，在做采样sampling。

究竟如何把三角形变成模糊的三角形。那我就用一个一定大小的低通滤波器对它进行卷积，就可以把他变成模糊的三角形。

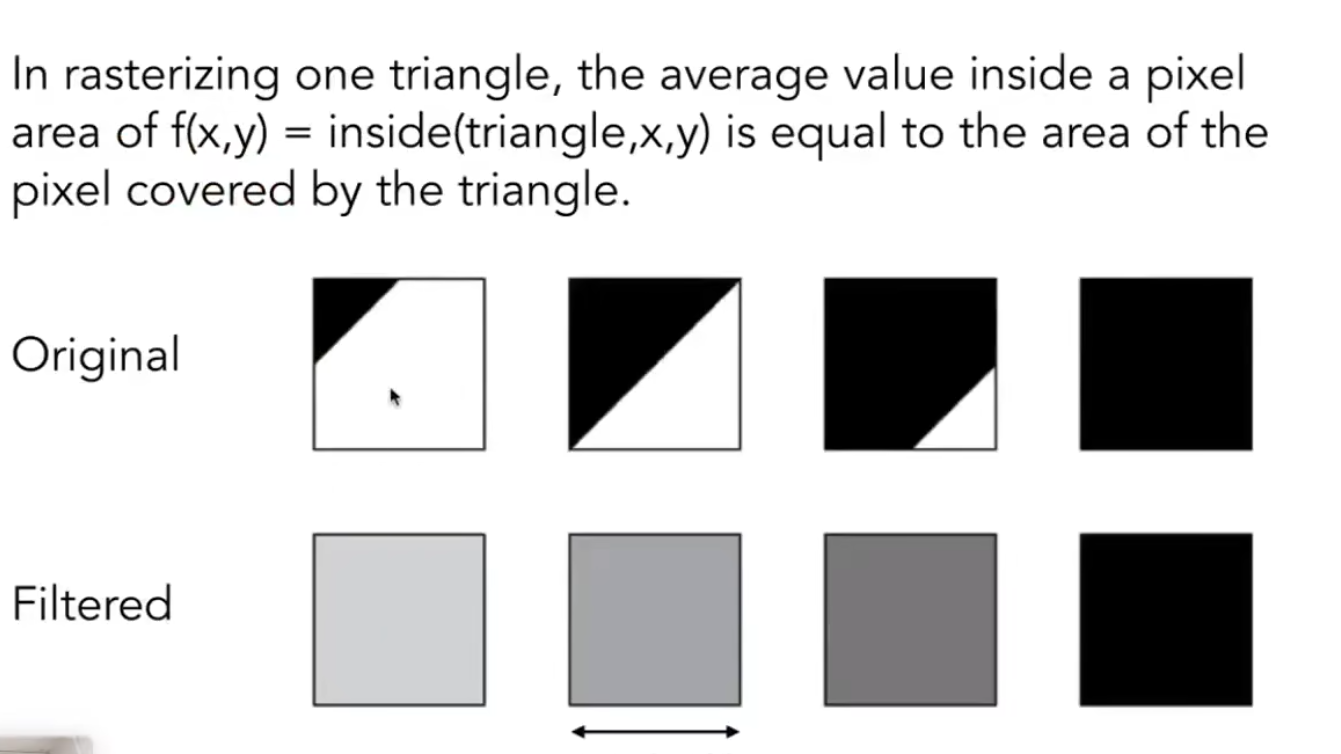
对覆盖面积求平均。若 三角形覆盖一个像素点越多，那这个区域就越黑。 （灰度值）
他提升了采样点采集频率，但是没有提高分辨率，计算多处理了，但是可以在同一块屏幕里面实现抗锯齿的效果。

工业界也用的 FXAA TAA
超采样 Super resolution ：DLSS（Deep Learning Super Sampling）