games101学习：Lecture 04 Transformation cout

Announcement:首先，先去写homework0，这节课会很难QAQ。

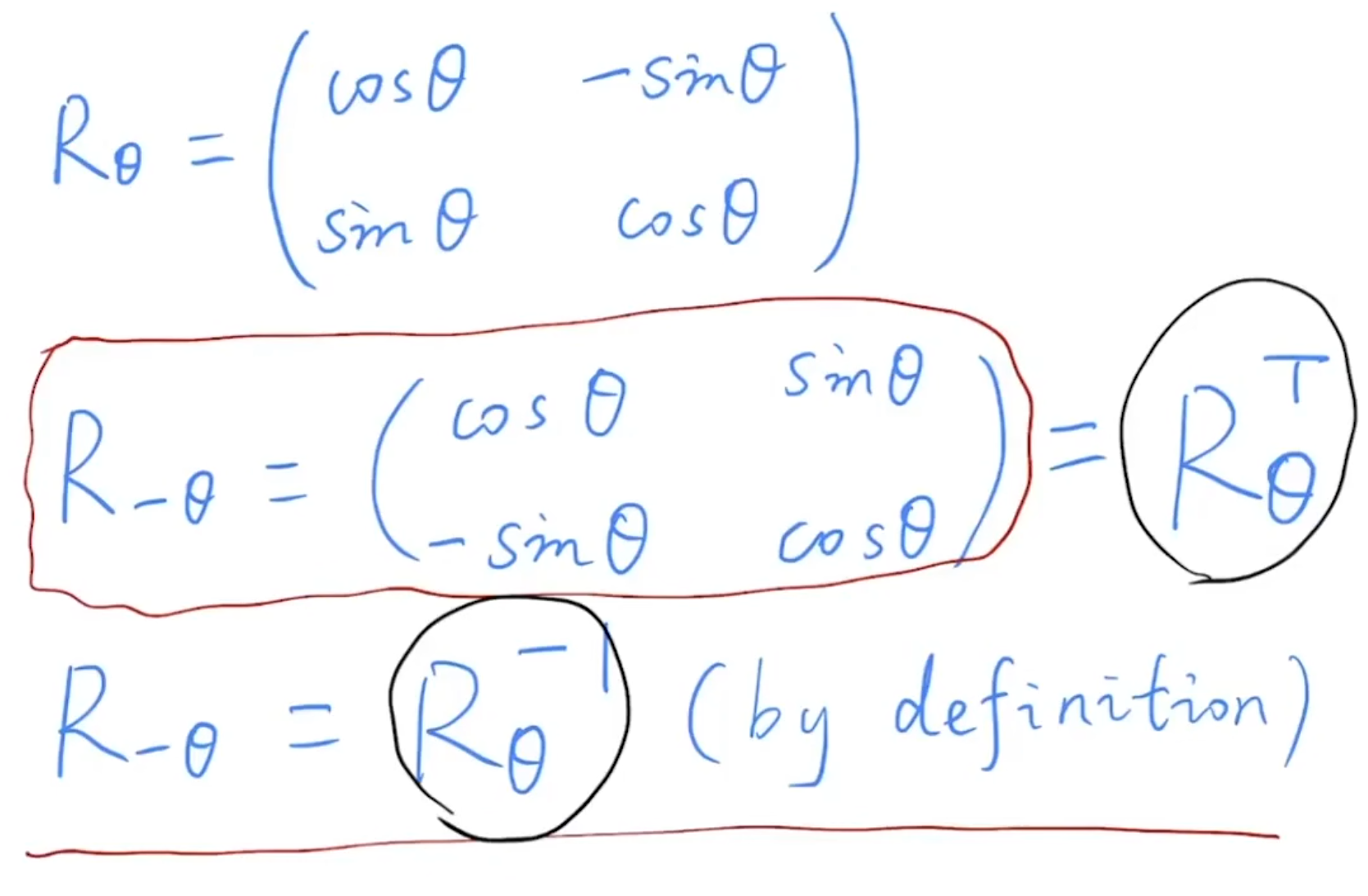
旋转矩阵有这样一个性质,旋转负theta角度和旋转theta角度的逆 其实是一样的。
旋转矩阵的逆 = 旋转矩阵的转置。

今天的内容主要包括视图view和投影变换，一点点的三维变换。

其中投影包括 正交 和 透视。

3D变换，绕着x，y，z轴进行旋转。

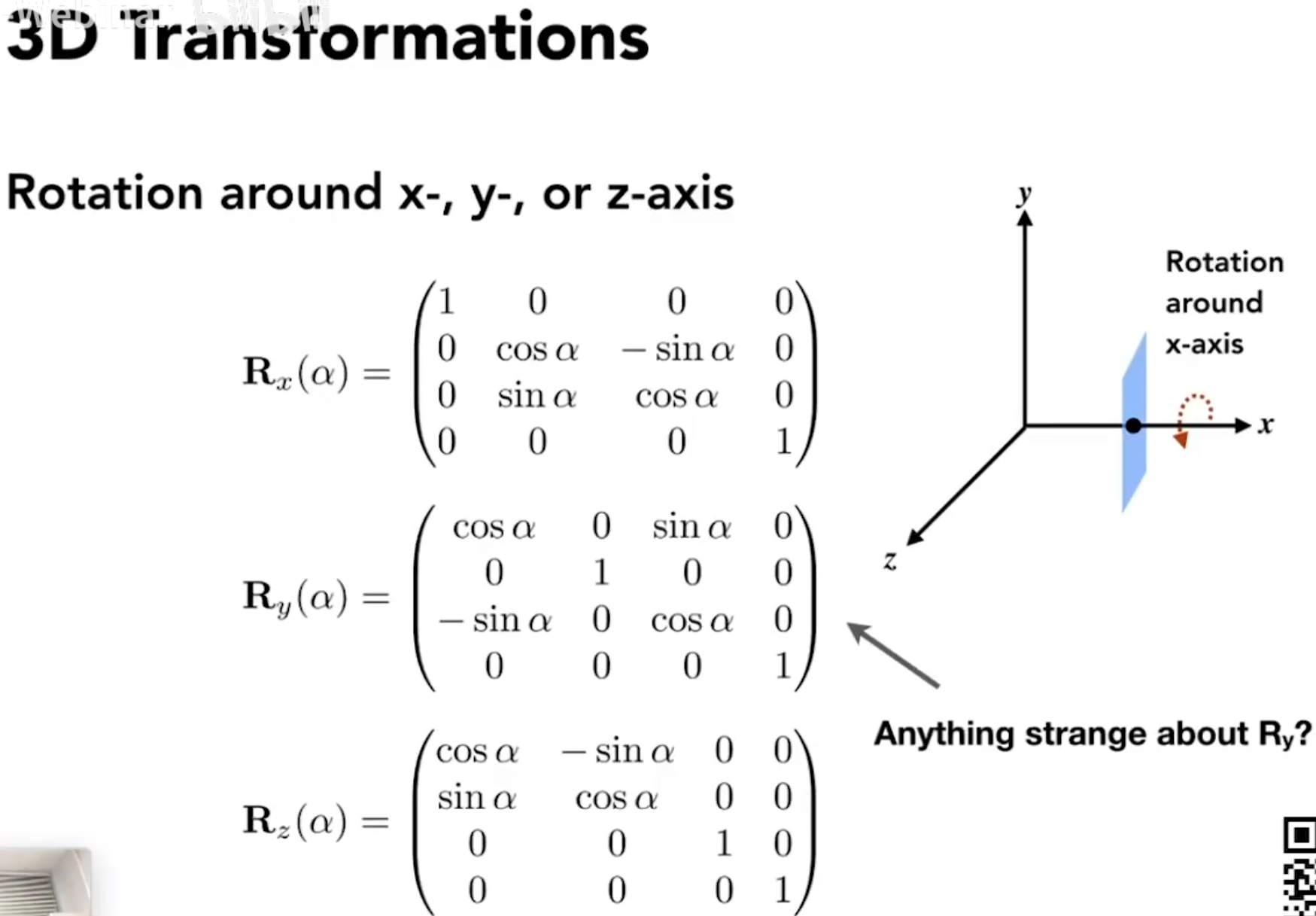
注意Ry的旋转有些许不同，Rx和Rz都和二维的变换非常的像。为什么呢？
和*面直角坐标系有关。
这是关键：绕 y 轴旋转是在 xz *面 上旋转，但注意在右手坐标系中，从 y 轴正方向看向原点，x 轴向右，z 轴向外（朝向观察者）。

此时旋转正方向（右手定则）与二维中的“x 向右，y 向上”情况坐标对应关系不同：

在二维旋转中，正角度是 从 x 轴转向 y 轴。在 xz *面中，如果保持“x 向右，z 向上”的类比，那么正旋转方向是 从 z 轴转向 x 轴（顺时针），而数学上我们希望正角度是 从 x 轴转向 z 轴（逆时针）。这导致了公式中 sin⁡α的符号需要交换位置（实际上是转置关系）来保持一致的物理旋转方向。

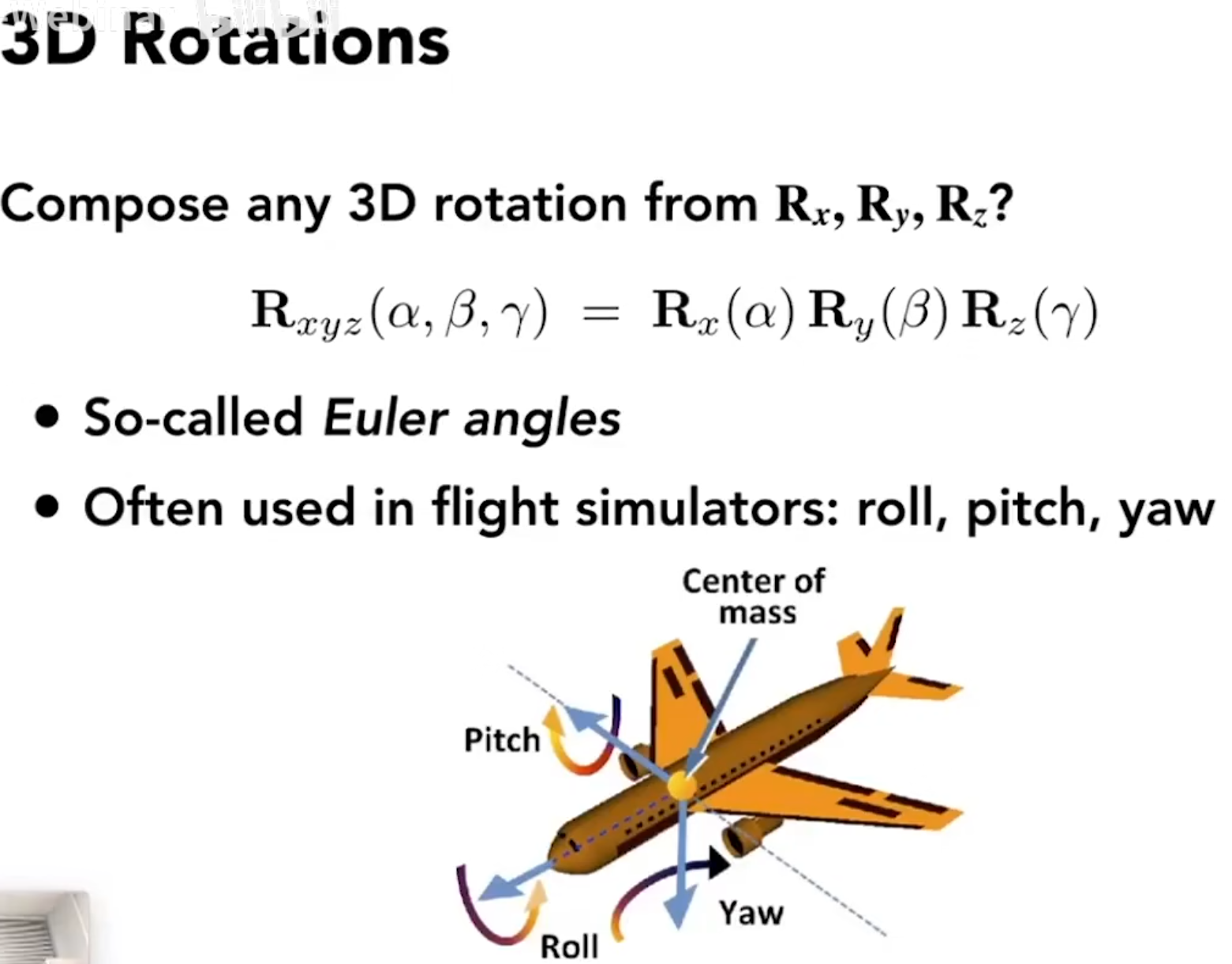
复杂的，绕任意轴的旋转都可以分解为多个绕x，y，z轴的旋转。

图形学中有人发明了一套办法，叫做Rodrigues' Rotation Formula罗德里格斯旋转公式,可以将任意的旋转写为矩阵。

通过任意的旋转分解为三个绕着x,y,z轴旋转来。

如何推导的呢？ https://www.cnblogs.com/wtyuan/p/12324495.html

后续推导：

思想：绕着某一个点n旋转某一个角度a。先将那个点*移到原点，再进行旋转，再进行逆*移回去。

View/Camera Transformation

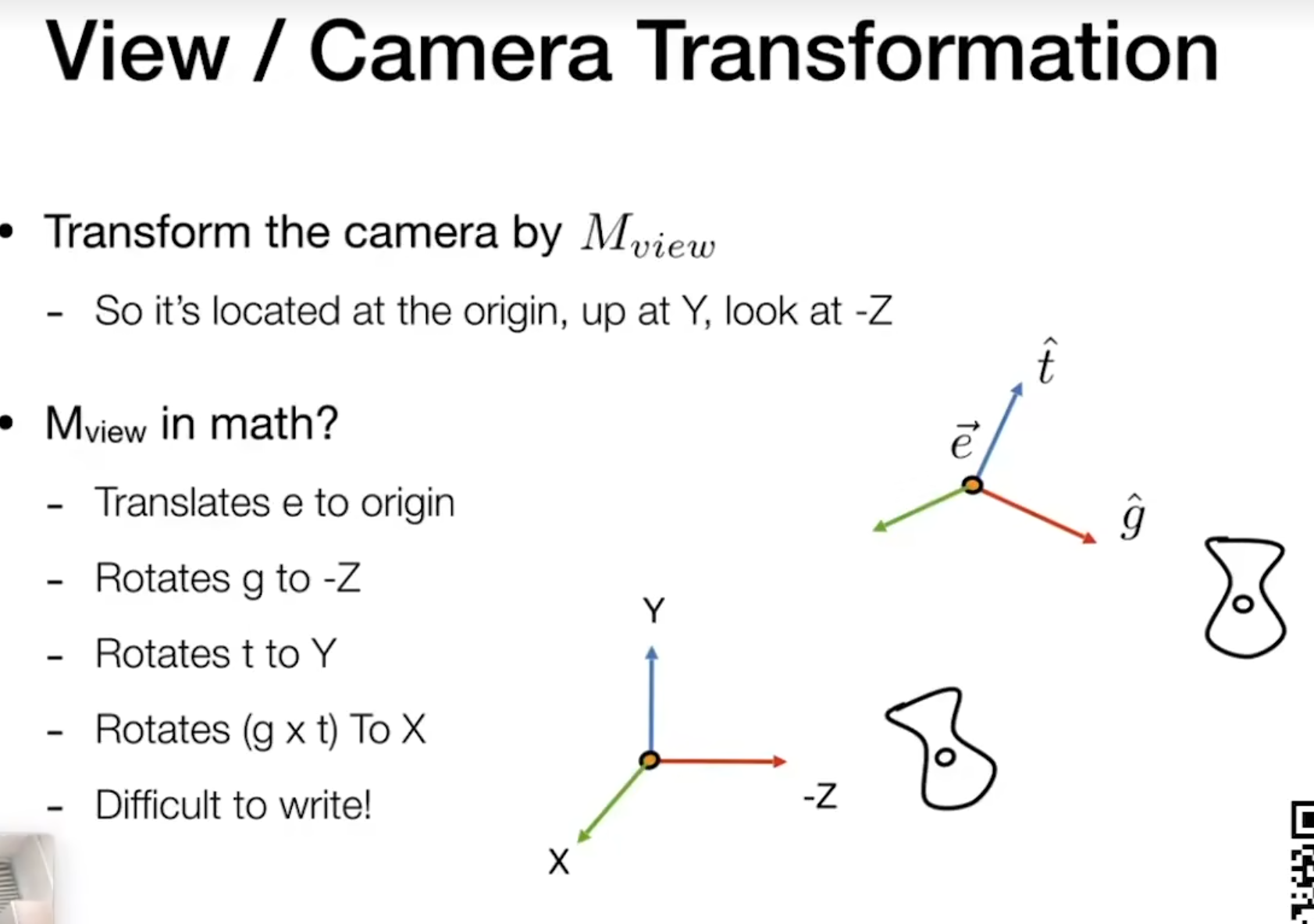
将摄像机从" e t g " 转换为 " x y z"，怎么从数学上来表达呢？
先将这个点移动到原点的地方去，*移量是(-x,-y,-z)。*移之后再考虑旋转

先进行*移再进行旋转，因此有Miew = Rview * Tview

这个旋转矩阵是一个正交矩阵（为什么？），其性质有正交矩阵的逆矩阵同时也是转置矩阵
为什么：

概念：MVP（Model View Projection）

投影变换（Projection transformation）
-Orthographic projection 正交投影 一般用来工程制图
-Perspective projection 透视投影 一般用来画画，给人一种*大远小的感觉

为什么会产生正交投影 和 透视投影的概念，一个是点，一个是*面图。

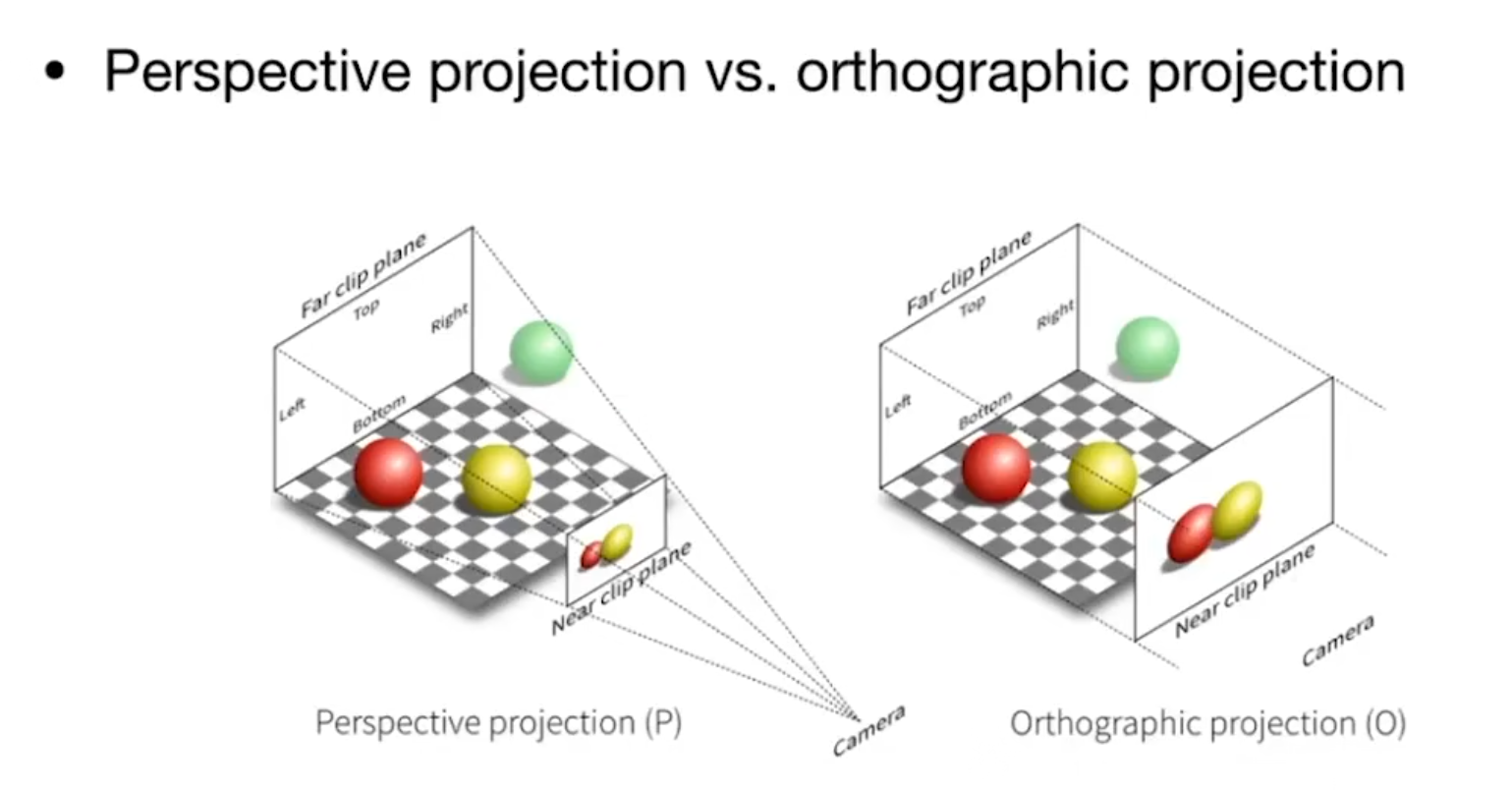
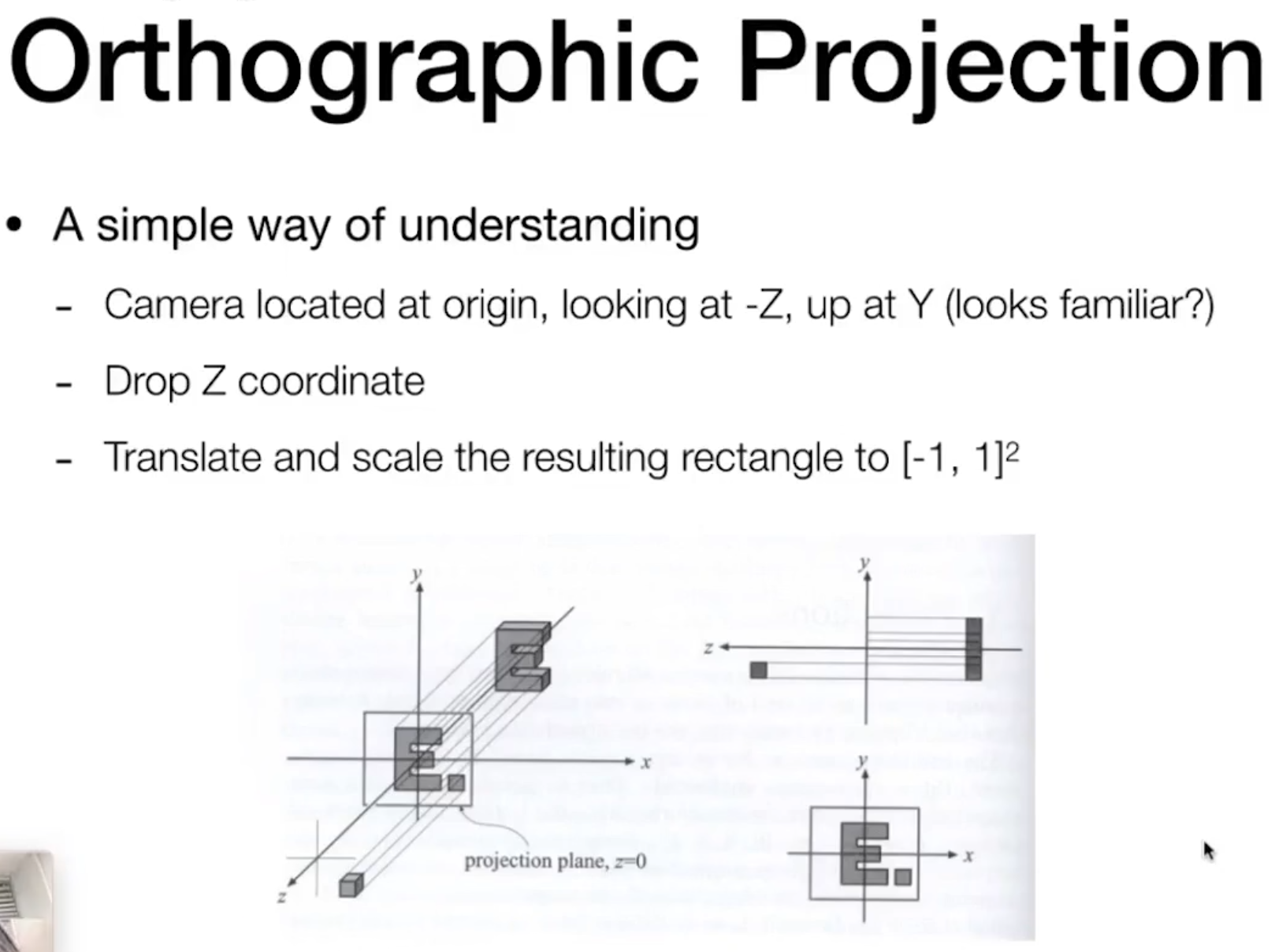
正交透视，能够把z轴的信息过滤掉，坏处就是难以看到物品的前后位置。

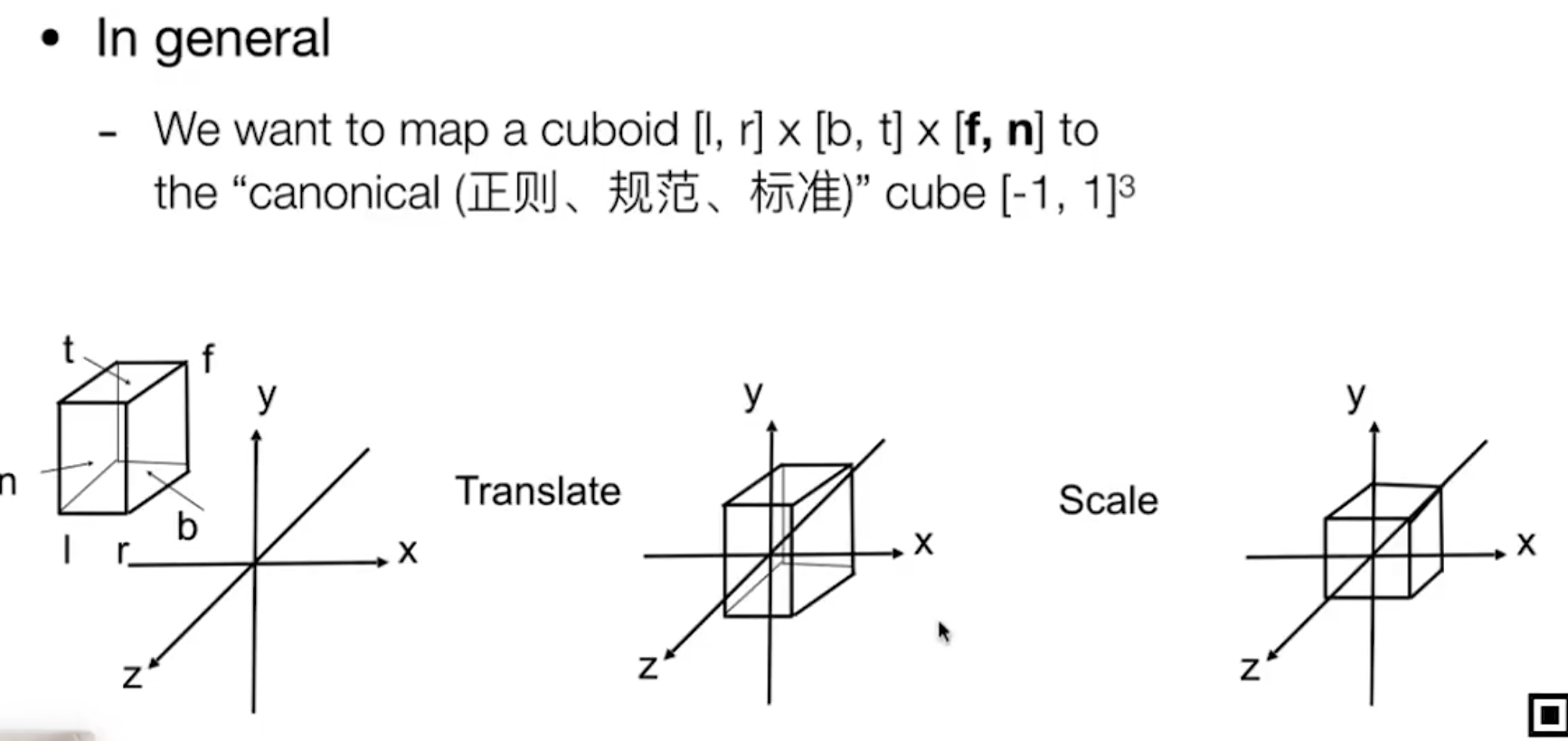
通常来说，将一个长方体 映射 为 一个标准立方体。
步骤1.放到坐标系中。 2.缩放变成标准1的 则变成了一个立方体。

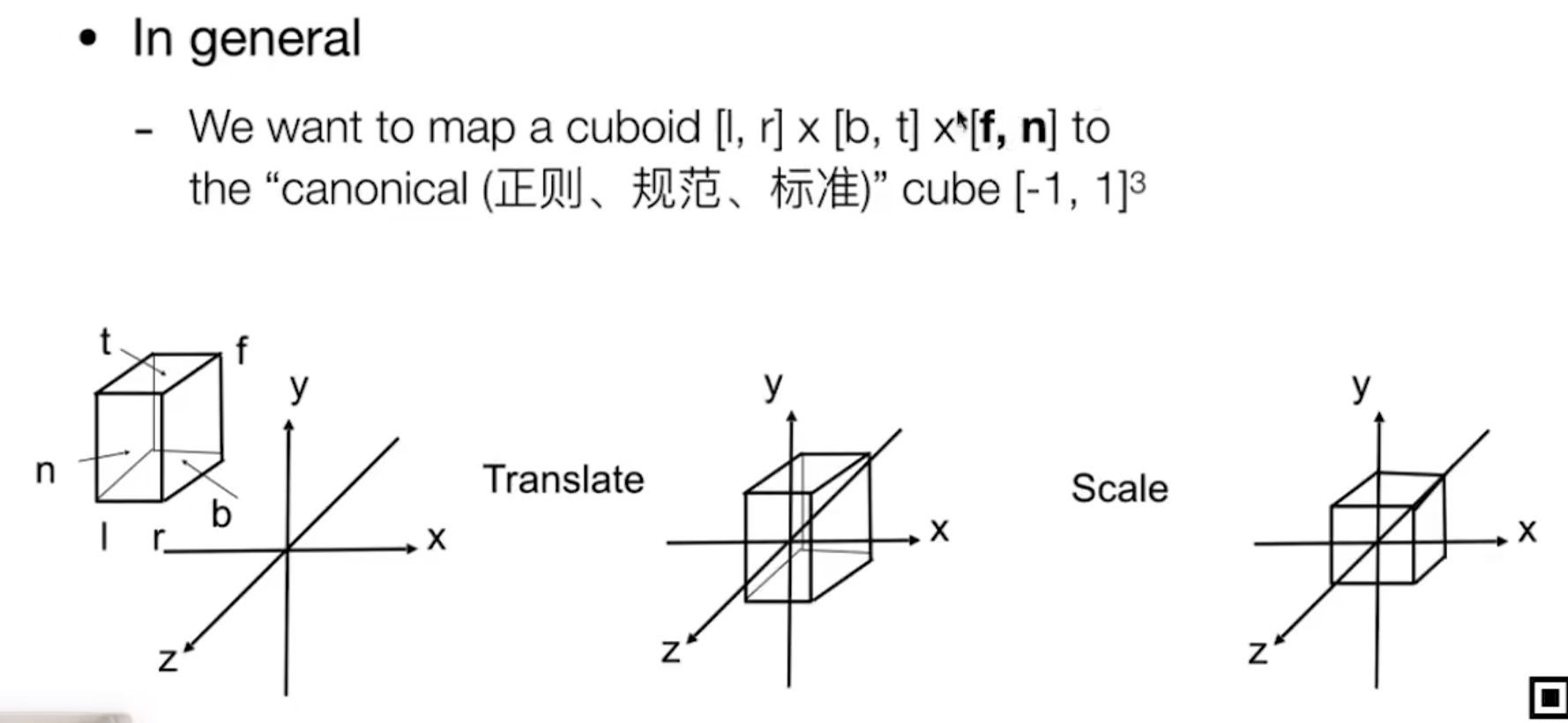
一个比较有意思的是，这里的字母f和n的意思是fast 和 next。 但是由于我们的摄像机视角是-z，因此其实f(远) 是小于 n(*)。

将这个变换写以矩阵的形式写出来。

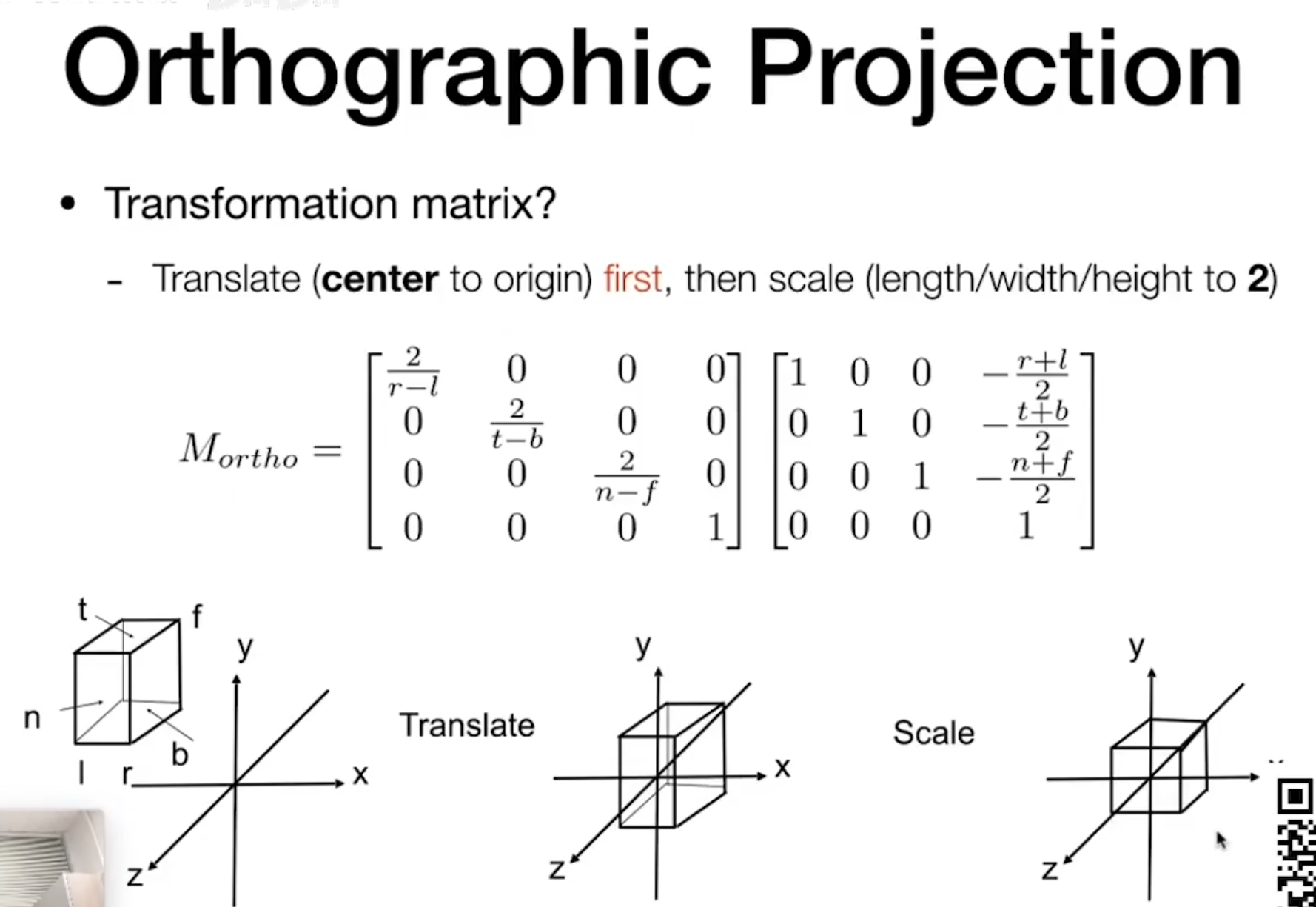
先进行位移，然后在进行scale变换。

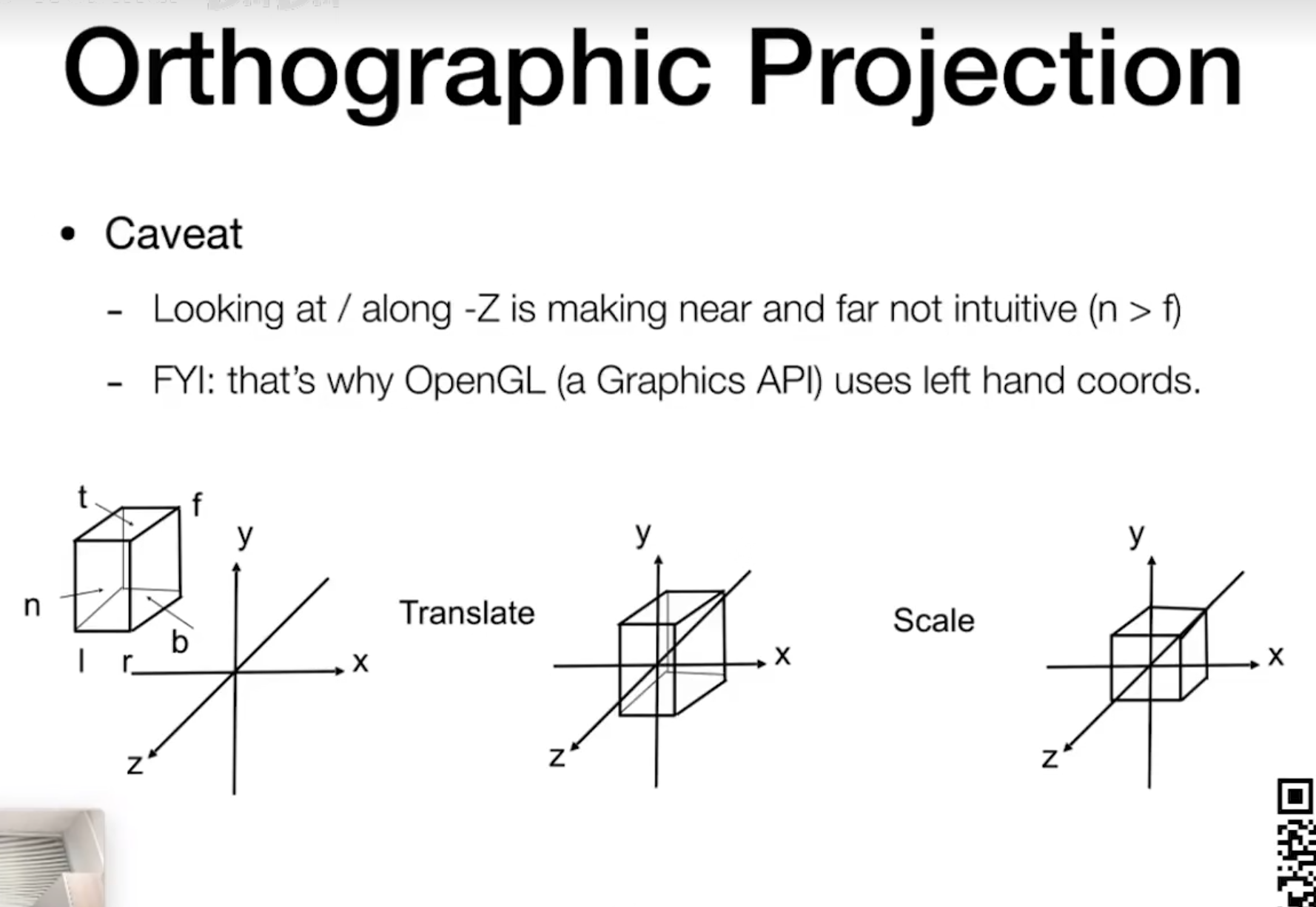
刚刚说了，由于我们是从-z的方向看过来的，因此 f < n 。这就是为什么OpenGL的API使用作左手坐标系以达成f > n的效果。

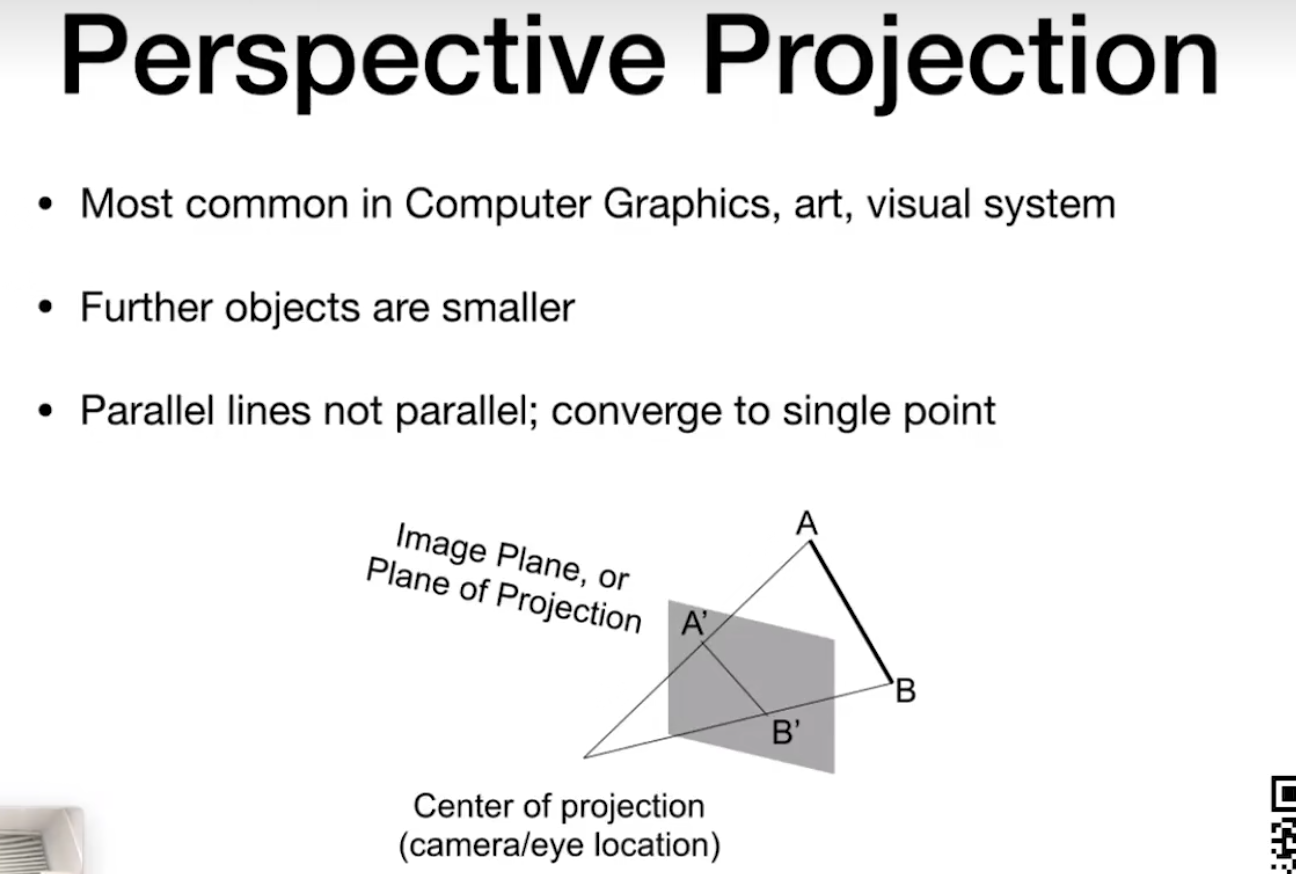
透视投影(Perspective Projection)

之前说的(x,y,z,1) 全部都 k(k不等于0) 得到(kx,ky,kz,k != 0) 或者甚至 * z(xz,yz,z*方，z != 0) 都是在三维空间中表示同一个点。（z要干嘛？）

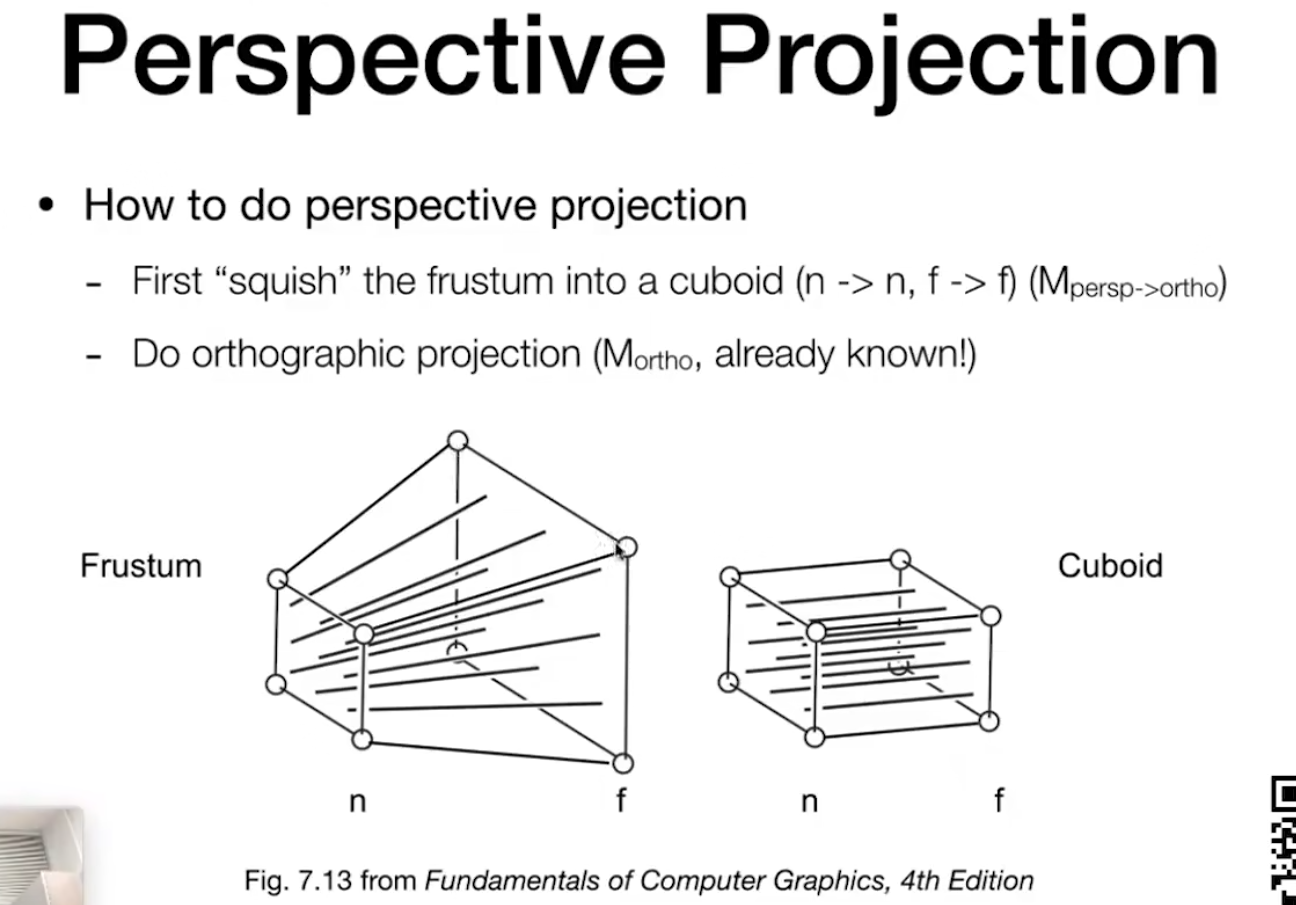
如何理解？ 很多图形学教材硬生生把透视投影写为数学公式，写一个矩阵出来，不太好理解。可以假设拿着一个远*面，这个远*面上有四个点。我们强行的把这四个点挤到*小*面去。那此时就挤成了一个空间中长方体。之后再经过正交投影到**面上去了。 总结下来就两步，第一步，先将Frustum的长方体挤成一个长方体，然后再做一次正交投影。

如何 挤
首先规定*** 远 *面 和 中心 **永远不变。

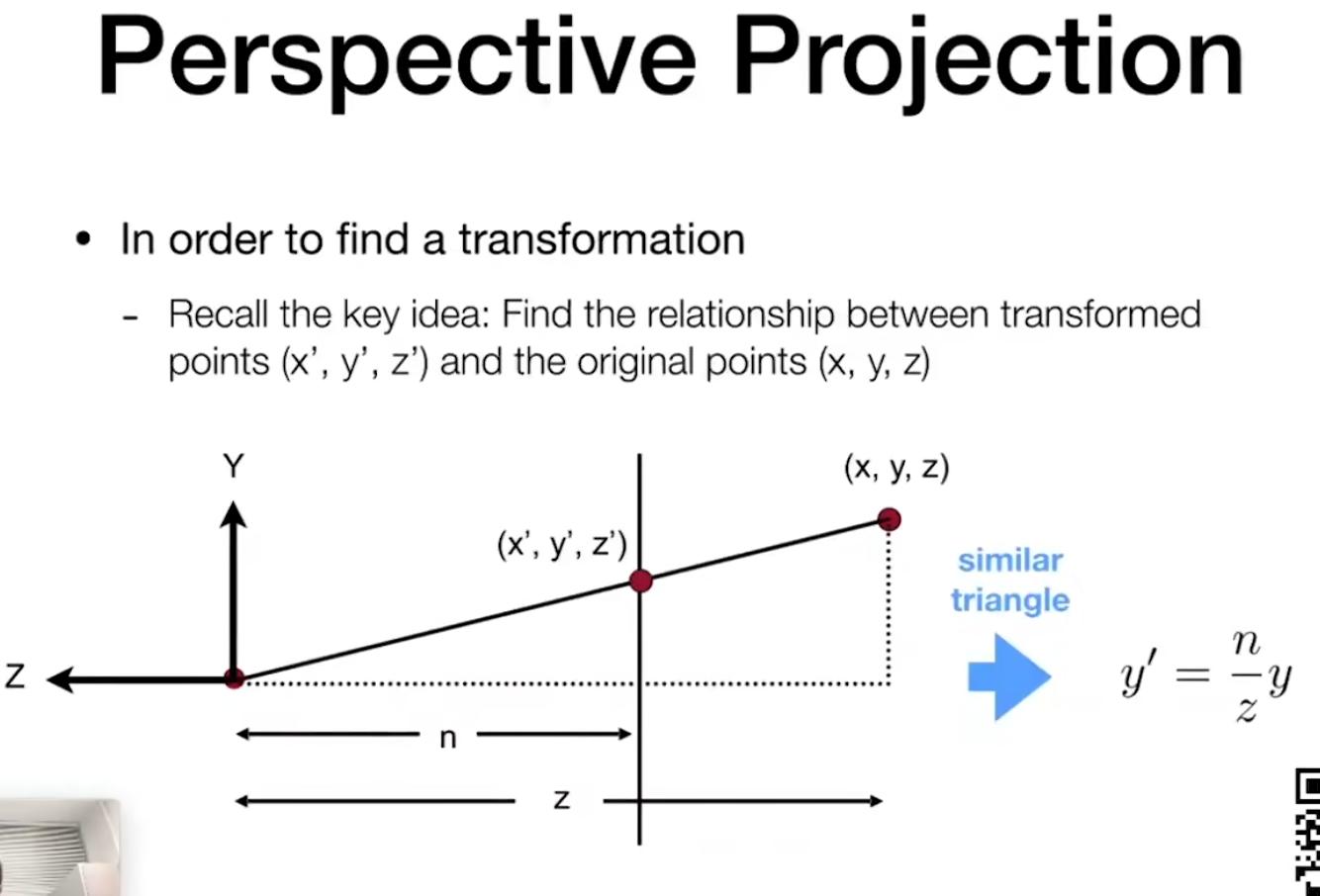
根据 相似三角形 来理解，很好理解。

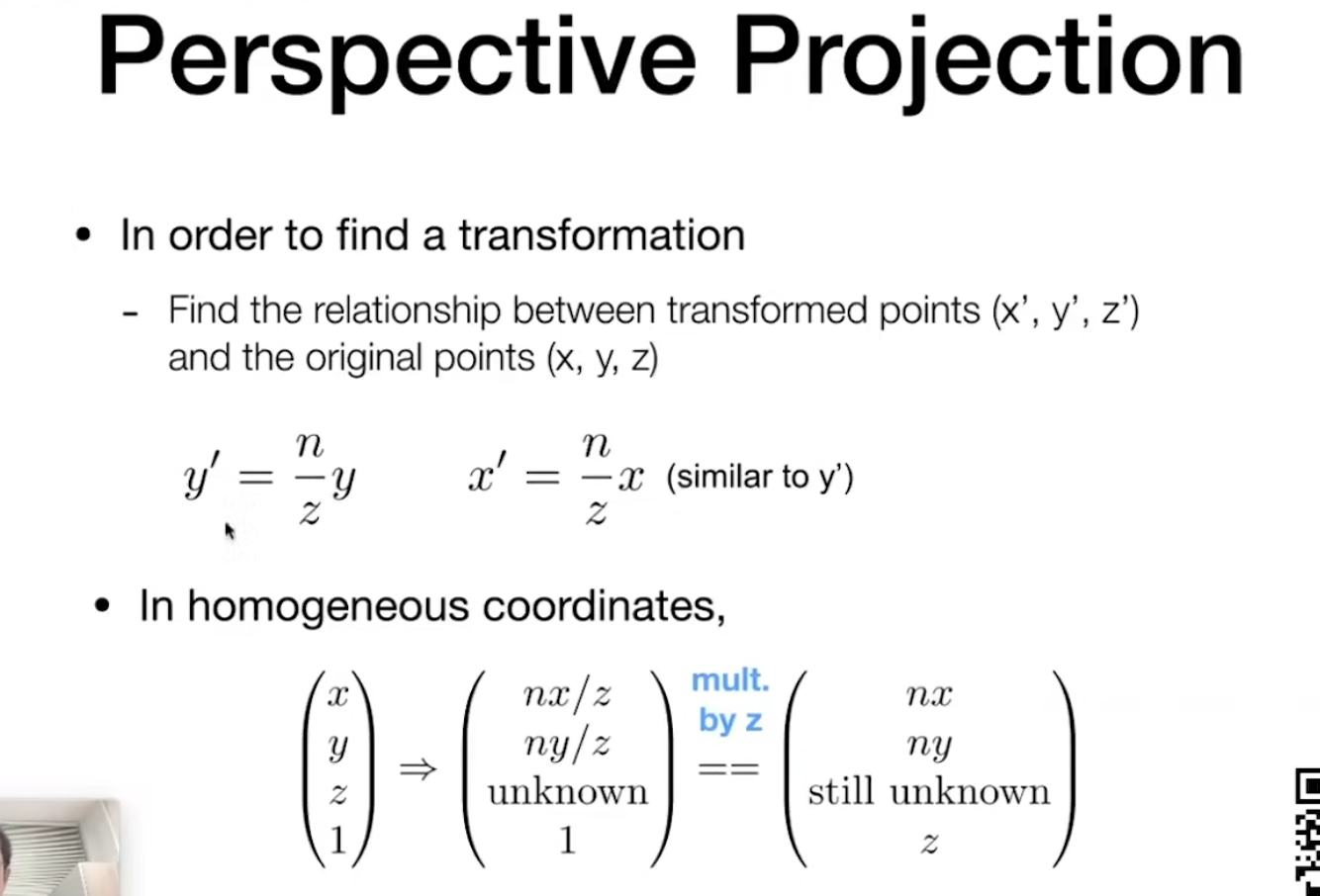
有两个小的观察

1. 任何一个点在**面上都不会发生变换。
2. 任何一个点的z在远*面上都不会发生变换。

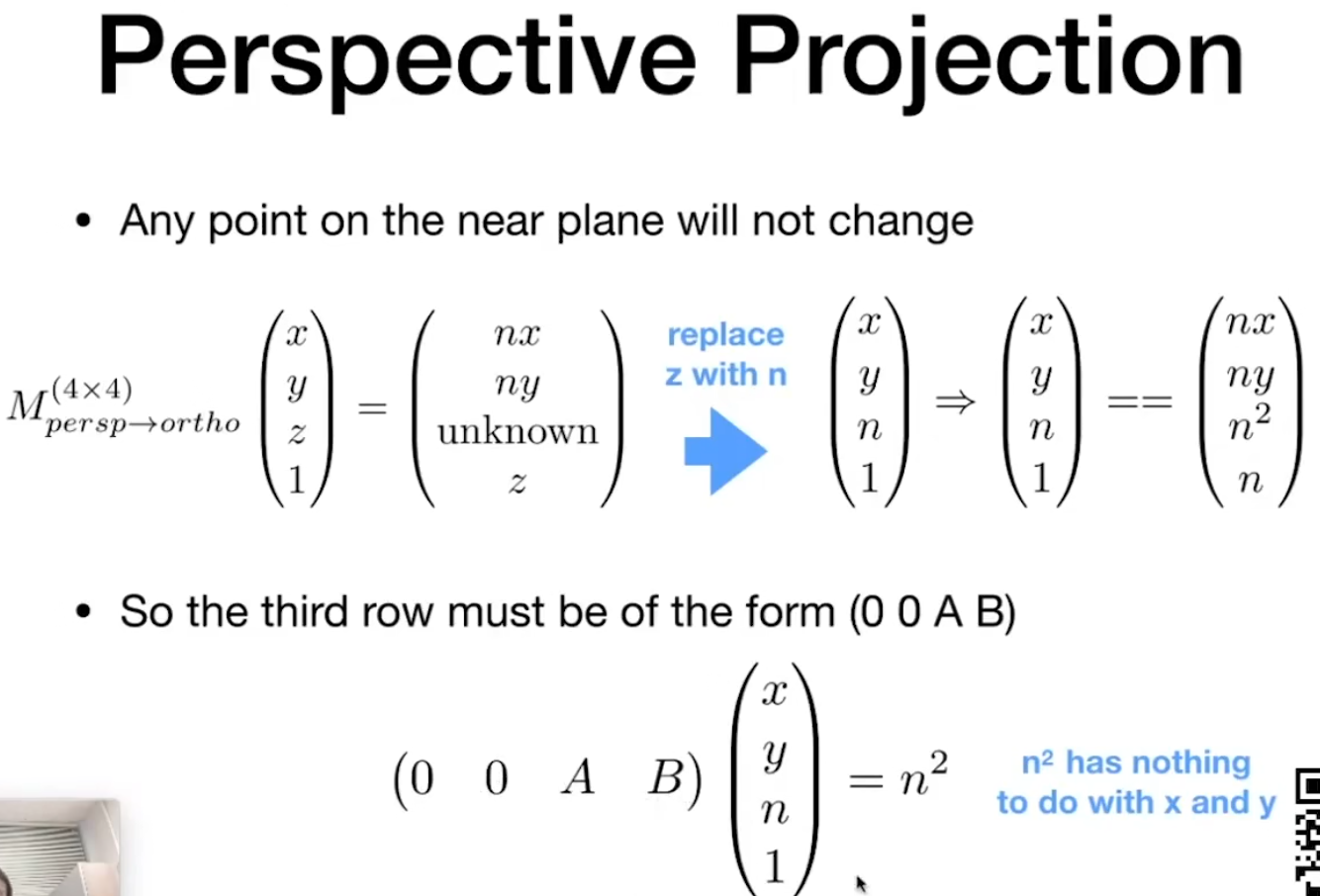
这里用了性质1，还有性质2呢。

留下一个问题： 我们说**面和远*面的z不会发生改变，那不在**面和远*面的点的z值如何变换呢？