基于Newmark-β法的单自由度体系地震响应MATLAB实现
基于Newmark-β法的单自由度体系地震响应MATLAB实现
一、算法原理与公式
单自由度体系运动方程:
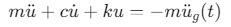
Newmark-β法递推公式:
-
预测步:
![]()
-
校正步:
![]()
二、MATLAB核心代码实现
function [time, disp, vel, acc] = Newmark_SDOF(m, c, k, ag, dt, beta, gamma, u0, v0)
% 参数说明:
% m: 质量 (kg)
% c: 阻尼系数 (N·s/m)
% k: 刚度 (N/m)
% ag: 地震加速度时程 (m/s²)
% dt: 时间步长 (s)
% beta, gamma: Newmark参数
% u0, v0: 初始位移和速度
n = length(ag);
time = 0:dt:(n-1)*dt;
% 初始条件
u = zeros(n,1); v = zeros(n,1); a = zeros(n,1);
u(1) = u0; v(1) = v0;
a(1) = (-m*ag(1) - c*v0 - k*u0)/m;
% 迭代计算
for i = 1:n-1
% 预测步
a_pred = a(i);
v_pred = v(i) + dt*(1-gamma)*a_pred;
u_pred = u(i) + dt*v_pred + 0.5*dt^2*(1-2*beta)*a_pred;
% 校正步
a(i+1) = (-m*ag(i+1) - c*v_pred - k*u_pred)/m;
v(i+1) = v_pred + dt*( (1-gamma)*a_pred + gamma*a(i+1) );
u(i+1) = u_pred + dt*v_pred + 0.5*dt^2*( (1-2*beta)*a_pred + 2*beta*a(i+1) );
end
% 输出结果
disp = u;
vel = v;
acc = a;
end
三、参数设置与优化
1. 典型参数组合
| 参数类型 | 推荐值范围 | 物理意义 |
|---|---|---|
| β | 0.20-0.30 | 位移滞后因子 |
| γ | 0.50-0.60 | 速度滞后因子 |
| 时间步长 | T/10 ≤ dt ≤ T/5 | T为结构自振周期 (s) |
2. 阻尼矩阵计算(瑞利阻尼)
function c = rayleigh_damping(m, k, xi, omega1, omega2)
% 输入参数:
% xi: 阻尼比
% omega1, omega2: 特征频率 (rad/s)
c = xi*m*2*omega1*omega2/(omega1+omega2);
end
四、测试案例(El Centro地震波)
% 参数设置
m = 1000; % 质量 (kg)
k = 25000; % 刚度 (N/m) → 自振周期 T=0.63s
xi = 0.05; % 阻尼比
dt = 0.01; % 时间步长
beta = 0.25; % Newmark-β参数
gamma = 0.5; % Newmark-γ参数
% 加载地震波(示例:El Centro NS分量)
ag = load('elcentro.txt'); % 假设数据格式为时间加速度
ag = ag(:,2); % 提取加速度列
% 运行算法
[time, disp, vel, acc] = Newmark_SDOF(m, rayleigh_damping(m,k,xi,0.1,10), k, ag, dt, beta, gamma, 0, 0);
% 可视化
figure;
subplot(3,1,1);
plot(time, ag*9.81, 'r', time, disp*1000, 'b--');
title('加速度时程对比 (m/s² vs mm)');
xlabel('时间 (s)'); ylabel('幅值');
legend('地震输入', '结构响应');
subplot(3,1,2);
plot(time, vel*100, 'g', time, acc, 'm:');
title('速度与加速度响应');
xlabel('时间 (s)'); ylabel('幅值');
subplot(3,1,3);
plot(disp, acc*1000, 'ko-');
title('位移-加速度滞回曲线');
xlabel('位移 (mm)'); ylabel('加速度 (m/s²)');
参考代码 采用Newmark法计算单自由度体系在地震作用下的响应 www.youwenfan.com/contentcnl/79193.html
五、结果分析要点
-
频谱特性验证:
[Pxx,f] = pwelch(disp,1024,512,1024,1/dt); figure; plot(f,10*log10(Pxx)); title('位移响应功率谱密度'); xlabel('频率 (Hz)'); ylabel('功率谱密度 (dB/Hz)'); -
关键指标计算: 最大位移:
max(abs(disp))等效阻尼比:通过能量等效法计算 周期偏移:对比初始周期与响应周期


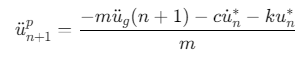
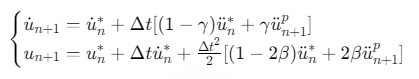

 浙公网安备 33010602011771号
浙公网安备 33010602011771号