MATLAB实现蜻蜓优化算法
MATLAB实现蜻蜓优化算法(Dragonfly Algorithm, DA)
一、算法原理与核心机制
1. 生物行为建模
蜻蜓算法模拟蜻蜓的以下自然行为:
-
分离(Separation):避免个体碰撞,公式为:
![]()
-
对齐(Alignment):个体速度与邻居平均速度一致:
![]()
-
凝聚(Cohesion):向群体中心靠拢:
![]()
-
食物吸引(Attraction):向最优解移动:
![]()
-
天敌逃避(Repulsion):远离最差解:
![]()
2. 算法流程
-
初始化:随机生成蜻蜓群体,设置参数(惯性权重、分离系数等)。
-
适应度评估:计算每个个体的目标函数值。
-
行为更新:根据分离、对齐、凝聚、食物和天敌力更新位置:
![]()
-
边界处理:限制个体在搜索空间内。
-
迭代终止:达到最大迭代次数或收敛条件。
二、MATLAB实现
1. 基本框架
function [best_solution, best_fitness] = DA(func, dim, lb, ub, max_iter, pop_size)
% 参数设置
w = 0.5; % 惯性权重
s = 1.5; % 分离系数
a = 1.5; % 对齐系数
c = 1.5; % 凝聚系数
f = 0.5; % 食物吸引系数
e = 0.5; % 天敌逃避系数
% 初始化种群
pop = lb + (ub - lb) .* rand(pop_size, dim);
fitness = arrayfun(@(i) func(pop(i,:)), 1:pop_size);
% 记录最优解
[best_fitness, best_idx] = min(fitness);
best_solution = pop(best_idx, :);
% 迭代优化
for iter = 1:max_iter
for i = 1:pop_size
% 计算群体行为
S = compute_separation(pop, i);
A = compute_alignment(pop, i);
C = compute_cohesion(pop, i);
[F, E] = compute_food_enemy(pop, i, best_solution);
% 更新位置
new_pos = w*pop(i,:) + s*S + a*A + c*C + f*F + e*E;
new_pos = max(min(new_pos, ub), lb); % 边界处理
% 更新适应度
new_fitness = func(new_pos);
if new_fitness < fitness(i)
pop(i,:) = new_pos;
fitness(i) = new_fitness;
if new_fitness < best_fitness
best_fitness = new_fitness;
best_solution = new_pos;
end
end
end
end
end
2. 关键函数实现
function S = compute_separation(pop, i)
% 分离力计算
neighbors = pop(1:i-1, :);
distances = pdist2(pop(i,:), neighbors);
S = sum((neighbors - pop(i,:)) ./ (distances.^2 + eps), 1);
end
function [F, E] = compute_food_enemy(pop, i, best)
% 食物与天敌选择
[~, best_idx] = min(arrayfun(@(j) func(pop(j,:)), 1:size(pop,1)));
[~, worst_idx] = max(arrayfun(@(j) func(pop(j,:)), 1:size(pop,1)));
F = best - pop(i,:);
E = pop(worst_idx,:) - pop(i,:);
end
参考代码 新型算法之蜻蜓优化算法 www.youwenfan.com/contentcni/64995.html
三、算法改进方向
1. 自适应参数调整
-
动态权重:根据迭代次数调整惯性权重:
![]()
-
邻域搜索:引入K近邻机制加速收敛。
2. 多目标优化扩展(MODA)
- 帕累托前沿维护:使用外部存档存储非支配解。
- 适应度分配:结合拥挤距离与目标函数值。
3. 混合策略
- DA-PSO融合:结合粒子群的全局搜索能力。
- DA-GWO混合:利用灰狼算法的包围机制。
四、应用场景与案例
1. 工程优化
-
结构设计:桁架优化(MATLAB案例):
% 目标函数:最小化重量+最大化刚度 func = @(x) 0.5*x(1)*x(2) + 100*(x(3)-0.5)^2; [x_opt, fval] = DA(func, 3, [0,0,0], [10,10,10], 100, 50);
2. 机器学习
-
超参数调优:优化SVM参数(C, gamma):
% 适应度函数:交叉验证准确率 func = @(params) svm_cv(params(1), params(2));
3. 路径规划
-
栅格地图导航:动态避障(MATLAB可视化):
% 伪代码:迭代更新蜻蜓位置,避开障碍物 while ~goal_reached for each dragonfly compute_repulsion_from_obstacles(); update_position(); end end
五、性能对比与参数设置
| 指标 | DA | PSO | GWO |
|---|---|---|---|
| 收敛速度 | 快(平均) | 中等 | 慢 |
| 全局搜索能力 | 强 | 弱 | 中等 |
| 参数敏感性 | 中等 | 高 | 低 |
| 适用维度 | 2-30 | 2-50 | 2-100 |
推荐参数:
- 种群规模:30-100
- 最大迭代:100-500
- 惯性权重:0.4-0.9
六、挑战与解决方案
| 挑战 | 解决方案 |
|---|---|
| 高维搜索效率低 | 引入降维技术(PCA)或子群划分 |
| 动态环境适应性差 | 结合强化学习动态调整参数 |
| 多模态问题收敛不稳定 | 改进外部存档管理策略 |
蜻蜓优化算法通过模拟自然行为实现了高效的全局搜索,在复杂优化问题中展现出独特优势。

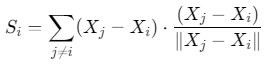
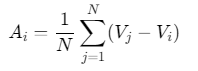
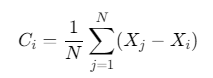
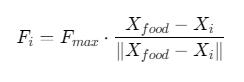
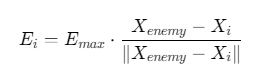
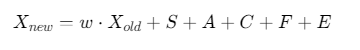
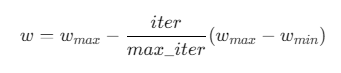

 浙公网安备 33010602011771号
浙公网安备 33010602011771号