基于TS模糊模型的倒立摆控制MATLAB实现
一、TS模糊模型控制原理
-
系统建模
倒立摆动力学方程:
![]()
其中,\(x\)为小车位移,\(θ\)为摆角,\(F\)为控制力,\(M\)为小车质量,\(m\)为摆杆质量。
-
TS模糊模型构建
-
输入变量:角度误差\(e=θ\),角速度误差\(e˙=θ˙\)
-
输出变量:控制力F
-
隶属函数:高斯型(前件)+ 线性函数(后件)
-
模糊规则:
Rule 1: IF e is NB and \dot{e} is NB THEN F=K1*e + K2*\dot{e} Rule 2: IF e is NS and \dot{e} is NS THEN F=K3*e + K4*\dot{e} ...
-
二、MATLAB/Simulink实现步骤
1. 系统参数定义
% 系统参数
M = 1.096; % 小车质量(kg)
m = 0.109; % 摆杆质量(kg)
l = 0.25; % 摆杆长度(m)
g = 9.81; % 重力加速度(m/s²)
J = 0.0034; % 摆杆转动惯量(kg·m²)
2. TS模糊控制器设计
% 创建模糊推理系统
fis = newfis('pendulum_TS');
% 输入变量定义
fis = addvar(fis,'input','e',[-0.5,0.5]); % 角度误差
fis = addmf(fis,'input',1,'NB','gaussmf',[0.2,0]); % 负大
fis = addmf(fis,'input',1,'NS','gaussmf',[0.2,0.2]);% 负小
fis = addvar(fis,'input','edot',[ -1,1]); % 角速度误差
fis = addmf(fis,'input',2,'NB','gaussmf',[0.3,0]); % 负大
fis = addmf(fis,'input',2,'NS','gaussmf',[0.3,0.3]);% 负小
% 输出变量定义
fis = addvar(fis,'output','F',[-20,20]); % 控制力
for i=1:4
fis = addmf(fis,'output',1,['K',num2str(i)],'linear',[0,0,0,0]);
end
% 模糊规则库
ruleList = [1 1 1 1 1; % 规则1
1 2 2 1 1; % 规则2
2 1 3 1 1; % 规则3
2 2 4 1 1]; % 规则4
fis = addrule(fis,ruleList);
3. 仿真模型搭建
% 创建Simulink模型
new_system('pendulum_TS_Sim');
open_system('pendulum_TS_Sim');
% 添加模块
add_block('simulink/Sources/Constant','pendulum_TS_Sim/Reference');
add_block('simulink/Math Operations/Sum','pendulum_TS_Sim/Error');
add_block('simulink/Continuous/Transfer Function','pendulum_TS_Sim/Dynamics');
add_block('simulink/Sinks/Scope','pendulum_TS_Sim/Scope');
% 设置TS模糊控制器模块
add_block('fuzzylogic/FIS Controller','pendulum_TS_Sim/Controller');
set_param('pendulum_TS_Sim/Controller','FISFile','pendulum_TS.fis');
% 连接信号线
add_line('pendulum_TS_Sim','Reference/1','Error/1');
add_line('pendulum_TS_Sim','Error/1','Controller/1');
add_line('pendulum_TS_Sim','Controller/1','Dynamics/1');
4. 控制律实现
% 控制量计算(S-Function实现)
function [sys,x0,str,ts] = pendulum_control(t,x,u,flag)
persistent fis
if isempty(fis)
fis = readfis('pendulum_TS.fis');
end
% 模糊推理
e = u(1);
edot = u(2);
output = evalfis([e,edot],fis);
sys = output;
end
三、扩展应用方向
-
多模型融合
% 结合LQR与TS模糊控制 [K,S,e] = lqr(A,B,Q,R); F = -K*x + u_TS; -
硬件在环测试 使用dSPACE实时仿真平台 部署到STM32H743微控制器
-
深度强化学习改进
% DQN策略梯度更新 agent = rlRepresentation(@rlFunctionApproximator,@(x) x,1); trainOpts = rlTrainingOptions('MaxEpisodes',1000); train(agent,env,trainOpts);
参考代码 基于TS模糊模型的倒立摆程序 www.youwenfan.com/contentcnm/79843.html
四、注意事项
-
物理参数匹配 需根据实际系统调整质量、长度等参数
-
采样时间设置 建议采样周期Ts=0.01~0.05秒
-
初始条件设置
x0 = [0.1; 0; 0.05; 0]; % 初始位置偏移0.1m

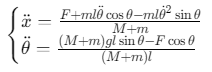

 浙公网安备 33010602011771号
浙公网安备 33010602011771号