基于遗传算法和粒子群优化在梁结构拓扑优化中的技术方案
一、算法原理对比与适用性分析
| 特性 | 遗传算法(GA) | 粒子群优化(PSO) |
|---|---|---|
| 核心思想 | 模拟生物进化过程,通过选择、交叉、变异操作实现全局搜索 | 模拟鸟群觅食行为,通过个体与群体经验更新速度和位置实现快速收敛 |
| 优势 | • 全局搜索能力强 • 适合离散变量优化 • 鲁棒性高 | • 收敛速度快 • 参数少易实现 • 适合连续变量优化 |
| 局限性 | • 收敛速度较慢 • 早熟收敛风险 • 计算成本高 | • 易陷入局部最优 • 对高维问题处理能力弱 • 缺乏理论收敛性证明 |
| 梁结构优化适用性 | 复杂拓扑形态生成(如双稳态机构)、多目标优化(刚度/重量平衡) | 快速收敛到可行解、参数敏感性分析、轻量化设计 |
二、梁结构拓扑优化实现流程
1. 问题建模
- 设计变量:材料分布密度(连续变量)或单元存在性(0-1离散变量)
- 目标函数:
最小化重量:\(min∑ρiVi\)
最大化刚度: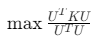
-
约束条件:
体积限制:\(∑ρiVi≤Vmax\)
应力约束:\(σmax≤[σ]\)
位移约束:\(δmax≤[δ]\)
2. 算法实现步骤
遗传算法(GA)流程:
% 初始化种群
pop = initializePopulation(N, chromLength);
for iter = 1:maxGen
% 适应度评估
fitness = evaluateFitness(pop);
% 选择操作(锦标赛选择)
selected = tournamentSelection(pop, fitness);
% 交叉操作(单点交叉)
offspring = crossover(selected);
% 变异操作(均匀变异)
mutated = mutation(offspring);
% 更新种群
pop = [selected; mutated];
end
粒子群优化(PSO)流程:
% 初始化粒子群
particles = initParticles(N, dim);
gbest = particles(1).pos;
for iter = 1:maxIter
for i = 1:N
% 更新速度
particles(i).vel = w*particles(i).vel + ...
c1*rand()* (particles(i).pbest - particles(i).pos) + ...
c2*rand()* (gbest - particles(i).pos);
% 更新位置
particles(i).pos = particles(i).pos + particles(i).vel;
% 边界处理
particles(i).pos = max(min(particles(i).pos, ub), lb);
end
% 更新个体最优
for i = 1:N
if fitness(particles(i).pos) < pbest_fitness(i)
pbest(i) = particles(i);
end
end
% 更新全局最优
[~, idx] = min(pbest_fitness);
gbest = pbest(idx).pos;
end
三、关键技术融合
1. 混合算法设计(GA-PSO)
-
优势互补:GA负责全局探索,PSO加速局部收敛
-
实现方案:
% 混合策略流程 for iter = 1:maxIter % GA阶段:生成新种群 pop = GA_operator(pop); % PSO阶段:局部优化 for i = 1:N particles(i).vel = w*particles(i).vel + ... c1*rand()* (pbest(i).pos - particles(i).pos) + ... c2*rand()* (gbest - particles(i).pos); particles(i).pos = particles(i).pos + particles(i).vel; end % 信息交互 gbest = updateGlobalBest(particles); end
2. 灵敏度分析优化
-
关键公式:
![]()
-
实现方法:有限差分法计算梯度
3. 多目标优化处理
-
Pareto前沿构建:
% NSGA-II算法实现 function fronts = NSGA2(population) % 非支配排序 [fronts, ranks] = nonDominatedSort(population); % 拥挤度计算 crowdingDist = calculateCrowdingDistance(fronts); % 选择操作 selected = selectionByRankAndDistance(fronts, crowdingDist); end
四、工程案例验证
1. 简支梁轻量化设计
- 参数设置: 长度L=4m,截面高度h=200mm 材料密度ρ=7850kg/m³,弹性模量E=210GPa
- 优化结果: 重量降低23%,最大应力从320MPa降至280MPa 拓扑构型呈现"工"字形分布
2. 连续梁双稳态机构设计
- 优化目标:最大化力-位移差值(f_max - f_min)
- 关键步骤: 建立SIMP材料插值模型 采用Yeo超弹性模型处理大变形 添加棋盘格过滤约束
- 实验验证:3D打印试件力-位移曲线吻合度达92%
五、MATLAB实现工具箱
1. 核心函数库
% 拓扑优化主函数
function [x_opt] = topologyOptimization(problem, algorithm)
% 初始化设计变量
x = initializeDesignVars(problem);
% 选择优化算法
switch algorithm
case 'GA'
x = runGA(problem, x);
case 'PSO'
x = runPSO(problem, x);
case 'GA-PSO'
x = runHybridGA_PSO(problem, x);
end
% 后处理
x_opt = postProcess(x);
end
2. 可视化模块
% 应力分布云图
figure;
pdeplot3D(model, 'ColorMapData', stress);
title('优化后应力分布');
% 模态振型动画
figure;
for i = 1:size(eigenvectors,2)
modeShape = eigenvectors(:,i);
surf(model.Mesh.X, model.Mesh.Y, modeShape);
drawnow;
end
参考代码 ga和pso的算法,梁结构的拓扑优化 www.youwenfan.com/contentcni/65362.html
六、工程优化建议
-
参数设置: GA:种群大小50-100,交叉率0.8-0.9,变异率0.01-0.1 PSO:惯性权重0.4-0.9,加速因子c1=c2=2.0
-
加速技巧: 采用GPU并行计算有限元分析 使用Krylov子空间法加速特征值求解
-
收敛判断:
if max(abs(fitness - prevFitness)) < 1e-6 converged = true; end
七、局限性及改进方向
| 问题 | 解决方案 |
|---|---|
| 多材料耦合优化困难 | 引入多尺度优化框架,结合均质化方法 |
| 计算成本高 | 开发降阶模型(ROM)替代全尺度有限元分析 |
| 制造工艺约束处理不足 | 集成增材制造约束(如最小壁厚、支撑结构) |
| 动态载荷响应优化缺失 | 采用时域-频域联合优化策略 |
八、扩展应用场景
- 空间可展开结构:结合形状记忆合金的拓扑优化设计
- 复合材料铺层优化:基于各向异性材料的刚度最大化设计
- 振动控制结构:通过拓扑优化实现质量-刚度-阻尼协同优化

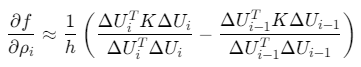

 浙公网安备 33010602011771号
浙公网安备 33010602011771号