最长公共子序列问题（动态规划）

动态规划一般也只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解。

动态规划算法分以下4个步骤：

描述最优解的结构
递归定义最优解的值
按自底向上的方式计算最优解的值   //此3步构成动态规划解的基础。
由计算出的结果构造一个最优解。   //此步如果只要求计算最优解的值时，可省略。

最优子结构

 如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。意思就是，总问题包含很多个子问题，而这些子问题的解也是最优的。

重叠子问题
 子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij=yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。

考虑最长公共子序列问题如何分解成子问题，设A=“a0，a1，…，am-1”，B=“b0，b1，…，bm-1”，并Z=“z0，z1，…，zk-1”为它们的最长公共子序列。不难证明有以下性质：

（1） 如果am-1=bn-1，则zk-1=am-1=bn-1，且“z0，z1，…，zk-2”是“a0，a1，…，am-2”和“b0，b1，…，bn-2”的一个最长公共子序列；

（2） 如果am-1!=bn-1，则若zk-1!=am-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列；

（3） 如果am-1!=bn-1，则若zk-1!=bn-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列。

这样，在找A和B的公共子序列时，如有am-1=bn-1，则进一步解决一个子问题，找“a0，a1，…，am-2”和“b0，b1，…，bm-2”的一个最长公共子序列；如果am-1!=bn-1，则要解决两个子问题，找出“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列和找出“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列，再取两者中较长者作为A和B的最长公共子序列。

求解：

引进一个二维数组c[][]，用c[i][j]记录X[i]与Y[j] 的LCS 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。
我们是自底向上进行递推计算，那么在计算c[i,j]之前，c[i-1][j-1]，c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j]，就可以计算出c[i][j]。

问题的递归式写成：

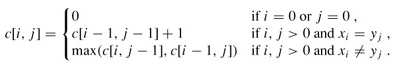
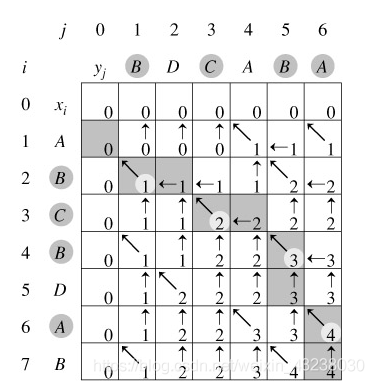
回溯输出最长公共子序列过程：

 

 

package dp;

import java.util.Random;

//使用动态规划找出最长公共子序列
public class LCS {
    public static void main(String[] args) {
        //随机生成指定长度的字符串
        int size = 20;
        String x  = generateRandomStr(size);
        String y  = generateRandomStr(size);

        int m = x.length();
        int n = y.length();
        //创建二维数组，也就是填表的过程
        int[][] c = new int[m+1][n+1];

        //初始化二维数组
        for (int i = 0; i < m+1; i++) {
            c[i][0] = 0;
        }
        for (int i = 0; i < n+1; i++) {
            c[0][i] = 0;
        }

        //实现公式逻辑
        int[][] path = new int[m+1][n+1];//记录通过哪个子问题解决的，也就是递推的路径
        for (int i = 1; i < m+1; i++) {
            for (int j = 1; j < n+1; j++) {
                if(x.charAt(i-1) == y.charAt(j-1)){
                    c[i][j] = c[i-1][j-1] + 1;
                }else if(c[i-1][j] >= c[i][j-1]){
                    c[i][j] = c[i-1][j];
                    path[i][j] = 1;
                }else{
                    c[i][j] = c[i][j-1];
                    path[i][j] = -1;
                }
            }
        }
        //输出查看c
        System.out.println("c:");
        for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                System.out.print(c[i][j]+"\t");
            }
            System.out.println();
        }
        //输出查看path
        System.out.println("path:");
        for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                System.out.print(path[i][j]+"\t");
            }
            System.out.println();
        }

        System.out.printf("%s与%s的最长公共子序列为：\n",x,y);
        PrintLCS(path,x,m,n);


    }

    public static String generateRandomStr(int length) {
        String base = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
        Random random = new Random();
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < length; i++) {
            int number = random.nextInt(base.length());
            sb.append(base.charAt(number));
        }
        return sb.toString();
    }
    public static void PrintLCS(int[][]b,String x,int i,int j){
        if(i == 0 || j == 0){
            return;
        }

        if(b[i][j] == 0){
            PrintLCS(b,x,i-1,j-1);
            System.out.printf("%c",x.charAt(i-1));
        }else if(b[i][j] == 1){
            PrintLCS(b,x,i-1,j);
        }else{
            PrintLCS(b,x,i,j-1);
        }
    }
}

部分引用：https://blog.csdn.net/yysdsyl/article/details/4226630