算法练习（七）：斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

　

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1

　　

示例 2：

输入：n = 5
输出：5

　　

提示：

• 0 <= n <= 100

解题思路：

斐波那契数列的定义是f(n + 1) = f(n) + f(n - 1)，生成第n项的做法有以下几种：

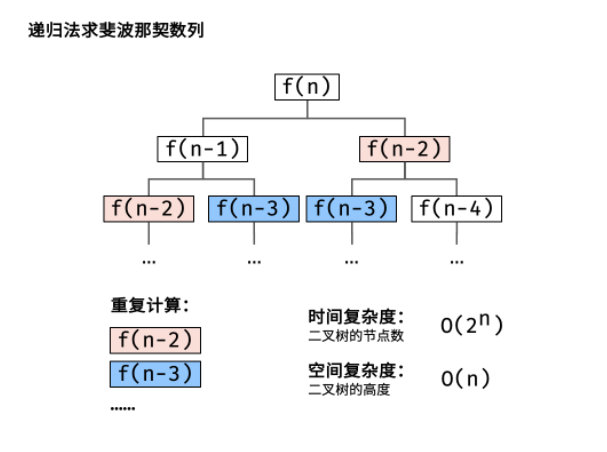
　　1、递归法：

　　　　原理：把f(n)问题的计算拆分成f(n - 1) 和f(n - 2)两个子问题的计算，并递归，以f(0) 和 f(1) 为终止条件。

　　　　缺点：大量重复的递归计算。

 

 　　2、循环求余法：

大数越界： 随着 nn 增大, f(n)f(n) 会超过 Int32 甚至 Int64 的取值范围，导致最终的返回值错误。

• 求余运算规则： 设正整数 x, y,p ，求余符号为 ⊙ ，则有 (x + y) ⊙ p = (x ⊙ p + y ⊙ p) ⊙ p  。
• 解析： 根据以上规则，可推出 f(n) ⊙ p = [f(n-1) ⊙ p + f(n-2) ⊙ p] ⊙ p，从而可以在循环过程中每次计算 sum = (a + b) ⊙ 1000000007，此操作与最终返回前取余等价。

　　复杂度分析：

• 时间复杂度 O(n) ： 计算 f(n) 需循环 n 次，每轮循环内计算操作使用 O(1)。
• 空间复杂度 O(1) ： 几个标志变量使用常数大小的额外空间。

package Algriothm;

public class Fibonacci {

    public static void main(String[] args) {

        System.out.println(fib1(48));
    }

    public static int fib(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        return fib(n - 1) + fib(n - 2);
    }

    public static int fib1(int n) {
        int a = 0, b = 1, sum;
        for (int i = 0; i < n; i++) {
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
        }
        return a;
    }
}