Python小白的数学建模课-B2. 新冠疫情 SI模型


传染病的数学模型是数学建模中的典型问题，常见的传染病模型有 SI、SIR、SIRS、SEIR 模型。

SI 模型是最简单的传染病模型，适用于只有易感者和患病者两类人群。

我们就从 SI 模型开始吧，从模型、例程、运行结果到模型分析，全都在这个系列中。

『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。

Python小白的数学建模课-09.微分方程模型
Python小白的数学建模课-B2.新冠疫情 SI模型
Python小白的数学建模课-B3.新冠疫情 SIS模型
Python小白的数学建模课-B4.新冠疫情 SIR模型
Python小白的数学建模课-B5.新冠疫情 SEIR模型
Python小白的数学建模课-B6.改进 SEIR疫情模型


1. 前言

新冠疫情不仅严重影响到全球的政治和经济，深刻和全面地影响着社会和生活的方方面面，也已经成为数学建模竞赛的背景帝。

传染病的数学模型是数学建模中的典型问题，标准名称是流行病的数学模型（Mathematical models of epidemic diseases）。建立传染病的数学模型来描述传染病的传播过程，研究传染病的传播速度、空间范围、传播途径、动力学机理等问题，以指导对传染病的有效地预防和控制，具有重要的现实意义。

不同类型传染病的传播具有不同的特点，传染病的传播模型不是从医学角度分析传染病的传播过程，而是按照传播机理建立不同的数学模型。

首先，把传染病流行范围内的人群分为 S、E、I、R 四类，具体含义如下：

  • S 类（Susceptible），易感者，指缺乏免疫能力的健康人，与感染者接触后容易受到感染；

  • E 类（Exposed），暴露者，指接触过感染者但暂无传染性的人，适用于存在潜伏期的传染病；

  • I 类（Infectious），患病者，指具有传染性的患病者，可以传播给 S 类成员将其变为 E 类或 I 类成员；

  • R 类（Recovered），康复者，指病愈后具有免疫力的人。如果免疫期有限，仍可以重新变为 S 类成员，进而被感染；如果是终身免疫，则不能再变为 S类、E类或 I 类成员。

常见的传染病模型按照传染病类型分为 SI、SIR、SIRS、SEIR 模型等，就是由以上四类人群根据不同传染病的特征进行组合而产生的不同模型。


------

2. 疫情传播 SI 模型

2.1 SI 模型的适用范围

SI 模型适用于只有易感者和患病者两类人群，且无法治愈的疾病，例如 T型病、僵尸。

2.2 SI 模型的假设

  1. 考察地区的总人数 N 不变，即不考虑生死或迁移；
  2. 人群分为易感者（S类）和患病者（I类）两类；
  3. 易感者（S类）与患病者（I类）有效接触即被感染，变为患病者，无潜伏期、无治愈情况、无免疫力；
  4. 每个患病者每天有效接触的易感者的平均人数（日接触数）是 \(\lambda\)，称为日接触率；
  5. 将第 t 天时 S类、I 类人群的占比记为 \(s(t)\)、\(i(t)\)，数量为 \(S(t)\)、\(I(t)\)；初始日期 \(t=0\) 时， S类、I 类人群占比的初值为 \(s_0\)、\(i_0\)。

2.3 SI 模型的微分方程

由

\[\begin{align*} N\frac{di}{dt} = N\lambda s i \end{align*} \]

得：

\[\begin{align*} \frac{di}{dt} = \lambda i (1-i)，\ i(0) = i_0 \end{align*} \]

这是 Logistic 模型，用分离变量法可以求出其解析解为：

\[\begin{align*} & i(t)=\frac{1}{1+(1/i_0 - 1)\ e^{-\lambda t}}\\ & I(t)= N\ i(t) \end{align*} \]


3. SI 模型的 Python 编程

3.1 SI 模型的解析解

上文已经得到 SI 模型的解析解，对此很容易通过 Python 编程实现，详见本文例程。

虽然 SI 模型的解析解并不复杂，而且解的精度当然是最好的，但我们仍然不鼓励用解析解的方法。原因在于，一是对于小白求解析解的过程相对复杂困难，而且可能出错，二是对于更复杂的模型是没有解析解的，即便大神也只能用数值方法求解。既然如此，不如从一开始就学习、掌握数值求解方法，熟悉数值解法的编程实现。

3.2 SI 模型的数值解

SI 模型是常微分方程初值问题，可以使用 Scipy 工具包的 scipy.integrate.odeint() 函数求数值解，具体方法可以参考前文《Python小白的数学建模课-09 微分方程模型》。

scipy.integrate.odeint(func, y0, t, args=())

**scipy.integrate.odeint() **是求解微分方程的具体方法，通过数值积分来求解常微分方程组。

odeint() 的主要参数：

  • func: callable(y, t, …) 　　导数函数 \(f(y,t)\) ，即 y 在 t 处的导数，以函数的形式表示
  • y0: array：　　初始条件 \(y_0\)，对于常微分方程组 \(y_0\) 则为数组向量
  • t: array：　　求解函数值对应的时间点的序列。序列的第一个元素是与初始条件 \(y_0\) 对应的初始时间 \(t_0\)；时间序列必须是单调递增或单调递减的，允许重复值。
  • args: 向导数函数 func 传递参数。当导数函数 \(f(y,t,p1,p2,..)\) 包括可变参数 p1,p2.. 时，通过 args =(p1,p2,..) 可以将参数p1,p2.. 传递给导数函数 func。

odeint() 的返回值：

  • y: array 　　数组，形状为 (len(t),len(y0)，给出时间序列 t 中每个时刻的 y 值。

odeint() 的编程步骤：

  1. 导入 scipy、numpy、matplotlib 包；
  2. 定义导数函数 \(f(i,t)=\lambda i (1-i)\) ；
  3. 定义初值 \(i_0\) 和 \(i\) 的定义区间 \([t_0,\ t]\)；
  4. 调用 odeint() 求 \(i\) 在定义区间 \([t_0,\ t]\) 的数值解。

3.3 Python例程：SI 模型的解析解与数值解

# 1. SI 模型，常微分非常，解析解与数值解的比较
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np  # 导入 numpy包
import matplotlib.pyplot as plt  # 导入 matplotlib包

def dy_dt(y, t, lamda, mu):  # 定义导数函数 f(y,t)
    dy_dt = lamda*y*(1-y)  # di/dt = lamda*i*(1-i)
    return dy_dt

# 设置模型参数
number = 1e7  # 总人数
lamda = 1.0  # 日接触率, 患病者每天有效接触的易感者的平均人数
mu1 = 0.5  # 日治愈率, 每天被治愈的患病者人数占患病者总数的比例
y0 = i0 = 1e-6  # 患病者比例的初值
tEnd = 50  # 预测日期长度
t = np.arange(0.0,tEnd,1)  # (start,stop,step)

yAnaly = 1/(1+(1/i0-1)*np.exp(-lamda*t))  # 微分方程的解析解
yInteg = odeint(dy_dt, y0, t, args=(lamda,mu1))  # 求解微分方程初值问题
yDeriv = lamda * yInteg *(1-yInteg)

# 绘图
plt.plot(t, yAnaly, '-ob', label='analytic')
plt.plot(t, yInteg, ':.r', label='numerical')
plt.plot(t, yDeriv, '-g', label='dy_dt')
plt.title("Comparison between analytic and numerical solutions")
plt.legend(loc='right')
plt.axis([0, 50, -0.1, 1.1])
plt.show()

3.4 解析解与数值解的比较

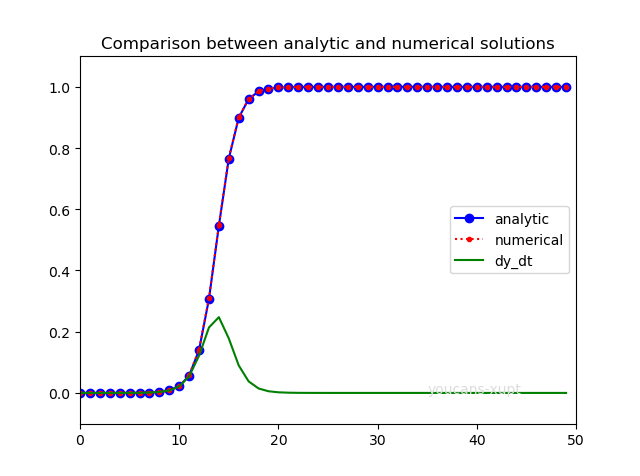
本图为例程 2.3 的运行结果，图中对解析解（蓝色）与使用 odeint() 得到的数值解（红色）进行比较。在该例中，无法观察到解析解与数值解的差异，表明数值解的误差很小。

图中 \(di/dt\) 具有最大值，最大值表示疫情增长的高潮，达到最大值后 \(di/dt\) 逐渐减小，但患病者比例很快增长到 100%，表明所有人都被感染成为患者。

这是特定参数的结果，还是模型的必然趋势，需要对参数的影响进行更详细的研究。


4. SI 模型参数的影响

对于 SI 模型，只有日接触率 \(\lambda\) 和患病者比例的初值 \(i_0\) 会影响模型的结果，其它参数如总人数 N 并没有影响。

4.1 日接触率对 SI 模型的影响

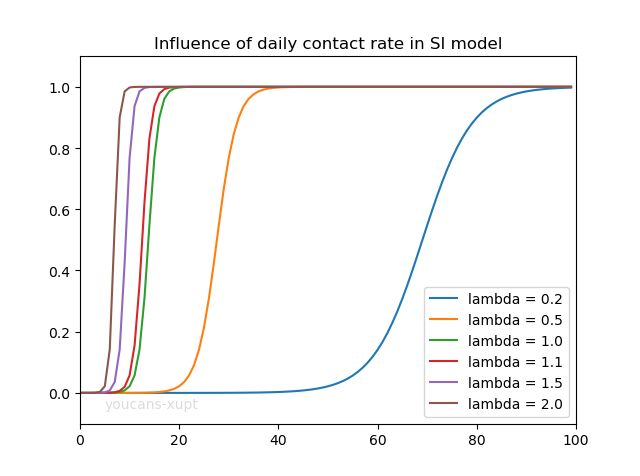
对不同日接触率的比较表明：

  1. 日接触率越大，疫情从发生到爆发的时间越短，爆发过程的增长速度也越快。
  2. 不论日接触率多大，患病者的比例最终都会增长到 1，表明所有人都被感染成为患者。
  3. 不论日接触率多大，都具有缓慢发展、爆发、增长放缓 3 个阶段，进入爆发阶段后患病者的比例急剧增长，疫情就很难控制了。

4.2 患病者比例的初值对 SI 模型的影响

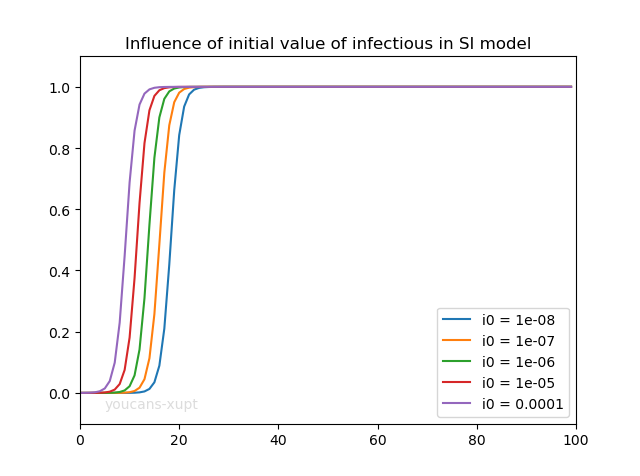
对患病者比例初值的比较表明，患病者初值的人数或比例只影响疫情爆发期到来的快慢，对疫情传播的过程和结果几乎没有影响。

这与我们直观的经验不太一致，一个原因是 SI 模型本身存在不足，另一方面也说明如果对传染病不加控制，即使开始患病人数很少，经过一段时间的传播后也终将会引起爆发。

4.3 SI 模型结果讨论

  1. 在 \(i(t)=0.5,\ I(t) = N/2\) 时 $ di/dt$ 达到最大值，病人数目 \(I(t)\) 增加最快。由此可以预报传染病高潮的到来，即为医院的门诊量最大的一天，卫生部门要重点关注。
  2. \(t_m\) 与 \(\lambda\) 成反比。日接触率 \(\lambda\) 反映卫生水平、防控手段，提高卫生水平、强化防控手段，降低病人的日接触率，可以推迟传染病高潮的到来。
  3. 当 $ t \to \infty$ 时 \(i \to 1\) ，表明所有人最终都会被传染而变成病人。这完全不符合实际情况，表明该模型太不讲 politics 了，只能适用于美帝国家建模。
  4. SI 模型非常明显而严重的缺陷，是该模型没有考虑患病者可以治愈，因此只能是健康人患病，而患病者不能恢复健康（甚至也不会死亡，而是不断传播疫情），所以终将全部被传染。

【本节完】

版权声明：

欢迎关注『Python小白的数学建模课 @ Youcans』 原创作品

原创作品，转载必须标注原文链接：(https://www.cnblogs.com/youcans/p/14944259.html)。

Copyright 2021 Youcans, XUPT

Crated：2021-06-09


欢迎关注 『Python小白的数学建模课 @ Youcans』，每周更新数模笔记
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型
Python小白的数学建模课-B2.新冠疫情 SI模型
Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法


posted @ 2021-06-28 14:09  youcans  阅读(3311)  评论(1)  编辑  收藏  举报