CYCADA: cycle-consistent adversaial domain adaption阅读笔记

CYCADA: cycle-consistent adversaial domain adaption阅读笔记

目录

• CYCADA: cycle-consistent adversaial domain adaption阅读笔记
  • 作者的方法
    • adversarial objective
    • cycle consistency
    • semantic consistency
    • feature level

之前方法是在feature space进行domain adaption，来发现domain invariant representations, 但是这种方法很难可视化，而且某些时候不能够获取pixel-level和low-level domain shift. 最近的gan在使用cycle一致性约束的GAN在不同的domain上进行图片mapping取得了很好的效果，即使没有使用aligned image pairs.

作者这篇文章提出了一种新的通过判别方式训练的Cycle-Consistent Adversarial Domain Adaption model. CYCADA能够在pixel-level和feature level上同时adapt，通过添加cycle-consistency约束的同时，还会使用task相关的loss，并且不需要对其的pairs。作者的这种settting可以用到很多不同的任务。达到了比较好的效果。

作者的方法

假设source data为 \(X_S\), source label为\(Y_S\), target data为\(X_T\), 但是没有target label，UDA的目标是学习一个模型\(f\)使得能够准确地预测出来target data \(X_T\).

因为source data上有label，所以source model \(f_S\)在source data上可以学到。对应的就是\(K\)个类别的使用二值交叉熵分类问题：

\[\mathcal{L}_{\text {task }}\left(f_{S}, X_{S}, Y_{S}\right)=-\mathbb{E}_{\left(x_{s}, y_{s}\right) \sim\left(X_{S}, Y_{S}\right)} \sum_{k=1}^{K} \mathbb{1}_{\left[k=y_{s}\right]} \log \left(\sigma\left(f_{S}^{(k)}\left(x_{s}\right)\right)\right) \]

\(\sigma\)表示softmax函数。但是在source domain熵表现很好的\(f_S\)，因为domain shift，在targetdomain会掉点。为了缓解这种domain shift, 作者follow之前的对抗适应方式，通过学习在domain之间map samples，这样的话，一个adversaial discriminator就不能够区分来自于哪个domain。通过mapping samples到一个common space，作者说能够让模型在source domain上进行学习，还能够泛化到target data上。

adversarial objective

基于此，作者提出了一个generator，来mapping from source to target \(G_{S \rightarrow T}\). 通过训练\(G_{S \rightarrow T}\)来产生target data，以及foll adversarial discriminator \(D_T\). 反过来，adversaial discriminator尝试将real target data从source target data充区分出来，对应的loss函数为

\[\mathcal{L}_{\mathrm{GAN}}\left(G_{S \rightarrow T}, D_{T}, X_{T}, X_{S}\right)=\mathbb{E}_{x_{t} \sim X_{T}}\left[\log D_{T}\left(x_{t}\right)\right]+\mathbb{E}_{x_{s} \sim X_{S}}\left[\log \left(1-D_{T}\left(G_{S \rightarrow T}\left(x_{s}\right)\right)\right)\right] \]

上面这个公式的意义是，给定source data，能够确保\(G_{S \rightarrow T}\)产生convincing target samples。相应的，这种能够在不同domain map samples的能力能够让我们通过优化函数\(\mathcal{L}_{\text {task }}\left(f_{T}, G_{S \rightarrow T}\left(X_{S}\right), Y_{S}\right)\)学习到一个target model \(f_T\)，对应下图的绿色部分

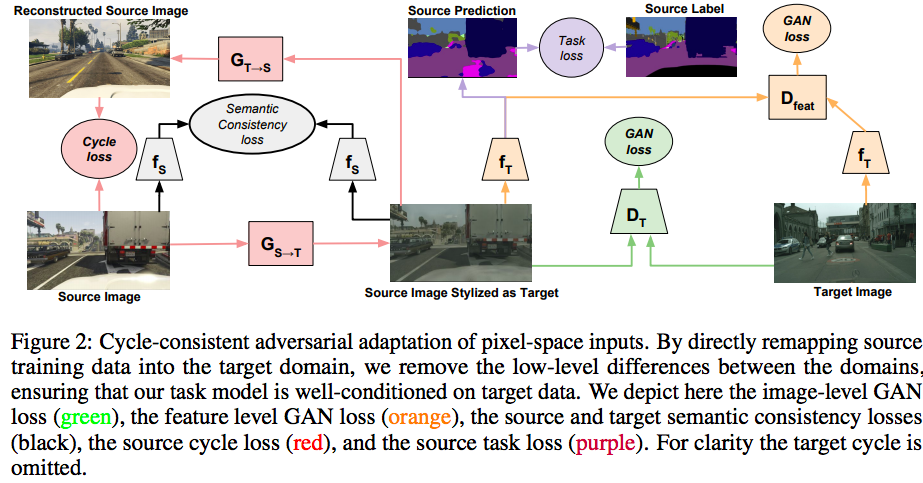
cycle consistency

作者说上述这种方式训练的时候不稳定，而且容易失败。作者的原话如下

Although the GAN loss in Equation 2 ensures that \(G_{S \rightarrow T}\) for some xs will resemble data drawn from \(X_T\), there is no way to guarantee that \(G_{S \rightarrow T}\) preserves the structure or content of the original sample \(x_s\)

为了能够保证或者是encourage source content在conversion的过程中能够保留，作者在他们的adaption method添加了cycle-consistency的约束。如上图中的红色部分。同时作者也提出了利用another mapping from target to source \(G_{T \rightarrow S}\),也是利用GAN loss \(\mathcal{L}_{\mathrm{GAN}}\left(G_{T \rightarrow S}, D_{S}, X_{S}, X_{T}\right)\) 来训练

作者要求的是，从source 到target 然后再从合成的target 到source应该是要和source一致的，所以有个约束是：

\[G_{T \rightarrow S}\left(G_{S \rightarrow T}\left(x_{s}\right)\right) \approx x_{s} \]

以及

\[G_{S \rightarrow T}\left(G_{T \rightarrow S}\left(x_{t}\right)\right) \approx x_{t} \]

作者使用\(\mathcal{L}_1\) norm来进行约束，定义如下cycle consistency loss

\[\begin{aligned} \mathcal{L}_{\text {cyc }}\left(G_{S \rightarrow T}, G_{T \rightarrow S}, X_{S}, X_{T}\right) &=\mathbb{E}_{x_{s} \sim X_{S}}\left[\left\|G_{T \rightarrow S}\left(G_{S \rightarrow T}\left(x_{s}\right)\right)-x_{s}\right\|_{1}\right] \\ &+\mathbb{E}_{x_{t} \sim X_{T}}\left[\left\|G_{S \rightarrow T}\left(G_{T \rightarrow S}\left(x_{t}\right)\right)-x_{t}\right\|_{1}\right] \end{aligned} \]

semantic consistency

同时，作者说他们能够接触到source labeled data，在image translation前后，作者显式的保留高的语义一致性。

作者通过一个预训练的网络\(f_S\)，固定这个网络的权重，用这个模型作为一个noisy labeler。作者希望的是，在translation前后，都希望对于迁移的像素能够用一个fixed classifier \(f\) 进行中正确的分类,给定一个输入\(X\)， 用classifer \(f\)进行分类之后得到的输出为

\[p(f, X)=\arg \max (f(X)) \]

于是，作者定义了一个在图像translation前后的语义一致性的loss：

\[\begin{aligned} \mathcal{L}_{\mathrm{sem}}\left(G_{S \rightarrow T}, G_{T \rightarrow S}, X_{S}, X_{T}, f_{S}\right) &=\mathcal{L}_{\mathrm{task}}\left(f_{S}, G_{T \rightarrow S}\left(X_{T}\right), p\left(f_{S}, X_{T}\right)\right) \\ &+\mathcal{L}_{\mathrm{task}}\left(f_{S}, G_{S \rightarrow T}\left(X_{S}\right), p\left(f_{S}, X_{S}\right)\right) \end{aligned} \]

上图中的 黑色部分。

feature level

通过上述三种方式，作者引入了cycle consistency， semantic consistency，以及adversarial objectives来得到最终的target model。作为一个pixel-level method，adversarial项包含了一个判别器，这个判别器能够区分两种图像，比如从source迁移过来的或者是真实的target。自然而然的可以考虑在feature level进行判别，即一个feature 来自于从soruce domain生成的或者是real target的feature，如上襦的 橘色部分。feature level上的loss定义如下

\[\mathcal{L}_{\mathrm{GAN}}\left(f_{T}, D_{\mathrm{feat}}, f_{S}\left(G_{S \rightarrow T}\left(X_{S}\right)\right), X_{T}\right) \]

所以总共的loss如下：

\[\begin{aligned} \mathcal{L}_{\text {CyCADA }} &\left(f_{T}, X_{S}, X_{T}, Y_{S}, G_{S \rightarrow T}, G_{T \rightarrow S}, D_{S}, D_{T}\right) \\ &=\mathcal{L}_{\text {task }}\left(f_{T}, G_{S \rightarrow T}\left(X_{S}\right), Y_{S}\right) \\ &+\mathcal{L}_{\text {GAN }}\left(G_{S \rightarrow T}, D_{T}, X_{T}, X_{S}\right)+\mathcal{L}_{\text {GAN }}\left(G_{T \rightarrow S}, D_{S}, X_{S}, X_{T}\right) \\ &+\mathcal{L}_{\text {GAN }}\left(f_{T}, D_{\text {feat }}, f_{S}\left(G_{S \rightarrow T}\left(X_{S}\right)\right), X_{T}\right) \\ &+\mathcal{L}_{\text {cyc }}\left(G_{S \rightarrow T}, G_{T \rightarrow S}, X_{S}, X_{T}\right)+\mathcal{L}_{\text {sem }}\left(G_{S \rightarrow T}, G_{T \rightarrow S}, X_{S}, X_{T}, f_{S}\right) \end{aligned} \]

最后的优化目标变成：

\[f_{T}^{*}=\underset{f_{T}}{\arg \min } \min _{G_{S \rightarrow T} \atop G_{T \rightarrow S}} \max _{D_{S}, D_{T}} \mathcal{L}_{\mathrm{CyCADA}}\left(f_{T}, X_{S}, X_{T}, Y_{S}, G_{S \rightarrow T}, G_{T \rightarrow S}, D_{S}, D_{T}\right) \]