Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization论文阅读笔记

Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization论文阅读笔记

目录

• Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization论文阅读笔记
  • background
    • BN
    • IN
    • CIN
  • AdaIN
  • 训练

这篇文章是基于gatys et al这篇做的，gatys et al他们通过在一张content image上引入另外一张图片的style，但是他们的方法是迭代式优化，实际中非常有应用限制。当然也有一些工作做了fast approximation，但是这种方法只能与一种style进行绑定，所以非常有应用限制。这篇文章，作者提出了一个simple yet effective approach, 能够transfer 任意的style in real-time. 作者方法的核心是一个novel adaptive instance normalization (AdaIN) layer，这个层能够对齐content image feature的mean和variance到style image feature 的mean和variance。作者说他们的方法和现在的sota方法速度接近，而不只受限于一种style。除此之外，作者说他们的方法能够让用户flexible control such as content-style trade-off.

作者说他的工作的灵感来自于instance nomalization (IN) layer,这个层在feed forward style transfer非常的effective，作者提出了一种新的解释是，IN 实际上是做的通过normalizing feature statistics 来做style normalization, 这个过程是带有style information的。得益于这种解释，作者提出了simple extension to IN, namely adaptive instance nomalization (AdaIN).具体做的过程是

给定一个content input和style input， AdaIN 通过调整content的mean和variance来match style 的input的mean和variance。

通过实验，作者发现AdaIN能够有效的combines the content of the former and the style of latter by transferring feature statistics.

然后学习一个decoder network，通过inverting the AdaIN output back to the image来产生最终的stylized image，

background

作者先回顾了一下几种normalization，然后通过实验阐明了IN实际上是style transfer的效果

BN

BN学习得到的参数\(\gamma\) 和\(\beta\)，过程如下所示：

\[\mathrm{BN}(x)=\gamma\left(\frac{x-\mu(x)}{\sigma(x)}\right)+\beta \]

其中\(\gamma, \beta \in \mathbb{R}^{C}\),一共有\(C\)个参数，\(\mu(x), \sigma(x) \in \mathbb{R}^{C}\)表示对于每个通道求得的均值和方差，对于每一个channel而言，求取方式如下

\[\mu_{c}(x)=\frac{1}{N H W} \sum_{n=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W} x_{n c h w} \]

\[\sigma_{c}(x)=\sqrt{\frac{1}{N H W} \sum_{n=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W}\left(x_{n c h w}-\mu_{c}(x)\right)^{2}+\epsilon} \]

BN在训练过程汇总，使用的是一个mini-batch中的统计，在inference阶段使用的是popular statistics。

IN

作者先引用了两个文献，一篇最开始做feed-forward的style transfer的文章，使用的是BN，然后文献52简单的将BN替换为IN，然后可以极大的改善效果，IN layer可以由如下公式描述：

\[\mathrm{IN}(x)=\gamma\left(\frac{x-\mu(x)}{\sigma(x)}\right)+\beta \]

和BN不一样的是，这里的\(\mu(x)\)和\(\sigma(x)\)对每一个sample都在spatial dimension单独做，可以由如下公式描述

\[\mu_{n c}(x)=\frac{1}{H W} \sum_{h=1}^{H} \sum_{w=1}^{W} x_{n c h w} \]

\[\sigma_{n c}(x)=\sqrt{\frac{1}{H W} \sum_{h=1}^{H} \sum_{w=1}^{W}\left(x_{n c h w}-\mu_{n c}(x)\right)^{2}+\epsilon} \]

CIN

conditional instance normalization是分组学习，learns a different set of parameters \(\gamma^s\) and \(\beta^s\) for each style \(s\)：

\[\operatorname{CIN}(x ; s)=\gamma^{s}\left(\frac{x-\mu(x)}{\sigma(x)}\right)+\beta^{s} \]

在训练阶段，一个style image together with its index \(s\) are randomly chosen from a fixed set of styles \(s\in \left\{1,2,...,S\right\}\)。然后使用style transfer network， 以及该style 对应的\(\gamma^s\) 和\(\beta^s\)。完成训练过程之后，网络可以使用在IN中不同的affine parameters产生不同风格的图片（网络的其他部分是一样的）。

然后作者通过实验验证了IN中的addine实际上是某种style。如果IN中的一组affine代表一组style，那对于任意的style通过改变affine是否都可以迁移？

AdaIN

然后作者通过对齐content input \(x\) 和style input \(y\)的mean 和variance，不像BN, IN, 或者是CIN，AdaIN没有可学习的affine parameters。相反的，AdaIN不断的从style input计算affine parameters。如下所示：

\[\operatorname{AdaIN}(x, y)=\sigma(y)\left(\frac{x-\mu(x)}{\sigma(x)}\right)+\mu(y) \]

作者说他们简单的scale the normalized content input with \(\sigma(y)\)， shift it with \(\mu(y)\)。和IN相似的是，这些参数are computed across spatial locations.

作者提出的网络如下所示：

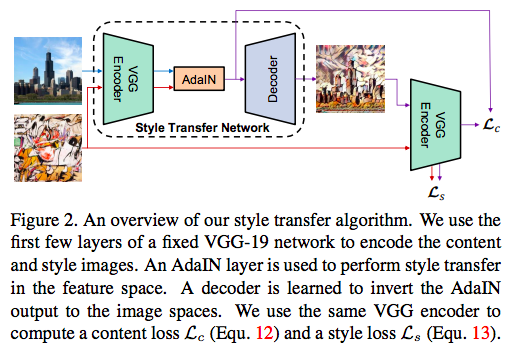
作者的style transfer network \(T\) takes a content image \(c\) 和arbitrary style image \(s\) as input,然后合成output image，保留content image的内容，同时拥有style的风格。

作者才用了一个simplt的encoder-decoder的结果，encoder \(f\) 的前几层是固定的权重，这个encoder对于content 和style image进行encoding之后，作者将这两个feature 输送到adain，来对齐content到style的mean 和variance，来得到target feature map \(t\):

\[t=\operatorname{AdaIN}(f(c), f(s)) \]

然后一个随机初始化的decoder \(g\) is trained to map \(t\) back to the image space, generating the stylized image \(T(c, s)\)

\[T(c, s)=g(t) \]

decoder和encoder基本上是对称关系，decoder中没有用BN或者IN，因为作者说了IN只能迁移到一种style

训练

作者使用了两种loss，一种是content loss，还有一种是style loss

content是迁移之后的图片，再输入到vgg中，和原始的feature \(t\)的距离；定义如下

\[\mathcal{L}_{c}=\|f(g(t))-t\|_{2} \]

因为作者说他们的AdaIN layer只transfer the mean and standard deviation of the style features，作者的style loss只能够match 这些统计量，定义如下

\[\begin{array}{r} \mathcal{L}_{s}=\sum_{i=1}^{L}\left\|\mu\left(\phi_{i}(g(t))\right)-\mu\left(\phi_{i}(s)\right)\right\|_{2}+ \\ \sum_{i=1}^{L}\left\|\sigma\left(\phi_{i}(g(t))\right)-\sigma\left(\phi_{i}(s)\right)\right\|_{2} \end{array} \]

\(\phi_i\)表示vgg-19中的layer