Q-Learning，DQN

1 概念

 

 

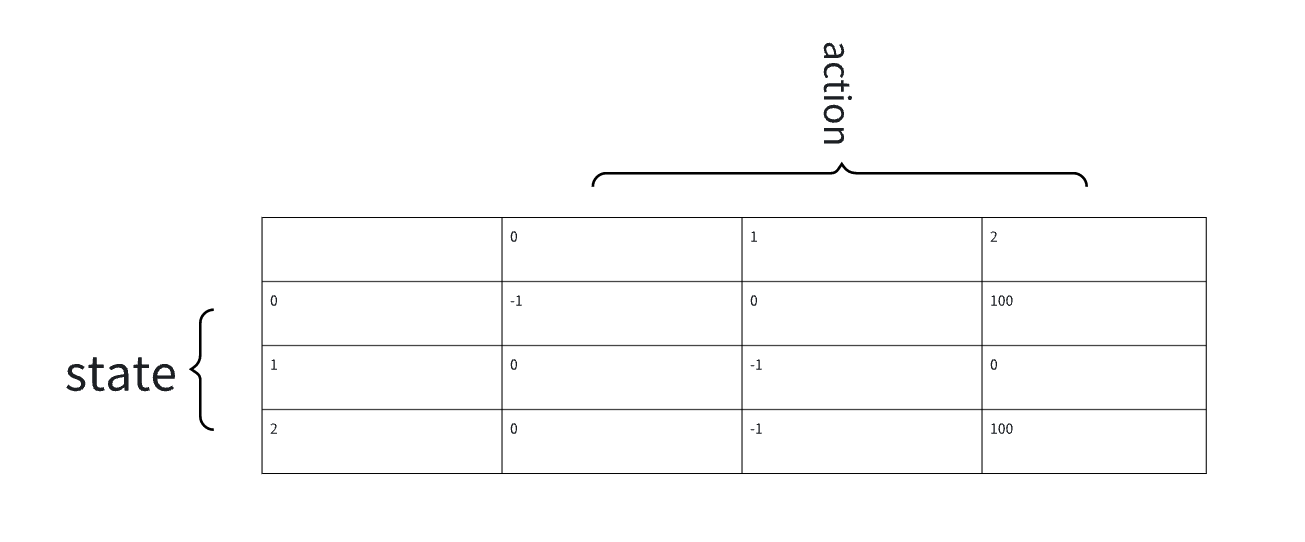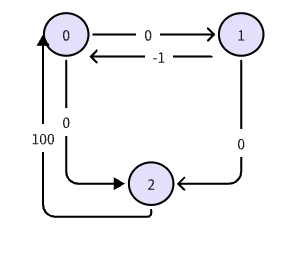
• state 状态
• action 行动
• reward function 奖励
• policy 策略
• discount rate 衡量当前奖励与未来奖励

 

2、 Q 与 V

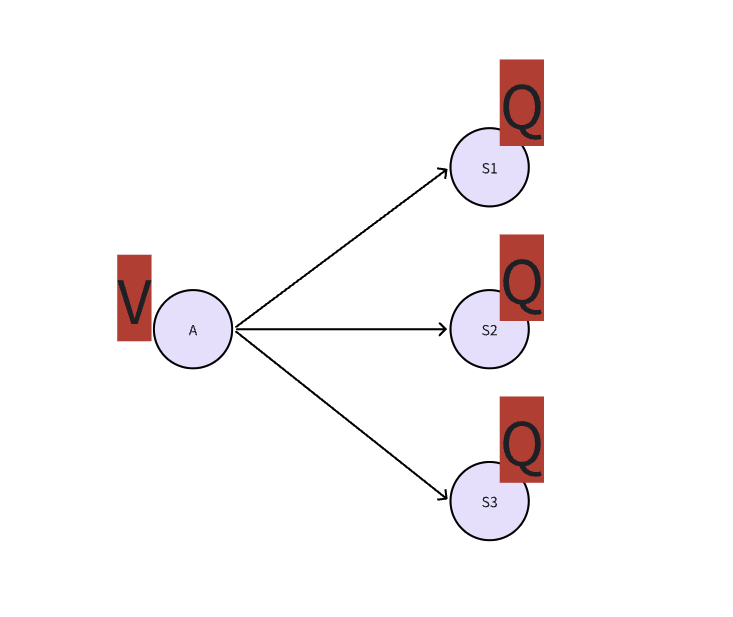
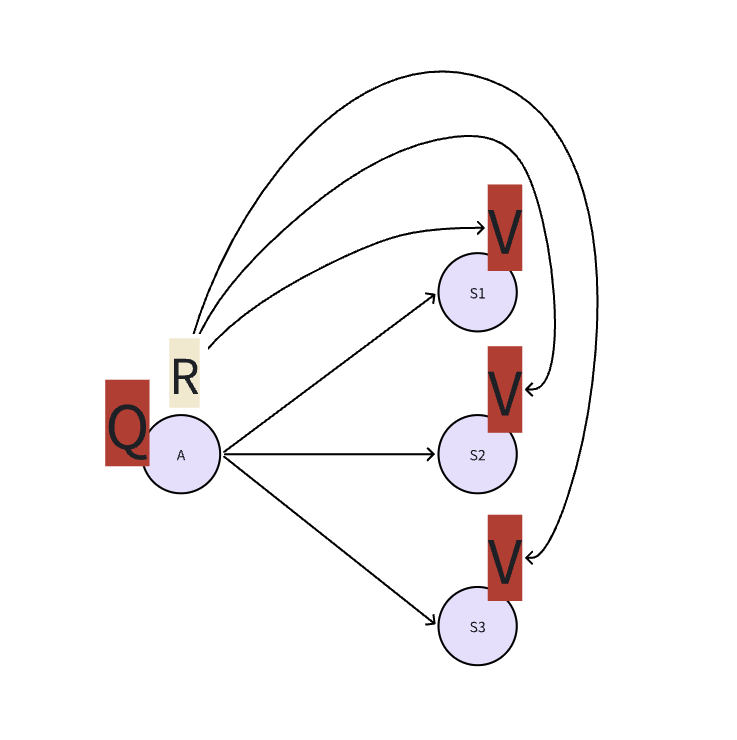
• 动作的价值 Q：代表智能体选择这个动作A后，一直到最终状态奖励总和的期望。告诉你在这个状态下执行某个具体动作有多好。Q，告诉你在S状态下，应该做什么动作
• 评估状态的值V，它代表了智能体在这个状态S下，一直到最终状态的奖励总和的期望。告诉你这个state好不好

一个状态的V值，就是这个状态下所有动作的Q值，在策略下的期望。

$$\displaystyle{\displaylines{V_{\pi}(S)=\sum_{A}^{}\pi(A|S)Q_{\pi}(S,A)}}$$

 

 

从V到Q当我们选择A并转移状态的时候会获得一个奖励Reward，因此要把这个R也算上。则公式如下：

 

 

$$\displaystyle{\displaylines{Q_{\pi}(S,A)=R_{s}^{a}+\gamma\sum_{s}^{}P_{Ss}^{a}V_{\pi}(s)}}$$

 

• P是状态转移概率
• π是一个state到动作action的映射。行为策略通常是概率分布（收集经验），目标策略确定性的（贪心），最终策略确定的（argmax Q）

 

3 Q值更新

Q(s,a) = Q(s,a) + α [R + γ·max_{a'} Q(s',a') - Q(s,a)]

• α 为学习率
• γ 折扣因子
• R 即时奖励
• s' 新状态max_{a'} Q(s',a')：下一个状态的最大Q值

这个公式就是用 ‘实际获得的奖励加上对未来奖励的估计’和‘当前的Q值’之间的差距，来更新Q值

伪代码

# Q-learning伪代码
初始化 Q-table（全零或随机小值）
设置参数 α, γ, ε

for episode in range(num_episodes):
    s = 初始状态
    while s不是终止状态:
        # 1. 选择动作（ε-greedy）
        if random() < ε:
            a = 随机动作  # 探索
        else:
            a = argmax_a Q(s,a)  # 利用
        
        # 2. 执行动作，观察结果
        执行动作a，获得奖励R和新状态s'
        
        # 3. Q值更新
        TD_target = R + γ * max_{a'} Q(s',a')
        TD_error = TD_target - Q(s,a)
        Q(s,a) = Q(s,a) + α * TD_error
        
        # 4. 转移到新状态
        s = s'

 

通过贝尔曼更新传播到更早的状态，类似于反向传播，例子

import numpy as np

np.random.seed(42)
Q = np.zeros(4)  # 状态A,B,C,D的Q值（假设每个状态只有一个动作）
alpha, gamma = 0.5, 0.9
reward_D = 10  # 到达D的奖励

print("=== 第一轮探索 ===")
Q[2] = Q[2] + alpha * (reward_D + gamma * Q[3] - Q[2])
print(f"更新Q(C) = {Q[2]:.2f} (用Q(D)={Q[3]:.2f})")
Q[1] = Q[1] + alpha * (-1 + gamma * Q[2] - Q[1])
print(f"更新Q(B) = {Q[1]:.2f} (用Q(C)={Q[2]:.2f})")
Q[0] = Q[0] + alpha * (-1 + gamma * Q[1] - Q[0])
print(f"更新Q(A) = {Q[0]:.2f} (用Q(B)={Q[1]:.2f})")
print(f"\n第一轮后: Q = {Q}")

print("\n=== 第二轮探索 ===")
old_Q_C = Q[2]
Q[2] = Q[2] + alpha * (reward_D + gamma * Q[3] - Q[2])
print(f"更新Q(C): {old_Q_C:.2f} → {Q[2]:.2f}")
old_Q_B = Q[1]
Q[1] = Q[1] + alpha * (-1 + gamma * Q[2] - Q[1])
print(f"更新Q(B): {old_Q_B:.2f} → {Q[1]:.2f} (用更好的Q(C))")
old_Q_A = Q[0]
Q[0] = Q[0] + alpha * (-1 + gamma * Q[1] - Q[0])
print(f"更新Q(A): {old_Q_A:.2f} → {Q[0]:.2f} (用稍好的Q(B))")

输出

=== 第一轮探索 ===
更新Q(C) = 5.00 (用Q(D)=0.00)
更新Q(B) = 1.75 (用Q(C)=5.00)
更新Q(A) = 0.29 (用Q(B)=1.75)

第一轮后: Q = [0.2875 1.75   5.     0.    ]

=== 第二轮探索 ===
更新Q(C): 5.00 → 7.50
更新Q(B): 1.75 → 3.75 (用更好的Q(C))
更新Q(A): 0.29 → 1.33 (用稍好的Q(B))

异策略：主要目的是从非最优行为中学习最优策略，探索只是其行为策略的一部分特性。

 

4、DQN

如果状态空间和动作空间比较小，我们可以用Q表来存储，但是如果状态空间很大，用表格存储状体就不现实了。DQN引入了深度神经网络来近似Q值。输入是状态s，输出是每个动作对应的Q值。

4.1 经验回放机制

在训练过程中，智能体与环境交互产生很多的经验，这些经验可以表示为四元组 (s, a, r, s')，分别是状态、动作、奖励和下一个状态。传统的Q学习是直接用每次获得的经验来更新Q值，但这样会存在一些问题，比如前后经验可能存在很强的相关性，导致学习不稳定。而经验回放是把这些经验存储到一个经验回放池中，然后在训练神经网络的时候，从经验回放池中随机采取一批来更新网络参数。这么做的优点

• 打破了经验之间的相关性
• 同样的经验可以被多次使用
• 早起训练 e 很高，大力探索，收集多样的经验，然后随时间衰减到一个比较小的值

 

代码

class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)  # 固定大小的队列
        
    def add(self, experience):
        # 添加新经验，如果缓冲区已满，自动移除最旧的经验
        self.buffer.append(experience)
    
    def sample(self, batch_size):
        # 随机采样一批经验
        indices = np.random.choice(len(self.buffer), batch_size, replace=False)
        batch = [self.buffer[i] for i in indices]
        
        # 将批次数据转换为适合训练的格式
        states, actions, rewards, next_states, dones = zip(*batch)
        return np.array(states), np.array(actions), np.array(rewards), 
               np.array(next_states), np.array(dones)

 

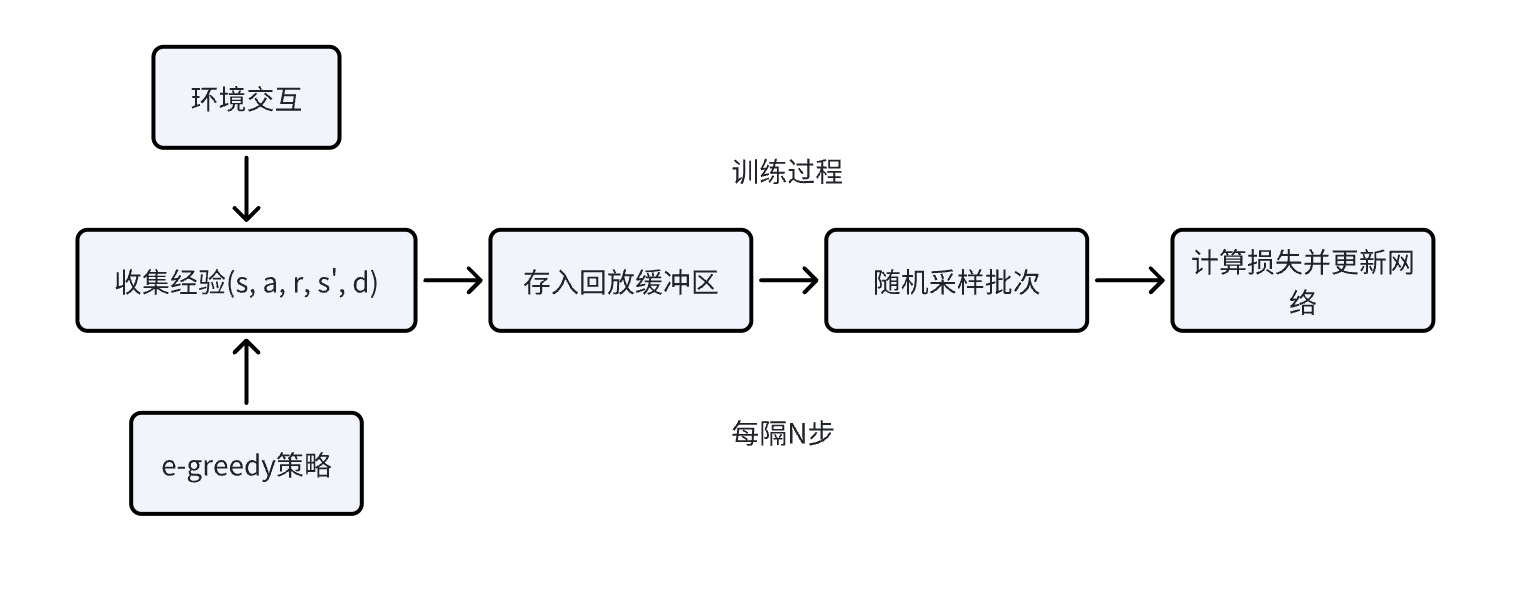
经验回放与e-greedy采样的关系：

1. 观察当前状态s
2. 使用e-greedy策略选择动作a执行动作a，获得(r, s', done)
3. 将经验(s, a, r, s', done)存入回放缓冲区
4. 从缓冲区随机采样一个批次
5. 用采样的批次更新神经网络
6. 定期更新目标网络
7. s'->s，进入下一个时间步，继续循环

代码：

# 在一个训练循环中
for episode in range(num_episodes):
    state = env.reset()
    done = False
    
    while not done:
        # ========== ε-greedy 部分 ==========
        # 选择动作（总是使用ε-greedy）
        if np.random.rand() <= epsilon:
            action = env.action_space.sample()  # 探索
        else:
            action = np.argmax(dqn.predict(state))  # 利用
        
        # 执行动作
        next_state, reward, done, _ = env.step(action)
        
        # ========== 经验回放 部分 ==========
        # 1. 存储经验
        replay_buffer.add(state, action, reward, next_state, done)
        
        # 2. 采样训练（如果缓冲区足够）
        if len(replay_buffer) > batch_size:
            batch = replay_buffer.sample(batch_size)
            dqn.train(batch)  # 训练网络
        
        # 3. 衰减ε
        epsilon = max(epsilon_min, epsilon * epsilon_decay)
        
        state = next_state

 

4.2 目标网络

目标网络是DQN算法中第二个关键创新点（第一个是经验回放），它解决了深度强化学习中的“移动目标问题”。在标准的 Q 学习更新中，我们同时使用同一个网络来计算当前 Q(s,a)值，计算目标 Q(s',a'｜θ): r + γ * max_a' Q(s', a'; θ)。在一个时间步（t0->t1->t2....tn）里面，目标值在学习过程中不断变化。example,

假设 Q(s,a; θ) = θ, max Q(s',a'; θ) = -θ + 10, 计算梯度，

 

$$\displaystyle{\displaylines{L(\theta)=\frac{1}{2}(target-Q(s,a))^{2}}}$$

$$\displaystyle{\displaylines{target=r+\gamma*max(Q(s',a'))}}$$

$$\displaystyle{\displaylines{\nabla L(\theta)=(target-Q)*(-\gamma-1)}}$$

 

设

• θ = 5 （当前参数）
• r = 1
• γ = 0.9
• max Q(s',a') = -θ + 10 = -5 + 10 = 5

可得

• Q(s,a) = θ = 5
• target = 1 + 0.9 * 5 = 1 + 4.5 = 5.5
• Diff = target - Q = 0.5
• ∇L(θ) = -0.95

根据 diff 我们要增加目标值，但是梯度为负，意味着我们要减少 θ，这两个结论相互矛盾。原因：

1. 观测序列有相关性 （使用经验回放机制解决）
2. 对 Q 值微小的更新可能显著改变策略，这会改变后续数据分布
3. Action value （Q 值）与目标值存在相关性 （固定 target）

 

4.3 DQN 例子

Cart-Pole 问题。一个平衡杆在 Cart 车上保持平衡。

 

代码来自 deep seek

import random
from collections import deque

import gymnasium as gym  # 强化学习环境库
import matplotlib.pyplot as plt  # 绘图库
import numpy as np
import torch
import torch.nn as nn  # 神经网络模块
import torch.nn.functional as F  # 神经网络函数
import torch.optim as optim  # 优化器

# 设置随机种子 - 确保实验可重复
SEED = 42
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)

# 检查是否有GPU可用，如果有则使用GPU加速计算
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备: {device}")



# ========== 1. 定义Q网络 ==========
class QNetwork(nn.Module):
    """深度Q网络：用于近似Q值函数"""
    def __init__(self, state_size, action_size):
        """
        初始化Q网络
        Args:
            state_size: 状态空间维度
            action_size: 动作空间大小
        """
        super(QNetwork, self).__init__()
        # 三层全连接神经网络
        self.fc1 = nn.Linear(state_size, 64)  # 输入层->隐藏层1
        self.fc2 = nn.Linear(64, 64)  # 隐藏层1->隐藏层2
        self.fc3 = nn.Linear(64, action_size)  # 隐藏层2->输出层（每个动作的Q值）

    def forward(self, x):
        """前向传播"""
        x = F.relu(self.fc1(x))  # ReLU激活函数
        x = F.relu(self.fc2(x))
        return self.fc3(x)  # 输出每个动作的Q值（未激活）


# ========== 2. 定义经验回放缓冲区 ==========
class ReplayBuffer:
    """经验回放缓冲区：存储和采样经验"""
    def __init__(self, capacity):
        """
        初始化经验池
        Args:
            capacity: 缓冲区最大容量
        """
        self.buffer = deque(maxlen=capacity)  # 使用双端队列，自动移除旧经验

    def push(self, state, action, reward, next_state, done):
        """存储一条经验（state, action, reward, next_state, done）"""
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        """随机采样一批经验"""
        batch = random.sample(self.buffer, batch_size)
        # 解压批处理数据
        states, actions, rewards, next_states, dones = zip(*batch)

        # 转换为PyTorch张量并移到指定设备
        return (
            torch.FloatTensor(np.array(states)).to(device),  # 状态
            torch.LongTensor(actions).unsqueeze(1).to(device),  # 动作，添加维度
            torch.FloatTensor(rewards).unsqueeze(1).to(device),  # 奖励
            torch.FloatTensor(np.array(next_states)).to(device),  # 下一状态
            torch.FloatTensor(dones).unsqueeze(1).to(device)  # 终止标志
        )

    def __len__(self):
        """返回缓冲区当前大小"""
        return len(self.buffer)


# ========== 3. 定义DQN智能体 ==========
class DQNAgent:
    """DQN智能体：包含学习算法的核心逻辑"""
    def __init__(self, state_size, action_size):
        """
        初始化智能体
        Args:
            state_size: 状态空间维度
            action_size: 动作空间大小
        """
        self.state_size = state_size
        self.action_size = action_size

        # 超参数
        self.buffer_size = 10000  # 经验回放缓冲区大小
        self.batch_size = 64  # 每次训练的批量大小
        self.gamma = 0.99  # 折扣因子（未来奖励的重要性）
        self.learning_rate = 0.001  # 学习率
        self.tau = 0.001  # 目标网络软更新参数（较小值表示目标网络更新慢）

        # 创建主Q网络和目标Q网络
        self.q_network = QNetwork(state_size, action_size).to(device)  # 主网络
        self.target_network = QNetwork(state_size, action_size).to(device)  # 目标网络
        self.target_network.load_state_dict(self.q_network.state_dict())  # 复制权重

        # 优化器：Adam优化器用于更新主网络
        self.optimizer = optim.Adam(self.q_network.parameters(), lr=self.learning_rate)

        # 经验回放缓冲区
        self.memory = ReplayBuffer(self.buffer_size)

        # 训练步数计数器
        self.steps = 0
        self.update_freq = 4  # 每4步更新一次网络

    def select_action(self, state, epsilon):
        """
        ε-greedy策略选择动作
        Args:
            state: 当前状态
            epsilon: 探索率
        Returns:
            action: 选择的动作
        """
        if random.random() < epsilon:
            # 探索：以epsilon概率随机选择动作
            return random.randrange(self.action_size)
        else:
            # 利用：以1-epsilon概率选择Q值最大的动作
            state = torch.FloatTensor(state).unsqueeze(0).to(device)  # 添加批次维度
            with torch.no_grad():  # 不计算梯度（评估阶段）
                q_values = self.q_network(state)  # 获取所有动作的Q值
            return q_values.argmax().item()  # 返回Q值最大的动作索引

    def store_experience(self, state, action, reward, next_state, done):
        """存储经验到回放缓冲区"""
        self.memory.push(state, action, reward, next_state, done)

    def learn(self):
        """执行一次学习步骤（更新Q网络）"""
        # 如果缓冲区中经验不足，不进行学习
        if len(self.memory) < self.batch_size:
            return

        # 从缓冲区采样一批经验
        states, actions, rewards, next_states, dones = self.memory.sample(self.batch_size)

        # 计算当前Q值：主网络对当前状态-动作对的评估
        # gather(1, actions): 选择执行的动作对应的Q值
        current_q = self.q_network(states).gather(1, actions)

        # 计算目标Q值：Bellman方程
        with torch.no_grad():  # 目标网络不需要梯度
            # 计算下一状态的最大Q值
            next_q = self.target_network(next_states).max(1, keepdim=True)[0]
            # Bellman方程: target = reward + γ * max Q(next_state) * (1-done)
            # (1-dones)确保终止状态的目标值为reward
            target_q = rewards + (self.gamma * next_q * (1 - dones))

        # 计算均方误差损失
        loss = F.mse_loss(current_q, target_q)

        # 反向传播
        self.optimizer.zero_grad()  # 清空梯度
        loss.backward()  # 反向传播计算梯度

        # 梯度裁剪：防止梯度爆炸
        torch.nn.utils.clip_grad_norm_(self.q_network.parameters(), 1.0)

        # 更新主网络参数
        self.optimizer.step()

        # 软更新目标网络参数
        # 目标网络参数 = τ * 主网络参数 + (1-τ) * 目标网络参数
        for target_param, param in zip(self.target_network.parameters(), self.q_network.parameters()):
            target_param.data.copy_(self.tau * param.data + (1.0 - self.tau) * target_param.data)

        return loss.item()  # 返回损失值用于记录

    def train_step(self, state, action, reward, next_state, done):
        """单步训练：存储经验并定期学习"""
        # 存储经验
        self.store_experience(state, action, reward, next_state, done)

        # 增加步数
        self.steps += 1

        # 定期学习（每update_freq步）
        if self.steps % self.update_freq == 0:
            loss = self.learn()
            return loss

        return None


# ========== 4. 训练函数 ==========
def train_dqn(env_name="CartPole-v1", episodes=500, max_steps=500):
    """训练DQN智能体"""
    print("开始训练DQN...")
    print(f"环境: {env_name}")
    print("=" * 50)

    # 创建环境
    env = gym.make(env_name)

    # 获取状态和动作空间信息
    state_size = env.observation_space.shape[0]  # 状态向量维度
    action_size = env.action_space.n  # 离散动作数量

    print(f"状态空间维度: {state_size}")
    print(f"动作空间大小: {action_size}")
    print("=" * 50)

    # 创建智能体
    agent = DQNAgent(state_size, action_size)

    # 训练指标
    scores = []  # 每回合得分（累积奖励）
    epsilons = []  # 探索率记录
    losses = []  # 损失记录

    # ε-greedy参数：探索率衰减
    eps_start = 1.0  # 初始探索率
    eps_end = 0.01  # 最小探索率
    eps_decay = 0.995  # 衰减率（每回合乘以这个值）

    epsilon = eps_start

    # 训练循环
    for episode in range(1, episodes + 1):
        # 重置环境，获取初始状态
        state, _ = env.reset()
        episode_score = 0  # 本回合累积奖励
        episode_losses = []  # 本回合损失

        # 回合内的每一步
        for step in range(max_steps):
            # 使用ε-greedy策略选择动作
            action = agent.select_action(state, epsilon)

            # 执行动作，获取环境反馈
            next_state, reward, terminated, truncated, _ = env.step(action)
            done = terminated or truncated  # 回合是否结束

            # 智能体学习
            loss = agent.train_step(state, action, reward, next_state, done)
            if loss is not None:
                episode_losses.append(loss)

            # 更新状态和得分
            state = next_state  # 转移到下一状态
            episode_score += reward  # 累积奖励

            if done:  # 如果回合结束，跳出循环
                break

        # 记录本回合数据
        scores.append(episode_score)
        epsilons.append(epsilon)

        if episode_losses:
            losses.append(np.mean(episode_losses))

        # 衰减探索率：随时间减少探索，增加利用
        epsilon = max(eps_end, epsilon * eps_decay)

        # 定期打印进度（每20回合）
        if episode % 20 == 0 or episode == 1:
            # 计算最近20回合的平均得分
            avg_score = np.mean(scores[-20:]) if len(scores) >= 20 else np.mean(scores)
            avg_loss = np.mean(losses[-20:]) if losses else 0
            print(f"回合 {episode:3d} | "
                  f"得分: {episode_score:4.0f} | "
                  f"平均得分: {avg_score:6.2f} | "
                  f"ε: {epsilon:.3f} | "
                  f"损失: {avg_loss:.4f}")

        # 提前停止条件：如果连续100回合平均得分达到195（CartPole解决标准）
        if len(scores) >= 100 and np.mean(scores[-100:]) >= 195:
            print(f"\n环境在 {episode} 回合解决! 平均得分: {np.mean(scores[-100:]):.2f}")
            break

    # 关闭环境
    env.close()

    print("训练完成!")
    print(f"最终平均得分: {np.mean(scores[-100:]):.2f}")

    return agent, scores, epsilons, losses


# ========== 5. 可视化训练结果 ==========
def plot_results(scores, epsilons, losses):
    """绘制训练结果图表"""
    fig, axes = plt.subplots(3, 1, figsize=(12, 10))

    # 1. 得分曲线
    axes[0].plot(scores, alpha=0.6, color='blue')
    axes[0].set_xlabel('回合')
    axes[0].set_ylabel('得分')
    axes[0].set_title('DQN训练得分')
    axes[0].grid(True, alpha=0.3)

    # 绘制移动平均线（窗口大小=20），平滑曲线
    if len(scores) >= 20:
        moving_avg = np.convolve(scores, np.ones(20) / 20, mode='valid')
        axes[0].plot(range(19, len(scores)), moving_avg, color='red', linewidth=2, label='20回合移动平均')
        axes[0].legend()

    # 2. 探索率衰减
    axes[1].plot(epsilons, color='green')
    axes[1].set_xlabel('回合')
    axes[1].set_ylabel('探索率 (ε)')
    axes[1].set_title('探索率衰减')
    axes[1].grid(True, alpha=0.3)

    # 3. 损失曲线
    if losses:
        axes[2].plot(losses, color='orange')
        axes[2].set_xlabel('回合')
        axes[2].set_ylabel('损失')
        axes[2].set_title('训练损失')
        axes[2].grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig('dqn_training_results.png', dpi=100, bbox_inches='tight')
    plt.show()

    # 打印统计信息
    print("\n" + "=" * 50)
    print("训练统计信息:")
    print(f"总回合数: {len(scores)}")
    print(f"平均得分: {np.mean(scores):.2f}")
    print(f"最高得分: {np.max(scores)}")
    print(f"最低得分: {np.min(scores)}")
    print(f"最后100回合平均得分: {np.mean(scores[-100:]):.2f}")
    print("=" * 50)


# ========== 6. 测试训练好的智能体 ==========
def test_agent(agent, env_name="CartPole-v1", episodes=10, render=True):
    """测试训练好的智能体"""
    print(f"\n开始测试智能体 ({episodes}个回合)...")

    # 创建测试环境
    if render:
        env = gym.make(env_name, render_mode='human')  # 可视化模式
    else:
        env = gym.make(env_name)

    test_scores = []

    for episode in range(1, episodes + 1):
        state, _ = env.reset()
        episode_score = 0
        done = False

        while not done:
            # 测试时使用完全贪婪策略（ε=0）
            action = agent.select_action(state, epsilon=0)
            state, reward, terminated, truncated, _ = env.step(action)
            done = terminated or truncated
            episode_score += reward

            if render:
                env.render()  # 显示环境

        test_scores.append(episode_score)
        print(f"测试回合 {episode}: 得分 = {episode_score}")

    env.close()

    print(f"\n测试结果:")
    print(f"平均得分: {np.mean(test_scores):.2f}")
    print(f"最高得分: {np.max(test_scores)}")
    print(f"最低得分: {np.min(test_scores)}")

    return test_scores


# ========== 7. 主程序 ==========
if __name__ == "__main__":
    print("=" * 50)
    print("DQN (深度Q网络) 示例")
    print("解决CartPole平衡问题")
    print("=" * 50)
    print()

    # 选择运行模式
    print("请选择运行模式:")
    print("1. 训练新模型")
    print("2. 快速演示（少量回合）")
    mode = input("输入选择 (1 或 2): ").strip()

    if mode == '1':
        # 训练模式：完整训练
        print("\n开始完整训练（约500回合）...")
        envName = 'CartPole-v1'
        agent, scores, epsilons, losses = train_dqn(
            env_name=envName,
            episodes=500,
            max_steps=500
        )

        # 绘制结果
        plot_results(scores, epsilons, losses)

        # 测试智能体
        test_mode = input("\n是否测试智能体？(y/n): ").strip().lower()
        if test_mode == 'y':
            test_agent(agent, env_name=envName, episodes=10, render=True)

    elif mode == '2':
        # 快速演示模式：少量训练回合
        print("\n开始快速演示（50回合）...")
        agent, scores, epsilons, losses = train_dqn(
            env_name="CartPole-v1",
            episodes=50,
            max_steps=200
        )

        # 绘制结果
        plot_results(scores, epsilons, losses)

    else:
        # 默认演示：随机策略
        print("\n默认运行快速演示...")

        # 创建环境
        env = gym.make("CartPole-v1")
        state_size = env.observation_space.shape[0]
        action_size = env.action_space.n

        # 创建智能体（未训练，只演示随机策略）
        agent = DQNAgent(state_size, action_size)

        print("\n演示随机策略（未训练）:")
        for episode in range(3):
            state, _ = env.reset()
            done = False
            score = 0

            while not done:
                action = agent.select_action(state, epsilon=1.0)  # 完全随机
                state, reward, terminated, truncated, _ = env.step(action)
                done = terminated or truncated
                score += reward

            print(f"回合 {episode + 1}: 得分 = {score}")

        env.close()

        print("\n建议运行模式1进行完整训练！")